It so happened that over the past six months I was able to meet a few simple (in the sense of the rules) and somewhat similar board games. The first in this series was Set, then Barabashka, and in the summer we played Dobl. I’ll say right away that all the games listed are quite fascinating, however, this post will, of course, not be about that. The fact is that after a while (in other words, having played enough) I was interested in the ideas underlying these games, and which turned out to be closely connected with combinatorics. In this post we will talk about the most simple (in my opinion) game - “Barabashka”, which, by the way, in the original version has the more euphonious name “Geistesblitz” (it is insight).

Rules of the game

So, what is the game. There are 5 objects, each of which, conditionally speaking, is characterized by shape and color (ie, two categories) - a white drumstick, a red chair, a blue book, a green bottle and a gray mouse.
')


In addition, there are a number of cards, each of which shows two objects that have a different shape and a different color (but from the above-listed shapes and colors). On some cards there are items that exactly match those of these items. On any card in at least one item the color does not match the form (for example, a red bottle).



The goal of the game is that for a given card, as soon as possible, identify an object that a) is either present in the correct form on the card (the form and color match), b) or is completely absent (there is neither the form of this object nor its colors).



In the first example, we have a white drum, we have to grab it, in the second example, our choice is a bottle, because there is no bottle on the card (as a form) and no green (it's easy to check that in this case the bottle is the only option as some categories of all the remaining items on the card are present).

Actually all the rules. The game itself is designed for several players, each plays for itself, the goal is to collect as many cards as possible (who first grabbed the right thing, and the card). Warning: do not play with people with long nails, possibly getting stab-cut wounds!

Number of cards

The first question that interested me is how many different cards are possible in this game. Pure combinatorics! What is nice, this problem is solved quite easily. To begin with, we note that we have two types of cards, let's call them correct (they have the right item on them) and wrong ones (there is no necessary item on such cards). Calculate separately the number of those and others.

Let's start with the right ones. The first item on the correct card can be selected in five ways (from the five available items). The second object is chosen smarter - first, we will choose its form (four options, one form is already occupied by the first object), then color (three options, one color is occupied by the first object, the second is occupied by the object, the form from which we took in the second step). Thus, according to the work rule , we get the total number of correct cards 5 * 4 * 3 = 60.

Wrong cards are considered similar. First, choose the shape of the first item (5 variants), then its color (4 variants). Then we choose the shape of the second item (3 variants) and its color (2 variations). There is just one uncovered item - the purpose of this card. Apply the rule of the product, we get 5 * 4 * 3 * 2 = 120 options. But this is the wrong answer - a set of items on the card is unordered , and we counted the number of ordered sets. To get the correct answer, 120 must be divided into 2 — the number of permutations of two elements (card “red bottle and white chair” = card “white chair and red bottle”). Thus, we get 120/2 = 60 wrong cards.

We summarize (i.e., apply the sum rule ) and get the answer: 120 cards for the game. We count the cards in the game - 60 pieces. Or an error in the calculations, or a shortage. A simple investigation revealed the fact of the shortage - for each of the five subjects there are six correct and six incorrect cards, but there should be 12 and 12. Moreover, no logic was found in the selection of cards (most likely the random choice).

Generalization

We reformulate slightly the problem. There are N items, each of which is described by k categories, and there are Q cards, each of which shows n items (in the above case N = 5, k = 2, n = 2 and Q = 120). There are limitations - the cards can be correct (in the above sense) and wrong. In any case, on each card, none of the kN possible signs are repeated (for example, all colors are different and all forms are different). In addition, each item is either fully depicted on the card, or there is no more than one sign from it: for example, there is no card with a white bottle and a red drum in the “Drumstick” (two signs from one item), since For such a card, there are two choices - a gray mouse or a blue book. The only and natural question that arises in such a generalized formulation is what is the relationship between the variables N, k, n, and Q?

First, it is easy to establish how N, k and n are related. Consider the wrong cards. Each such card shows n items, so there are exactly kn signs on it that define kn items (all signs are different, no two belong to the same item). Since such a card must correspond to a single object that is not included in it, we obtain the required number of objects kn + 1. Note that this number allows you to make and correct cards (on each correct card there are 1 + (n-1) k items in one form or another). Thus, N = kn + 1. It is easy to verify that the formula is true for the case considered above, n = k = 2 and N = 5. Imagine the dependency found as a table (the cell corresponding to the Barabashka game is highlighted in red):



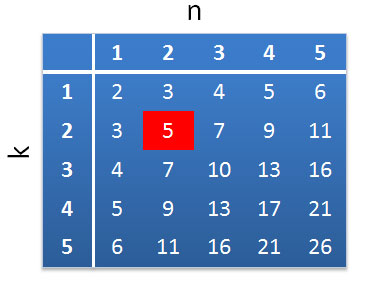
What do these numbers mean? Suppose we want to create an expanded (supercomplicated) version of the game, in which on each card there will be n = 5 items, and each item will be described by k = 5 categories. We get N = 26. This means that for each category you will need to come up with 26 of its values ​​(attributes). Those. if the category is a color, then 26 well-distinguished colors should be identified. Not an easy task ... Therefore, possible extensions of the game are most likely limited to the area near the upper left corner of the table. By the way, seemingly trivial cases n = 1 or k = 1 also have the right to life (although, most likely, in these cases a good reaction will be the main thing).

We now calculate the number of Q cards in the expanded (parameterized) version of the game. Using the above technique, we find the number of correct N! / K! / (N-1) cards! and the number of incorrect cards N! / n !, adding and simplifying, we get the result

.

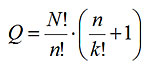The formula works for n = k = 2, and has also been tested for smaller values ​​of these parameters. However, in the case of n = k = 1, it lies slightly, since in this case, the correct card for one item coincides with the wrong card for another item (i.e., any choice will be winning), so the result must be divided by 2. In all other cases, such collisions do not occur. For the case n = k = 3, the formula gives the number Q = 907200. If each card is one-tenth of a millimeter thick, the full stack will be almost 90 meters high!

Realization of the case n = k = 3

After I figured out all this kitchen, it was decided to create a simple prototype demonstration of an expanded version of the game for all values ​​of n and k from 1 to 3. However, when it came to programming itself, my enthusiasm subsided a bit and I decided to limit myself to the case n = k = 3 (N = 10). So this is just a demonstration for the article, it was decided not to bother with graphics, but to make a text version of the game almost. So, three categories are letters (from A to J), numbers (from 0 to 9 - very well, that we have a decimal number system) and special characters (percentages, dollars, etc.) Thus, each “subject” - this is a set (unordered) of three characters (letter + digit + special character): A0%, B1 $, etc. The game is designed for one player, who is given 100 seconds to guess objects. The correct choice of the subject adds 1 to the score, the wrong one reduces the score by 1 (but only to zero). The game is implemented in HTML + JS and posted here (tested only under chrome). The interface is very simple:



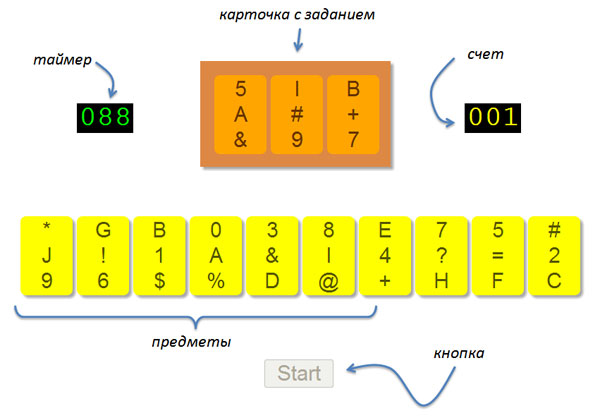
The top row shows a card with three items, the bottom row shows the items themselves. It is necessary to choose from the bottom row an item that is either on the card (all three symbols match), or an item that has no symbol on the card. In this example, the correct choice is a card with the letter G. A small obfuscation (mixing “objects” and symbols in “objects”) is used to complicate the game. Note that the original version of “Barabashka” is also obfuscated - the objects have different sizes and are differently located on the card (in addition, real objects are constantly mixed by the players themselves during the game). Good luck to those who dare to play (my record so far - about 6 guessed objects)!

Thank you all for your attention!

PS: And what about the orthogonal polynomials, the attentive reader will ask. Honestly, I do not know! But if we take the formula for Q and substitute k = 2 into it, we get a numerical sequence that starts like this: 1, 9, 120, 2100, etc. There is such a great site - a dictionary of integer sequences, which allows you to find the sequence itself (like the game “Guess the melody”) by several elements of the sequence. I drove in there the found numbers and the only sequence was found that is connected just with the coefficients of orthogonal polynomials ... The test showed that the formulas (mine and them) are identical. I was not lazy, I found and downloaded the original article , my numbers were the third most significant coefficients in the polynomials obtained in some way in the process of the inverse Laplace transform . Unfortunately, I failed to understand what connection between these polynomials and Barabashka ...