Homomorphic DIY Encryption
Good day, dear readers. Those of you who are interested in cryptography probably know what homomorphic encryption is and what it is for. For those who do not yet understand what it is about, I will give a definition from the Russian-language Wikipedia:
Homomorphic encryption is a cryptographic system that allows you to perform certain mathematical operations with plaintext by performing operations with encrypted text.
For a long time, a fully homomorphic cryptosystem remained for all cryptographers of the world a holy Grail, an unattainable ideal. And in 2009, Craig Gentry in his dissertation for the first time described a fully working homomorphic encryption scheme.
You will find several mathematical details of the Gentry idea as well as an example of its algorithm implementation under the cat.
Any standard encryption system can be described by three algorithms.
The homomorphic cryptosystem in addition to the three algorithms listed above includes the Eval () computation algorithm.
Schematically, the Eval algorithm can be represented as follows:
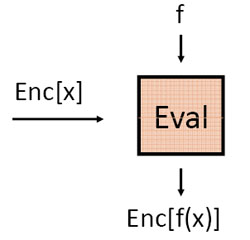
The algorithm receives the encrypted message Enc (M) and a certain mathematical function f () . The result of the algorithm is another encrypted message Enc (M 2 ) , with M 2 = f (M) .
')
A homomorphic encryption scheme is considered correct if for any pair of keys SK, PK, for any function f () , for any set of ciphertexts C = {c 1 , c 2 , .., c n } and a set of clear texts M = {m 1 , m 2 , .., m n } such that C = Enc (M) the following condition is satisfied:
If r = Eval (PK, C, f) then decypt (SK, r) = f (m 1 , m 2 , .., m n )
The scheme proposed by Gentry meets this condition and therefore it can be called completely homomorphic.
We describe the encryption scheme itself applicable for the data presented in numerical form.
Keygen
Private key: a large even number N.
Public key: a set of large numbers {a 1 , a 2 , .., a i } such that a i mod N = 2e i , where e i numbers are much smaller than N.
Encrypt
From the public key, we generate a random number b = random-subset-sum {a i } . In order to encrypt 1 bit of information, m ∈ {0,1}, we calculate
C = b + m
Decrypt
To decrypt we calculate
With mod N = m + 2 * P e i
2 * e i is called noise, if this expression in the process of calculations becomes more than the number N , then decoding will be impossible.
After modulo two, we get the original message m .
Eval
To make addition or multiplication of the ciphered elements without decoding them, it is rather simple to add or multiply ciphertexts.
Despite the fact that this scheme is absolutely working, it is not of great interest, because it can only encrypt 1 bit of information. In order to work with large numbers, we slightly modify the algorithm.
Let's build a scheme that would allow us to encrypt numbers no more than 15.
Keygen
Private key: a large number N , such that GCD (N, 15) = 1 .
Public key: a set of large numbers {a 1 , a 2 , .., a i } such that a i mod N = 15e i , where e i numbers are much smaller than N.
Encrypt
From the public key, we generate a random number b = random-subset-sum {a i } . In order to encrypt a number from 0 to 15, we calculate
C = b + m
Decrypt
To decrypt we calculate
With mod N = m + 15 * P e i
After modulo 15, we get the original message m .
Below is the part of the code containing the key generation, encryption and decryption functions.
Download the source code of the program that implements the encryption of numbers up to 1000 from here .
In conclusion, it is worth noting that the cryptosystem described in this topic is nothing more than a prototype, the main purpose of which is to acquaint those interested in the principle of operation of the homomorphic cryptosystem. Real homomorphic schemes do not work with integers, but with polynomial rings, and in them, after each calculation, they are reduced to absolute values in order to reduce noise and not make decoding impossible.
Homomorphic encryption is a cryptographic system that allows you to perform certain mathematical operations with plaintext by performing operations with encrypted text.
For a long time, a fully homomorphic cryptosystem remained for all cryptographers of the world a holy Grail, an unattainable ideal. And in 2009, Craig Gentry in his dissertation for the first time described a fully working homomorphic encryption scheme.
You will find several mathematical details of the Gentry idea as well as an example of its algorithm implementation under the cat.
Homomorphic encryption.
Any standard encryption system can be described by three algorithms.
- Key Generation KeyGen ()
- Encryption Encypt ()
- Decrypt Decrypt ()
The homomorphic cryptosystem in addition to the three algorithms listed above includes the Eval () computation algorithm.
Schematically, the Eval algorithm can be represented as follows:

The algorithm receives the encrypted message Enc (M) and a certain mathematical function f () . The result of the algorithm is another encrypted message Enc (M 2 ) , with M 2 = f (M) .
')
A homomorphic encryption scheme is considered correct if for any pair of keys SK, PK, for any function f () , for any set of ciphertexts C = {c 1 , c 2 , .., c n } and a set of clear texts M = {m 1 , m 2 , .., m n } such that C = Enc (M) the following condition is satisfied:
If r = Eval (PK, C, f) then decypt (SK, r) = f (m 1 , m 2 , .., m n )
The scheme proposed by Gentry meets this condition and therefore it can be called completely homomorphic.
Gentry scheme with numbers
We describe the encryption scheme itself applicable for the data presented in numerical form.
Keygen
Private key: a large even number N.
Public key: a set of large numbers {a 1 , a 2 , .., a i } such that a i mod N = 2e i , where e i numbers are much smaller than N.
Encrypt
From the public key, we generate a random number b = random-subset-sum {a i } . In order to encrypt 1 bit of information, m ∈ {0,1}, we calculate
C = b + m
Decrypt
To decrypt we calculate
With mod N = m + 2 * P e i
2 * e i is called noise, if this expression in the process of calculations becomes more than the number N , then decoding will be impossible.
After modulo two, we get the original message m .
Eval
To make addition or multiplication of the ciphered elements without decoding them, it is rather simple to add or multiply ciphertexts.
Despite the fact that this scheme is absolutely working, it is not of great interest, because it can only encrypt 1 bit of information. In order to work with large numbers, we slightly modify the algorithm.
Let's build a scheme that would allow us to encrypt numbers no more than 15.
Keygen
Private key: a large number N , such that GCD (N, 15) = 1 .
Public key: a set of large numbers {a 1 , a 2 , .., a i } such that a i mod N = 15e i , where e i numbers are much smaller than N.
Encrypt
From the public key, we generate a random number b = random-subset-sum {a i } . In order to encrypt a number from 0 to 15, we calculate
C = b + m
Decrypt
To decrypt we calculate
With mod N = m + 15 * P e i
After modulo 15, we get the original message m .
C # implementation
Below is the part of the code containing the key generation, encryption and decryption functions.
// , k- // private BigInteger[] PublicKeyGenerate(BigInteger N, int k) { Random r = new Random(); byte[] rand = new byte[16]; BigInteger rem; for (int i = 0; i < 100; i++) { r.NextBytes(rand); PK[i] = new BigInteger(rand); PK[i] = (BigInteger.Abs(PK[i]) * N) + (k* r.Next(10, 100)); rem = BigInteger.Remainder(PK[i], N);; } return PK; } // , // M PK private BigInteger Encryption(BigInteger M, BigInteger[] PK) { BigInteger B = new BigInteger(0); BigInteger C = new BigInteger(0); Random r = new Random(); for (int i = 0; i < 100; i++) { if (r.Next(2) == 1) B = B + PK[i]; } C = M + B; return C; } // , C-, N- , //k- private BigInteger Decryption(BigInteger C, BigInteger N, int k) { BigInteger M = new BigInteger(0); M = BigInteger.Remainder(C, N); return BigInteger.Remainder(M, k); } Download the source code of the program that implements the encryption of numbers up to 1000 from here .
Conclusion
In conclusion, it is worth noting that the cryptosystem described in this topic is nothing more than a prototype, the main purpose of which is to acquaint those interested in the principle of operation of the homomorphic cryptosystem. Real homomorphic schemes do not work with integers, but with polynomial rings, and in them, after each calculation, they are reduced to absolute values in order to reduce noise and not make decoding impossible.
References to sources
Source: https://habr.com/ru/post/150067/
All Articles