Mathematical expressions in .NET (parsing, differentiation, simplification, fractions, compilation)
 Since school time, I was interested in an algorithm for deriving analytical derivatives and simplifying expressions. This task was relevant later in the university. It was then that I implemented it, but everything did not turn out the way I wanted: instead of IL code, I simply generated C # code in text form, the assemblies were not unloaded, and besides, it was not possible to derive derivatives in analytical form. However, then I decided to still implement such a library, since interest remained. It should be noted that there are a large number of such libraries on the Internet, but nowhere did I find the stage of compiling expressions into IL code, i.e. in essence, interpretation is performed everywhere, which is not as effective as compiling. Well, and besides, I was developing it purely for myself, for learning new technologies, especially not hoping that the result of my work might be needed anywhere. For impatient: source code , the program .
Since school time, I was interested in an algorithm for deriving analytical derivatives and simplifying expressions. This task was relevant later in the university. It was then that I implemented it, but everything did not turn out the way I wanted: instead of IL code, I simply generated C # code in text form, the assemblies were not unloaded, and besides, it was not possible to derive derivatives in analytical form. However, then I decided to still implement such a library, since interest remained. It should be noted that there are a large number of such libraries on the Internet, but nowhere did I find the stage of compiling expressions into IL code, i.e. in essence, interpretation is performed everywhere, which is not as effective as compiling. Well, and besides, I was developing it purely for myself, for learning new technologies, especially not hoping that the result of my work might be needed anywhere. For impatient: source code , the program .Used programs and libraries
- GOLD Parsing System - IDE for writing grammars and generating code for lexers and parsers for various languages (C, C #, Java, JavaScript, Objective-C, Perl, Python, Ruby, etc.). Based on LALR parsing.
- Visual studio 2010
- GOLD.Engine - assembly under .NET, connected to interact with the generated tables.
- NUnit - Open application testing unit for .NET environment.
- ILSpy - OpenSource disassembler for .NET.
Stages into which I broke the whole process:
- Building an expression tree
- Calculation of analytical derivative
- Simplification (simplification) of expression
- Processing of rational fractions
- Expression compilation
Building an expression tree
I chose the GOLD parser generator because I already have experience with ANTLR and wanted something new. Well, its advantages, compared with the others, you can see in this table . As you can see, when compared with ANTLR, then GOLD is based on the LALR algorithm, not LL . And this means that, in theory, the generated parser is faster and more powerful, but on the other hand, it cannot be debugged (in GOLD, the file in binary format is loaded), and if it could, it would not be obvious and inconvenient . Another big difference is the grammar assignment form: BNF , not EBNF . This means that the grammar written in this form has a slightly larger size due to the angle brackets, the definition sign and the absence of conditional entries and repetitions (in more detail in the wiki . And, for example, such a rule in EBNF as
ExpressionList = Expression { ',' Expression } will be rewritten in this form:
')
<ExpressionList> ::= <ExpressionList> ',' <Expression> | <Expression> So, the final grammar of mathematical expressions is as follows:
Grammar of Mathematical Expressions
"Name" = 'Mathematics expressions' "Author" = 'Ivan Kochurkin' "Version" = '1.0' "About" = '' "Case Sensitive" = False "Start Symbol" = <Statements> Id = {Letter}{AlphaNumeric}* Number1 = {Digit}+('.'{Digit}*('('{Digit}*')')?)? Number2 = '.'{Digit}*('('{Digit}*')')? AddLiteral = '+' | '-' MultLiteral = '*' | '/' <Statements> ::= <Statements> <Devider> <Statement> | <Statements> <Devider> | <Statement> <Devider> ::= ';' | '.' <Statement> ::= <Expression> '=' <Expression> | <Expression> <Expression> ::= <FuncDef> | <Addition> <FuncDef> ::= Id '(' <ExpressionList> ')' | Id '' '(' <ExpressionList> ')' | Id '(' <ExpressionList> ')' '' <ExpressionList> ::= <ExpressionList> ',' <Expression> | <Expression> <Addition> ::= <Addition> AddLiteral <Multiplication> | <Addition> AddLiteral <FuncDef> | <FuncDef> AddLiteral <Multiplication> | <FuncDef> AddLiteral <FuncDef> | <Multiplication> <Multiplication> ::= <Multiplication> MultLiteral <Exponentiation> | <Multiplication> MultLiteral <FuncDef> | <FuncDef> MultLiteral <Exponentiation> | <FuncDef> MultLiteral <FuncDef> | <Exponentiation> <Exponentiation> ::= <Exponentiation> '^' <Negation> | <Exponentiation> '^' <FuncDef> | <FuncDef> '^' <Negation> | <FuncDef> '^' <FuncDef> | <Negation> <Negation> ::= AddLiteral <Value> | AddLiteral <FuncDef> | <Value> <Value> ::= Id | Number1 | Number2 | '(' <Expression> ')' | '|' <Expression> '|' | '(' <Expression> ')' '' | '|' <Expression> '|' '' | Id '' Everything seems to be obvious in grammar, with the exception of the token: Number1 = {Digit} + ('.' {Digit} * ('(' {Digit} * ')')?)? This construction allows to parse lines of the following form: 0.1234 (56), which means a rational fraction: 61111/495000. I will tell you about the conversion of such a string into a fraction later.
So, after the compiled Grammar Table File has been generated and the parser class has been created, it is necessary to modify the latter in order to build a suitable AST tree. The framework of the parser class in this case is the .cs file in which the crawl cycle is written according to all the rules of grammar, exception handling in case of an incorrect sequence of tokens and other errors (by the way, GOLD also has different generators of such frameworks, and I chose Cook .NET ). So, in our case “suitable” means a tree consisting of nodes that can have types:
- Calculated is a node representing a calculated constant in a format acceptable for the compiler double , for example, "0.714285714285714", "0.122222222222222". For each such constant, a new object is created, even if they are the same.
- Value is the node representing the calculated constant in the rational fraction format, i.e. 1 is represented as "1/1", "0.1 (2)" - as "11/90", "0.1234" - as "617/5000". For each such constant, a new object is created, even if they are the same.
- Constant - a node that represents an undefined constant, for example, "a", "b", etc. If there are two such constants in the expression, then they point to one node.
- Variable - a node that represents a variable, for example, "x", "y", etc. If a certain variable occurs several times in an expression, then only one object is created for it, as well as for an undefined constant. It is important to understand that the distinction between a constant and a variable is important only at the stage of derivation of an analytical derivative, and in other cases this knowledge is not necessary.
- Function - the node representing the function, for example, "+", "sin", "^" and others. The only node that can have descendants.
All types of nodes are graphically represented in the figure:

From the grammar it is clear that the nodes of the obtained tree either have no children (for example, values or variables), or have from one to two children in the case of standard functions (for example, cos, addition, raising to a power). All other functions may have more arguments, but they were not considered.
Thus, all nodes (or rather nodes with functions) have from 0 to 2 children inclusive. This is true from a theoretical point of view. But in fact, I had to make the functions "+" and "*" have an unlimited number of children in order to facilitate the task of simplification, which will be discussed later. By the way, such binary operations as "-" and "/" also had to be abandoned for the same reasons (they were replaced by addition with negation of the right side and multiplication with inversion of the right side).
So, at the parsing stage, all nodes for each rule are dropped or extracted from a buffer called Nodes . Thus, at the end of the whole process, one or several functions with the right and left parts remain in this buffer. Also in the parsing process, in order for the addition and multiplication functions to be immediately created by multi-line functions, additional buffers ArgsCount and ArgsFuncTypes were used, storing the current number of arguments in the function and the type of the current function, respectively. Thus, for example, for the multiplication function, this code is used:
Processing the first multiplier:
// <Multiplication> ::= <Exponentiation> if (MultiplicationMultiChilds) PushFunc(KnownMathFunctionType.Mult); Processing the i-th factor:
// <Multiplication> ::= <Multiplication> MultLiteral <Exponentiation> // <Multiplication> ::= <Multiplication> MultLiteral <FuncDef> if (KnownMathFunction.BinaryNamesFuncs[r[1].Data.ToString()] == KnownMathFunctionType.Div) Nodes.Push(new FuncNode(KnownMathFunctionType.Exp, new MathFuncNode[] { Nodes.Pop(), new ValueNode(-1) })); ArgsCount[ArgsCount.Count - 1]++; Handling the last multiplier:
// <Addition> ::= <Multiplication> if (MultiplicationMultiChilds) PushOrRemoveFunc(KnownMathFunctionType.Mult); if (AdditionMultiChilds) PushFunc(KnownMathFunctionType.Add); From this code it can be seen that, for example, if there is no multiplication, then the last multiplication function with zero number of elements needs to be removed using PushOrRemoveFunc . Similar actions need to be carried out and for addition.
Processing functions of a single argument, binary functions, constants, variables and values is trivial, and all this can be found in MathExprParser.cs .
Calculation of analytical derivative
At this stage, you need to convert the function to its derivative.
As is known from the first stage, in the created expression tree there are only four types of nodes (the fifth one appears later). For them, we define the derivative:
- Value '= 0
- Constant '= 0
- Variable '= 1
- Function '= Derivatives [Function]
Let me explain: for a derivative of a function, it is necessary to take a previously prepared table value, and this causes certain difficulties, because there are also derivatives within this value, i.e. The process is recursive. You can see the full list of such implemented substitutions under the spoiler below.
Derivatives List
(f(x) ^ g(x))' = f(x) ^ g(x) * (f(x)' * g(x) / f(x) + g(x)' * ln(f(x)));"); neg(f(x))' = neg(f(x)');"); sin(f(x))' = cos(f(x)) * f(x)'; cos(f(x))' = -sin(f(x)) * f(x)'; tan(f(x))' = f(x)' / cos(f(x)) ^ 2; cot(f(x))' = -f(x)' / sin(f(x)) ^ 2; arcsin(f(x))' = f(x)' / sqrt(1 - f(x) ^ 2); arccos(f(x))' = -f(x)' / sqrt(1 - f(x) ^ 2); arctan(f(x))' = f(x)' / (1 + f(x) ^ 2); arccot(f(x))' = -f(x)' / (1 + f(x) ^ 2); sinh(f(x))' = f(x)' * cosh(x); cosh(f(x))' = f(x)' * sinh(x); arcsinh(f(x))' = f(x)' / sqrt(f(x) ^ 2 + 1); arcosh(f(x))' = f(x)' / sqrt(f(x) ^ 2 - 1); ln(f(x))' = f(x)' / f(x); log(f(x), g(x))' = g'(x)/(g(x)*ln(f(x))) - (f'(x)*ln(g(x)))/(f(x)*ln(f(x))^2); It should be noted that all derivatives are not written rigidly in the code, but can also be entered and parsed dynamically.
There is no addition and multiplication in this list because, as mentioned above, these are functions with several arguments. And in order to parse such rules, it would be necessary to still write a lot of code. For the same reasons, there is no composition of functions, i.e. (f (g (x))) '= f (g (x))' * g (x) ', but instead all functions are presented as function compositions.
Also, if a substitution in Derivatives (i.e., an undefined function) is not found for a function, then it is simply replaced with a function with a stroke: i.e. f (x) becomes f (x) '.
After the analytical derivative has been successfully obtained, the problem arises, which is that in the resulting expression there is a lot of "garbage", such as a + 0, a * 1, a * a ^ -1, etc., and also, the resulting expression can be calculated in a more optimal way. For example, even for a simple expression you get an ugly expression:
(x^2 + 2)' = 0 + 2 * 1 * x ^ 1 To eliminate such drawbacks, simplification is used.
Simplification (simplification) of expression
At this stage, unlike the step of calculating derivatives, I did not write down the rules of simplification in a separate place, for their subsequent analysis because the addition and multiplication functions are functions of several arguments, which is a certain difficulty in creating such rules in context of an iterative language.
At the beginning of the topic, I touched on the topic of why addition and multiplication are represented as n-ary functions. Imagine the situation shown in the picture below. Here we see that a and -a are reduced. But how to do it in the case of binary functions? To do this, we need to iterate over nodes a , b, and c , in order to later discover that a and -a are children of the same node, which means that they can be reduced with the node. But, of course, that sorting through trees is not such an easy task, since it is much easier to perform all the actions in a cycle with all the children at once, as shown in the figure on the right. By the way, this sort of search allows us to make mathematical properties of associativity and commutativity .
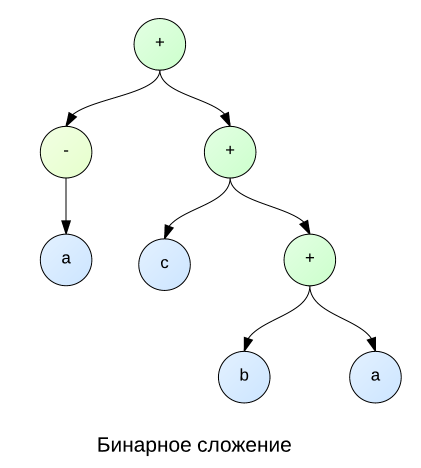 |  |
During the process of simplification, the problem arises of comparing two nodes, which, in turn, can be of one of four types. This is necessary, for example, in order to reduce expressions such as sin (x + y) and -sin (x + y). It is clear that it is possible to compare the nodes themselves and all their descendants by nodes. But the problem is that this method does not cope with the situation when the terms or factors are rearranged, for example, sin (x + y) and -sin (y + x). To resolve this problem, a preliminary sorting of the terms or factors for which the commutativity property is fulfilled (that is, for addition and subtraction) is used. The nodes are compared as shown in the picture below, i.e. values less than constants, constants less variables, etc. For functions, everything is a bit more complicated, since it is necessary to compare not only their names, but also the number of arguments and the arguments themselves.

Thus, after all the above-described transformations and iterations, the original expression is simplified quite well.
Processing of rational fractions
In the rational implementations I found there was no conversion of the usual string type, for example, 0.666666, into a fraction type with a specific numerator and denominator, i.e. in 2/3 with a certain accuracy. Then I decided to write my own implementation with a lot of options. The functions below can, for example, determine whether a number is purely irrational, or it has a period or finite fractional part and can be converted to rational, for example, sin (pi) to 0 with a certain accuracy. In general, for other details, see my response to stackoverflow.com . A brief graphic explanation of the method is presented in the figure below, and the code is shown in the listing below. It is worth noting that, nevertheless, the accuracy of standard mathematical functions and the double type are not enough for normal recognition of rational and real numbers, but theoretically everything works.
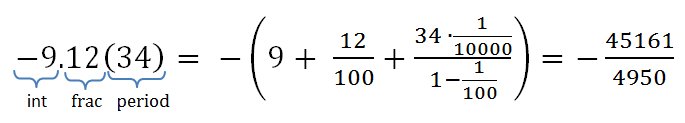
Convert decimal to fraction
/// <summary> /// Convert decimal to fraction /// </summary> /// <param name="value">decimal value to convert</param> /// <param name="result">result fraction if conversation is succsess</param> /// <param name="decimalPlaces">precision of considereation frac part of value</param> /// <param name="trimZeroes">trim zeroes on the right part of the value or not</param> /// <param name="minPeriodRepeat">minimum period repeating</param> /// <param name="digitsForReal">precision for determination value to real if period has not been founded</param> /// <returns></returns> public static bool FromDecimal(decimal value, out Rational<T> result, int decimalPlaces = 28, bool trimZeroes = false, decimal minPeriodRepeat = 2, int digitsForReal = 9) { var valueStr = value.ToString("0.0000000000000000000000000000", CultureInfo.InvariantCulture); var strs = valueStr.Split('.'); long intPart = long.Parse(strs[0]); string fracPartTrimEnd = strs[1].TrimEnd(new char[] { '0' }); string fracPart; if (trimZeroes) { fracPart = fracPartTrimEnd; decimalPlaces = Math.Min(decimalPlaces, fracPart.Length); } else fracPart = strs[1]; result = new Rational<T>(); try { string periodPart; bool periodFound = false; int i; for (i = 0; i < fracPart.Length; i++) { if (fracPart[i] == '0' && i != 0) continue; for (int j = i + 1; j < fracPart.Length; j++) { periodPart = fracPart.Substring(i, j - i); periodFound = true; decimal periodRepeat = 1; decimal periodStep = 1.0m / periodPart.Length; var upperBound = Math.Min(fracPart.Length, decimalPlaces); int k; for (k = i + periodPart.Length; k < upperBound; k += 1) { if (periodPart[(k - i) % periodPart.Length] != fracPart[k]) { periodFound = false; break; } periodRepeat += periodStep; } if (!periodFound && upperBound - k <= periodPart.Length && periodPart[(upperBound - i) % periodPart.Length] > '5') { var ind = (k - i) % periodPart.Length; var regroupedPeriod = (periodPart.Substring(ind) + periodPart.Remove(ind)).Substring(0, upperBound - k); ulong periodTailPlusOne = ulong.Parse(regroupedPeriod) + 1; ulong fracTail = ulong.Parse(fracPart.Substring(k, regroupedPeriod.Length)); if (periodTailPlusOne == fracTail) periodFound = true; } if (periodFound && periodRepeat >= minPeriodRepeat) { result = FromDecimal(strs[0], fracPart.Substring(0, i), periodPart); break; } else periodFound = false; } if (periodFound) break; } if (!periodFound) { if (fracPartTrimEnd.Length >= digitsForReal) return false; else { result = new Rational<T>(long.Parse(strs[0]), 1, false); if (fracPartTrimEnd.Length != 0) result = new Rational<T>(ulong.Parse(fracPartTrimEnd), TenInPower(fracPartTrimEnd.Length)); return true; } } return true; } catch { return false; } } public static Rational<T> FromDecimal(string intPart, string fracPart, string periodPart) { Rational<T> firstFracPart; if (fracPart != null && fracPart.Length != 0) { ulong denominator = TenInPower(fracPart.Length); firstFracPart = new Rational<T>(ulong.Parse(fracPart), denominator); } else firstFracPart = new Rational<T>(0, 1, false); Rational<T> secondFracPart; if (periodPart != null && periodPart.Length != 0) secondFracPart = new Rational<T>(ulong.Parse(periodPart), TenInPower(fracPart.Length)) * new Rational<T>(1, Nines((ulong)periodPart.Length), false); else secondFracPart = new Rational<T>(0, 1, false); var result = firstFracPart + secondFracPart; if (intPart != null && intPart.Length != 0) { long intPartLong = long.Parse(intPart); result = new Rational<T>(intPartLong, 1, false) + (intPartLong == 0 ? 1 : Math.Sign(intPartLong)) * result; } return result; } private static ulong TenInPower(int power) { ulong result = 1; for (int l = 0; l < power; l++) result *= 10; return result; } private static decimal TenInNegPower(int power) { decimal result = 1; for (int l = 0; l > power; l--) result /= 10.0m; return result; } private static ulong Nines(ulong power) { ulong result = 9; if (power >= 0) for (ulong l = 0; l < power - 1; l++) result = result * 10 + 9; return result; } Expression compilation
To convert the resulting semantic tree into IL code after the simplification stage, I used Mono.Cecil.
At the beginning of the process, an assembly, class and method are created in which commands will be written. Then for each FuncNode it is calculated how many times it occurs in the program. For example, if there is a function sin (x ^ 2) * cos (x ^ 2) , then in it the function of raising x to the power of 2 occurs twice, and the functions sin and cos - one at a time. Further, this information about the repetition of the calculations of functions is used as follows (that is, this way the second time, the calculations of the same function do not occur):
if (!func.Calculated) { EmitFunc(funcNode); func.Calculated = true; } else IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); After generating all this code, some more optimizations of the IL code are possible, as shown in the figure below.
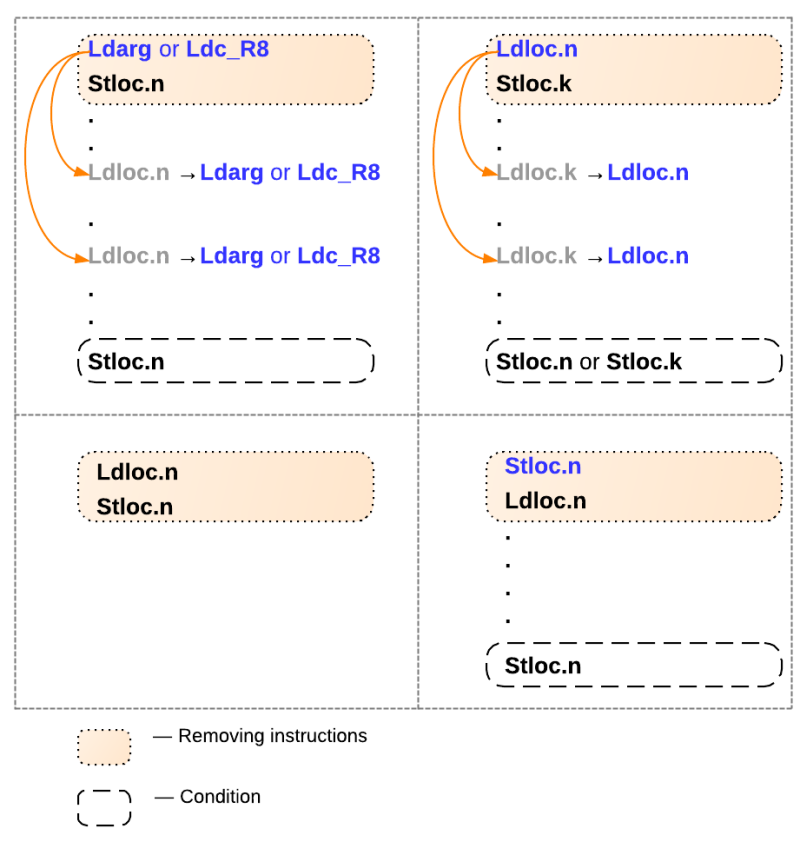
In this picture:
- Ldarg - The operation of loading a specific function argument to the stack.
- Ldc_R8 - Load a specific double value onto the stack.
- Stloc.n - Retrieving the last value from the stack and saving it to a local variable n .
- Ldloc.n - Putting local variable n on the stack.
Instructions in beige rectangles can be removed if certain conditions are met. For example, the case on the upper left image is described as follows: If the current instruction is loading an argument from a function or loading a constant, and the next instruction is saving it to a local variable n , then this block of instructions can be deleted by first replacing the loading instructions of the local variable n by loading function argument or constant loading. The replacement process is continued until the first save instruction in the local variable n . The other three cases are explained in a similar way. for example, the sequence Ldloc.n ; Stloc.n can be removed immediately.
It is worth noting that the optimization data is applicable in the case of absence of branching in the code, and this is obviously why (if not completely obvious, then I suggest reflecting). But since the code of mathematical functions and their derivatives cannot contain cycles in my case, it all works.
Quick exponentiation
I think that almost everyone knows about the algorithm of fast number exponentiation . But below is the compilation level of this algorithm:
Algorithm of quick exponentiation implemented in IL code
if (power <= 3) { IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); for (int i = 1; i < power; i++) { IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } } else if (power == 4) { IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } else { // result: funcNode.Number // x: funcNode.Number + 1 //int result = x; IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); power--; do { if ((power & 1) == 1) { IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); } if (power <= 1) break; //x = x * x; IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1)); IlInstructions.Add(new OpCodeArg(OpCodes.Mul)); IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number + 1)); power = power >> 1; } while (power != 0); } It is worth noting that the quick exponentiation algorithm is not the most optimal exponentiation algorithm. For example, the following is a multiplication of the same variables five times in two ways. Optimizations of the type x ^ 4 + x ^ 3 + x ^ 2 + x = x * (x * (x * (x + 1) + 1) + 1) are also not implemented by me.
- var t = a ^ 2; a * a * a * a * a * a = t ^ 2 * t is the usual “fast” algorithm.
- a * a * a * a * a * a = (a ^ 3) ^ 2 is the optimal “fast” algorithm.
By the way, it is also worth mentioning that for ordinary fixed double numbers, the result of multiplication for the above mentioned multiplications in different order will be different (i.e. (a ^ 2) ^ 2 * a ^ 2! = (A ^ 3) ^ 2 ). And because of this, some compilers do not optimize many similar expressions. On this occasion, there are interesting Q & A in stackoverlofw: Why doesn't GCC optimize a * a * a * a * a * a * a to (a * a * a) * (a * a * a)? and Why Math.Pow (x, 2) is not optimized x x neither compiler nor JIT? .
Optimization of local variables
As is known from the previous steps, local variables are used to store the result of all functions that occur more than 1 time in the original expression. To work with local variables, only two simple instructions are used: stloc and ldloc , which use one argument responsible for the number of this local variable. But if the number of a local variable is incremented every time there is a recurring result of the calculations (to create it), then there can be a lot of local variables. To level this problem, the compression algorithm for the life cycles of local variables was implemented, the process of which can be clearly seen in the figure below. As you can see, instead of 5 local variables in the expression, you can use only 3. However, this “greedy” algorithm is not the most optimal permutation, but it is quite suitable for the realizable problem.
 |  |
Compilation of undefined functions and their derivatives
In the developed library, you can use not only simple functions of one variable type f (x), but also others, such as f (x, a, b (x)), where a is an unknown constant, and b (x) is an unknown function transmitted as a delegate. As is known, the definition of the derivative of any function is as follows: b (x) '= (b (x + dx) - b (x)) / dx. And when the compilation module encounters an undefined function, it generates the following code:
ldarg.1 ldarg.0 callvirt TResult System.Func`2<System.Double,System.Double>::Invoke(T) ret The code for calculating the derivative of the undefined function (dx = 0.000001)
ldarg.1 ldarg.0 ldc.r8 1E-06 add callvirt TResult System.Func`2<System.Double,System.Double>::Invoke(T) ldarg.1 ldarg.0 callvirt TResult System.Func`2<System.Double,System.Double>::Invoke(T) sub ldc.r8 0.000001 div ret For numerical calculation of derivatives, other, more accurate methods can be used .
Testing
Testing was conducted for several processing steps, which can be viewed in the project MathFunction.Tests. Among the interesting points, we can mention the use of WolframAlpha.NET for testing analytical derivatives and loading and unloading assemblies using domains.
Wolframlpha
WolframAlpha.NET is an API wrapper for the famous wolframalpha math service . In my project, it was useful in order to verify the obviously correct derivative obtained on this service with the derivative obtained with the help of my library. Used as follows:
public static bool CheckDerivative(string expression, string derivative) { return CheckEquality("diff(" + expression + ")", derivative); } public static bool CheckEquality(string expression1, string expression2) { WolframAlpha wolfram = new WolframAlpha(ConfigurationManager.AppSettings["WolframAlphaAppId"]); string query = "(" + expression1.Replace(" ", "") + ")-(" + expression2.Replace(" ", "") + ")"; QueryResult result = wolfram.Query(query); result.RecalculateResults(); try { double d; return double.TryParse(result.GetPrimaryPod().SubPods[0].Plaintext, out d) && d == 0.0; } catch { return false; } } Loading and unloading assemblies using domains
Creating a domain, assembling from a file, creating an instance of a certain type and getting objects with information about methods (MethodInfo):
Domain = AppDomain.CreateDomain("MathFuncDomain"); MathFuncObj = _domain.CreateInstanceFromAndUnwrap(FileName, NamespaceName + "." + ClassName); Type mathFuncObjType = _mathFuncObj.GetType(); Func = mathFuncObjType.GetMethod(FuncName); FuncDerivative = mathFuncObjType.GetMethod(FuncDerivativeName); Calculation of the result of the compiled function:
return (double)Func.Invoke(_mathFuncObj, new object[] { x }) Uploading a domain and deleting a file with an assembly:
if (_domain != null) AppDomain.Unload(Domain); File.Delete(FileName); Comparison of generated IL code
The final IL code is more optimal, compared to the code generated by the standard C # compiler csc.exe in Release mode, you just have to look at the comparison of the following two listings, for example, for the function
x ^ 3 + sin(3 * ln(x * 1)) + x ^ ln(2 * sin(3 * ln(x))) - 2 * x ^ 3 | csc.exe .NET 4.5.1 | MathExpressions.NET |
| |
It is curious to see at the same time what kind of disassembled C # code in ILSpy is for a function which is a derivative of the above function, i.e. to
(ln(2 * sin(3 * ln(x))) * x ^ -1 + 3 * ln(x) * cos(3 * ln(x)) * sin(3 * ln(x)) ^ -1 * x ^ -1) * x ^ ln(2 * sin(3 * ln(x))) + 3 * cos(3 * ln(x)) * x ^ -1 + -(3 * x ^ 2) double arg_24_0 = 2.0; double arg_1A_0 = 3.0; double num = Math.Log(x); double num2 = arg_1A_0 * num; double num3 = Math.Sin(num2); double num4 = Math.Log(arg_24_0 * num3); double arg_3B_0 = num4; double num5 = 1.0 / x; double arg_54_0 = arg_3B_0 * num5; double arg_4F_0 = 3.0 * num; num = Math.Cos(num2); return (arg_54_0 + arg_4F_0 * num / num3 * num5) * Math.Pow(x, num4) + num * num5 * 3.0 - x * x * 3.0; As you can see, a large number of local variables have been created to store the already calculated results of functions. Although in reality there are fewer local variables, because, for example, for double arg_24_0 = 2.0; no local variable is created, it is just a constant.
Of course, in real-world applications, such expressions are rarely encountered, but, nevertheless, the described optimizations can be used in other, more practical cases and for a better understanding of the compiler's work.
Conclusion
During the implementation of all of the above in C #, I realized that a functional language is more suitable for tasks where you need to do something related to symbolic computation and substitution. Even, for example, the OpenSource maxima computer algebra system is written in lisp. By the way, on F # there is an implementation of symbolic calculations on the codeproject , and there is clearly less code than I have in the project. However, the implementation of this project allowed me to gain more experience in parsing expressions, optimizing, generating low-level code, working with floating point numbers and just in mathematics.
For all interested, I posted it on Github: source . The program itself is also available: MathExpressions.NET. If absolutely necessary, I can refactor it. Pull requests are welcome.
PS A long formula is hidden in the heart, taking into account the permutation of the terms, the factors and the simplification. During its complication the developed program was used.
UPDATE: Since no one has guessed what is encrypted in the heart, I post the result. This formula is a special case of a Matiyasevich polynomial whose set of positive values for non-negative values of variables coincides with the set of primes. Wikipedia also has information .
Source: https://habr.com/ru/post/150043/
All Articles