Optimization of the algorithm for checking the Delaunay condition through the equation of the circumscribed circle and its application
I'll tell you a secret about how quickly to check the fulfillment of the Delone condition for two triangles.
Actually, the optimization itself is described a little lower (see “Optimization of the algorithm for checking the Delaunay condition through the equation of the circumcircle”), but I will tell everything in order.
In my case, triangulation is used in image tracing, to split a plane into primitive sectors (triangles). As you know, it is also divided into several stages: adjustment, identification of boundaries, detouring of borders, sweeping of contours. This is in its most general form. I would like to stop, I think, at the most difficult stage: sweeping up the plane.
After detecting and traversing the boundaries at the exit, I got a lot of external contours. Each contacting contours have different colors. Inside each such circuit there is also a known number of internal circuits.
Thus, from the point of view of “sweeping up the plane,” if we consider the outer contours separately, we have a set of points, each of which has one neighbor on the right and left. Those. all points are closed in a chain, there is not a single “hanging” point, and there are at least 3 points in each chain (Figure 1).
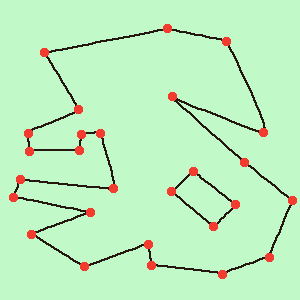
Picture 1
')
It is necessary to sweep the shape of triangles.
After reading the book [1], I did not find a single (at least one) method of constructing the Delaunay triangulation at least in any way suitable to my case. Search for other books did not. Yes, and this was enough, she brought the thoughts of my head in order. As a result, invented his "bicycle".
1) Suppose, to begin with, that in the figure under consideration there is only one sequence. Then it all comes down to the consistent picking up of triangles. Take any point and try to build a triangle with adjacent points. If the triangle cannot be built (the line connecting these two points intersects with the already constructed ones or the line passes in the exclusion zone (Figure 2), move to the next point, let's say to the right. When the next triangle is found, put it in the list (Figure 3), the point from which it was built is deleted (Figure 4).

Figure 2
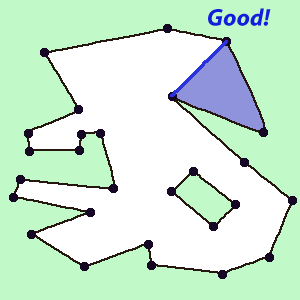
Figure 3

Figure 4
One more thing: when saving the next triangle, it is necessary to record vertices in a roundabout in a clockwise direction (in the right coordinate system). This is useful later to reduce computational resources.
2) Repeat step 1 until we sweep the entire plane.
3) If there are several sequences, i.e. one, and inside it one more or more internal contours (Figure 1). Here it is necessary to consider each sequence separately. Take the next inner contour. From one external and one internal we will make two single contours. To do this, you need to find two "ports" from one circuit to another. The condition for “ports”: they should not intersect each other (they should not even touch the ends), they should not intersect with the contour lines (Figure 5).

Figure 5
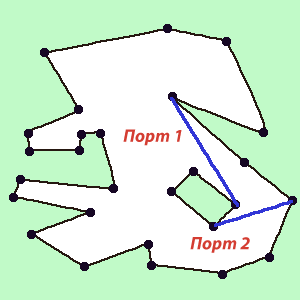
Figure 6
4) Next, you should enter in turn all the internal sequences into already formed, separated from each other (paragraph 3) sequences. You need to merge with the one that contains the new one. By definition, no internal sequence touches or intersects with others (both external and all possible internal), so that everything goes smoothly.
Having found the ports (Figure 6) it is easy to build new sequences and bypass them in points 1 and 2 of the current algorithm (Figure 7).
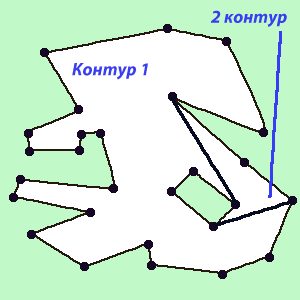
Figure 7
5) After the 4th stage, we have a list of triangles (Figure 8). As if the task had already been done, it remains to make the picture beautiful: check that the Delone condition is met (Figure 9).
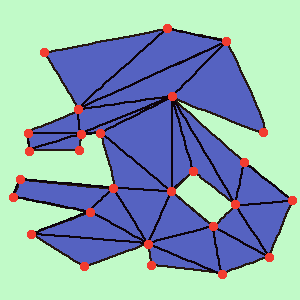
Figure 8
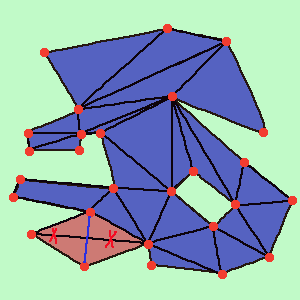
Figure 9
6) Looking ahead, I will tell you about the sixth paragraph. It consists in a sequential run through the list of triangles obtained by item No. 5. First we mark all triangles as “dirty”. In each cycle, we check for each triangle Delone condition. If the condition is not met, then we do the rebuilding and mark the neighbors and the current triangle as “dirty”. If the condition is satisfied, then mark it clean. In my implementation of the algorithm, each triangle has a link to its neighbors. In this case, the 6th item is the fastest.
Now, as far as I know, there are two possible ways to determine whether the triangles satisfy the Delone condition or not: 1) Check the sum of opposite corners. It should be less than 180. 2) Calculate the center of the circumscribed circle and calculate the distance to the 4th point. Everyone knows the Delone condition is satisfied if the point is outside the circumscribed circle.
Computational power number 1: 10 multiplication / division operations and 13 addition / subtraction operations.
Computational power number 2: 29 multiplication / division operations and 24 addition / subtraction operations.
From the point of view of computing power, which is calculated for example in the book [1], option No. 1 is more advantageous. I realized it if it were not for ... (Figure 10). As it turned out after putting this method on the “conveyor”, there was an uncertainty. This is an option when the angle A itself is more than 180 degrees. It is considered in the book [1] as one of the individual particular methods. And with it all its elegance, transparency and performance disappears. As well, it later turned out that method No. 2 can be very significantly optimized.
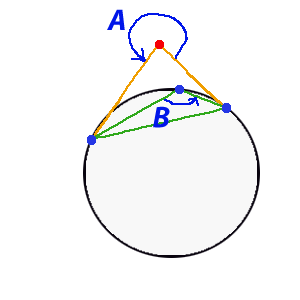
Figure 10
Further pure mathematics.
So we have:
Checking the condition for the point M (X, Y) by the equation of a circle passing through the points A (x1, y1), B (x2, y2), C (x3, y3) can be written in the form:
(a ⋅ (X ^ 2 + Y ^ 2) - b ⋅ X + c Y - d) ⋅ sign a ≥ 0
Details can be found in the magnificent book [1]. (No, I'm not its author)
So, sign a is a sign of the direction of the walk, from the very beginning I built triangles clockwise, so it can be omitted (it is equal to one).
Next, moving the center of coordinates to the point M, we get (Figure 11):
A (x1 - X, y1 - Y), B (x2 - X, y2 - Y), B (x3 - X, y3 - Y);
-d> = 0
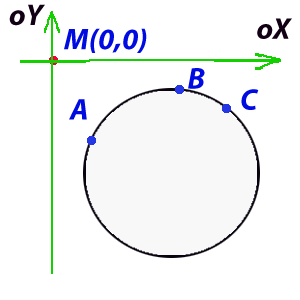
Figure 11
Just isn't it?
d <= 0
According to the book, again, [1]
We have: 15 multiplication / division operations and 14 addition / subtraction operations.
Thanks for attention. Waiting for critics.
1. Skvortsov A.V. Delaunay triangulation and its application. - Tomsk: Publishing house Tom. University, 2002. - 128 p. ISBN 5-7511-1501-5
Actually, the optimization itself is described a little lower (see “Optimization of the algorithm for checking the Delaunay condition through the equation of the circumcircle”), but I will tell everything in order.
In my case, triangulation is used in image tracing, to split a plane into primitive sectors (triangles). As you know, it is also divided into several stages: adjustment, identification of boundaries, detouring of borders, sweeping of contours. This is in its most general form. I would like to stop, I think, at the most difficult stage: sweeping up the plane.
At the entrance
After detecting and traversing the boundaries at the exit, I got a lot of external contours. Each contacting contours have different colors. Inside each such circuit there is also a known number of internal circuits.
Thus, from the point of view of “sweeping up the plane,” if we consider the outer contours separately, we have a set of points, each of which has one neighbor on the right and left. Those. all points are closed in a chain, there is not a single “hanging” point, and there are at least 3 points in each chain (Figure 1).

Picture 1
')
What need to do
It is necessary to sweep the shape of triangles.
Search
After reading the book [1], I did not find a single (at least one) method of constructing the Delaunay triangulation at least in any way suitable to my case. Search for other books did not. Yes, and this was enough, she brought the thoughts of my head in order. As a result, invented his "bicycle".
Algorithm
1) Suppose, to begin with, that in the figure under consideration there is only one sequence. Then it all comes down to the consistent picking up of triangles. Take any point and try to build a triangle with adjacent points. If the triangle cannot be built (the line connecting these two points intersects with the already constructed ones or the line passes in the exclusion zone (Figure 2), move to the next point, let's say to the right. When the next triangle is found, put it in the list (Figure 3), the point from which it was built is deleted (Figure 4).

Figure 2

Figure 3

Figure 4
One more thing: when saving the next triangle, it is necessary to record vertices in a roundabout in a clockwise direction (in the right coordinate system). This is useful later to reduce computational resources.
2) Repeat step 1 until we sweep the entire plane.
3) If there are several sequences, i.e. one, and inside it one more or more internal contours (Figure 1). Here it is necessary to consider each sequence separately. Take the next inner contour. From one external and one internal we will make two single contours. To do this, you need to find two "ports" from one circuit to another. The condition for “ports”: they should not intersect each other (they should not even touch the ends), they should not intersect with the contour lines (Figure 5).

Figure 5

Figure 6
4) Next, you should enter in turn all the internal sequences into already formed, separated from each other (paragraph 3) sequences. You need to merge with the one that contains the new one. By definition, no internal sequence touches or intersects with others (both external and all possible internal), so that everything goes smoothly.
Having found the ports (Figure 6) it is easy to build new sequences and bypass them in points 1 and 2 of the current algorithm (Figure 7).

Figure 7
5) After the 4th stage, we have a list of triangles (Figure 8). As if the task had already been done, it remains to make the picture beautiful: check that the Delone condition is met (Figure 9).

Figure 8

Figure 9
6) Looking ahead, I will tell you about the sixth paragraph. It consists in a sequential run through the list of triangles obtained by item No. 5. First we mark all triangles as “dirty”. In each cycle, we check for each triangle Delone condition. If the condition is not met, then we do the rebuilding and mark the neighbors and the current triangle as “dirty”. If the condition is satisfied, then mark it clean. In my implementation of the algorithm, each triangle has a link to its neighbors. In this case, the 6th item is the fastest.
More on the fifth stage
Now, as far as I know, there are two possible ways to determine whether the triangles satisfy the Delone condition or not: 1) Check the sum of opposite corners. It should be less than 180. 2) Calculate the center of the circumscribed circle and calculate the distance to the 4th point. Everyone knows the Delone condition is satisfied if the point is outside the circumscribed circle.
Computational power number 1: 10 multiplication / division operations and 13 addition / subtraction operations.
Computational power number 2: 29 multiplication / division operations and 24 addition / subtraction operations.
From the point of view of computing power, which is calculated for example in the book [1], option No. 1 is more advantageous. I realized it if it were not for ... (Figure 10). As it turned out after putting this method on the “conveyor”, there was an uncertainty. This is an option when the angle A itself is more than 180 degrees. It is considered in the book [1] as one of the individual particular methods. And with it all its elegance, transparency and performance disappears. As well, it later turned out that method No. 2 can be very significantly optimized.

Figure 10
Optimization of the algorithm for checking the Delaunay condition through the equation of the circumscribed circle
Further pure mathematics.
So we have:
Checking the condition for the point M (X, Y) by the equation of a circle passing through the points A (x1, y1), B (x2, y2), C (x3, y3) can be written in the form:
(a ⋅ (X ^ 2 + Y ^ 2) - b ⋅ X + c Y - d) ⋅ sign a ≥ 0
Details can be found in the magnificent book [1]. (No, I'm not its author)
So, sign a is a sign of the direction of the walk, from the very beginning I built triangles clockwise, so it can be omitted (it is equal to one).
Next, moving the center of coordinates to the point M, we get (Figure 11):
A (x1 - X, y1 - Y), B (x2 - X, y2 - Y), B (x3 - X, y3 - Y);
-d> = 0

Figure 11
Just isn't it?
d <= 0
According to the book, again, [1]
(x1^2 + y1^2)*(y2*x3 - x2*y3) + (x2^2 + y2^2)*(x1*y3 - y1*x3) + (x3^2 + y3^2)*(y1*x2 - x1*y2) <= 0 We have: 15 multiplication / division operations and 14 addition / subtraction operations.
Thanks for attention. Waiting for critics.
Bibliography
1. Skvortsov A.V. Delaunay triangulation and its application. - Tomsk: Publishing house Tom. University, 2002. - 128 p. ISBN 5-7511-1501-5
Source: https://habr.com/ru/post/149911/
All Articles