Random search heuristics and motor ships
Once upon a time I had already written a fairly large article on the use of heuristics in programming , but today I want to give a small practical example. This summer, I sailed on the Moscow-Rostov-on-Don-Moscow route, and noticed that every evening the cruise director was trying to find the optimal seating group for tourist groups on buses. The task is not so difficult, but at least 15 minutes a day is spent on its solution. Of course, I tried to automate this process.
But, before describing my solution, it is necessary to formulate the problem more precisely. At the very beginning of the cruise, all the tourists were divided into several excursion groups (in the case under consideration there were 15 groups), with no more than 10 people in each group. All groups were numbered in order, and the resulting list of groups did not change until the very end of the cruise. This list looked like this:
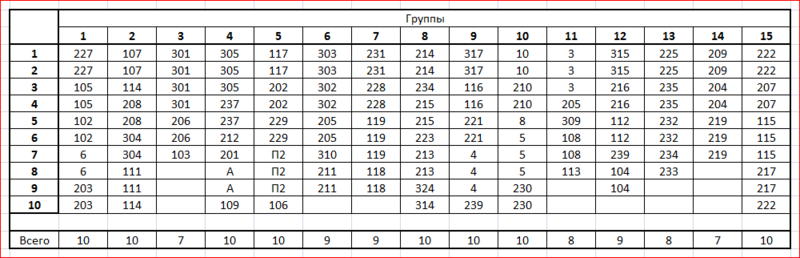Every day, tourists notify the director of the cruise about what excursions they are planning to go. Anyone who does not plan to go on the main tour, cross out of this list. It is with the modified list that we have to work. The director of the cruise counts how many people go on a tour (usually 100-120 people) and makes an appropriate order for buses. Travel agencies on the coast take this order and report the following information: “Three buses with 48, 48 and 50 seats will be waiting for you at the pier”. As a result, the task turns out to be the following: it is necessary to seat the tourists in buses, observing the following requirements (in order of importance):
1. Do not split the group;
2. Fill buses as evenly as possible;
3. It is desirable that groups sitting in the same bus go in a row. Those. the first bus is groups 1-5, the second bus is 6-10, etc.
The first step towards automation was made using Excel and the “Search for Solution” add-on (to my surprise, very few people know about this setting, although the piece is incredibly useful).
The first requirement, of course, was fulfilled, but the second and third requirements had to be forgotten. Considering that the search for a solution took about 15 seconds on an old laptop, it was decided to write my bike. But here again there was a question how to do all this: the simplex method, dynamic programming, the branch and bound method, heuristics? Surely there is some complicated algorithm that will help in solving this problem, but writing something complicated on vacation, and then debugging it on a laptop with a small screen? I decided to try some heuristics. I immediately put off climbing the hill after some hesitation, as well as the heuristics of the minimum cost and balanced profit.
And then I remembered the random search heuristics. To be honest, I have never used it before, and I was almost sure that a random search would not lead to an effective solution. But curiosity took over. The result is the following algorithm of seating:
1. Choose a random group and a random bus.
2. Check whether we can put the selected group in the selected bus (we look, if this group is not sitting in another bus, and if there are enough seats)
2.1. If we cannot, then we increase the counter of unsuccessful attempts by one.
2.2. If we can, reset the failed attempts counter.
3. If the number of unsuccessful attempts exceeded 50, we exit the cycle, otherwise, to item 1
4. Check if all groups are seated.
4.1. If all, calculate the maximum difference between the number of empty seats in buses (this is the number that will be considered an estimate)
4.2. If not all, report an unsuccessful seating.
Performing this procedure hundreds of times, we can choose a seating with the best estimate. This algorithm worked surprisingly well. At least the first and second points of the requirements were met perfectly.
To execute the third point, a small change is needed in the algorithm. Even before the start of the implementation of the seating algorithm, we will plant in each bus 5 groups (1-5.6-10.11-15-15), and perform the seating. If she succeeds, we remember the best estimate, and the result is output. Then we try to put 4 groups in each bus (1-4, 5-8, ...), and again we carry out the seating. If the estimate obtained turned out to be better than it was at the previous stage, we memorize it and again display the result. Then we try to put the bus into groups of 2, 2, and 1 groups each, and finally, we perform the seating procedure without any prior information. If at some stage, the estimate has improved, the resulting solution is displayed.
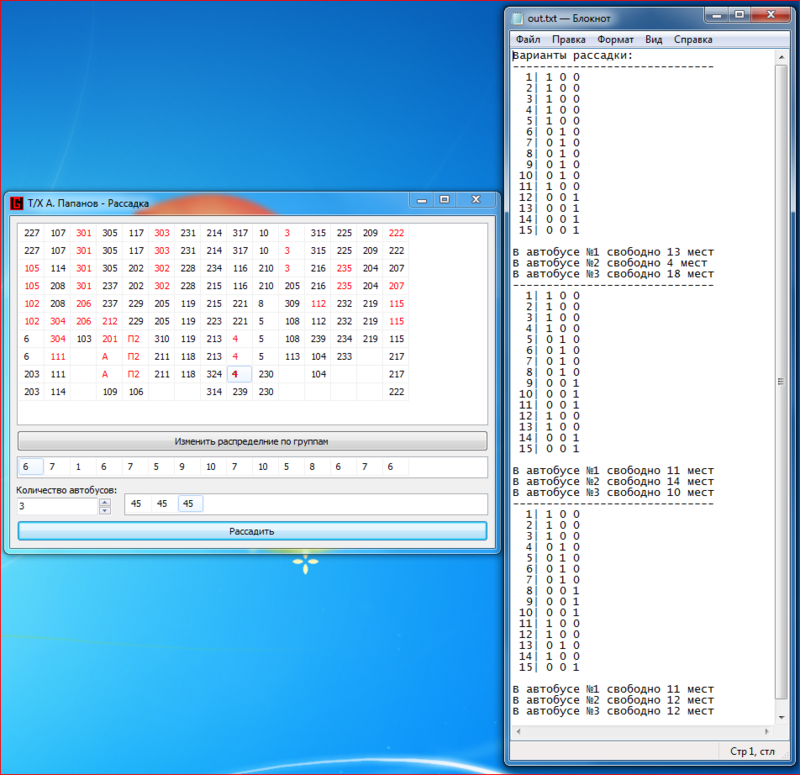
Of course, more actions are performed, but the value of the results obtained is much higher. Lastly, I will give a small example of the program:
It is clear that most of you already know about random search heuristics, but suddenly this post was read by people who do not know about it, or for some reason were afraid to use it. I hope that now, having learned this heuristic a little better, you can at least simplify a little the solution of some of your problems.
But, before describing my solution, it is necessary to formulate the problem more precisely. At the very beginning of the cruise, all the tourists were divided into several excursion groups (in the case under consideration there were 15 groups), with no more than 10 people in each group. All groups were numbered in order, and the resulting list of groups did not change until the very end of the cruise. This list looked like this:
Every day, tourists notify the director of the cruise about what excursions they are planning to go. Anyone who does not plan to go on the main tour, cross out of this list. It is with the modified list that we have to work. The director of the cruise counts how many people go on a tour (usually 100-120 people) and makes an appropriate order for buses. Travel agencies on the coast take this order and report the following information: “Three buses with 48, 48 and 50 seats will be waiting for you at the pier”. As a result, the task turns out to be the following: it is necessary to seat the tourists in buses, observing the following requirements (in order of importance):1. Do not split the group;
2. Fill buses as evenly as possible;
3. It is desirable that groups sitting in the same bus go in a row. Those. the first bus is groups 1-5, the second bus is 6-10, etc.
The first step towards automation was made using Excel and the “Search for Solution” add-on (to my surprise, very few people know about this setting, although the piece is incredibly useful).
The first requirement, of course, was fulfilled, but the second and third requirements had to be forgotten. Considering that the search for a solution took about 15 seconds on an old laptop, it was decided to write my bike. But here again there was a question how to do all this: the simplex method, dynamic programming, the branch and bound method, heuristics? Surely there is some complicated algorithm that will help in solving this problem, but writing something complicated on vacation, and then debugging it on a laptop with a small screen? I decided to try some heuristics. I immediately put off climbing the hill after some hesitation, as well as the heuristics of the minimum cost and balanced profit.And then I remembered the random search heuristics. To be honest, I have never used it before, and I was almost sure that a random search would not lead to an effective solution. But curiosity took over. The result is the following algorithm of seating:
1. Choose a random group and a random bus.
2. Check whether we can put the selected group in the selected bus (we look, if this group is not sitting in another bus, and if there are enough seats)
2.1. If we cannot, then we increase the counter of unsuccessful attempts by one.
2.2. If we can, reset the failed attempts counter.
3. If the number of unsuccessful attempts exceeded 50, we exit the cycle, otherwise, to item 1
4. Check if all groups are seated.
4.1. If all, calculate the maximum difference between the number of empty seats in buses (this is the number that will be considered an estimate)
4.2. If not all, report an unsuccessful seating.
Performing this procedure hundreds of times, we can choose a seating with the best estimate. This algorithm worked surprisingly well. At least the first and second points of the requirements were met perfectly.
To execute the third point, a small change is needed in the algorithm. Even before the start of the implementation of the seating algorithm, we will plant in each bus 5 groups (1-5.6-10.11-15-15), and perform the seating. If she succeeds, we remember the best estimate, and the result is output. Then we try to put 4 groups in each bus (1-4, 5-8, ...), and again we carry out the seating. If the estimate obtained turned out to be better than it was at the previous stage, we memorize it and again display the result. Then we try to put the bus into groups of 2, 2, and 1 groups each, and finally, we perform the seating procedure without any prior information. If at some stage, the estimate has improved, the resulting solution is displayed.
Of course, more actions are performed, but the value of the results obtained is much higher. Lastly, I will give a small example of the program:
It is clear that most of you already know about random search heuristics, but suddenly this post was read by people who do not know about it, or for some reason were afraid to use it. I hope that now, having learned this heuristic a little better, you can at least simplify a little the solution of some of your problems.
')
Source: https://habr.com/ru/post/149821/
All Articles