KNN classifier
kNN stands for k Nearest Neighbor or k Nearest Neighbors - this is one of the simplest classification algorithms, also sometimes used in regression problems. Because of its simplicity, it is a good example from which to start exploring the field of machine learning. This article describes an example of writing the code of such a classifier in python, as well as visualization of the results.
The task of classification in machine learning is the task of assigning an object to one of the predefined classes on the basis of its formalized features. Each of the objects in this problem is represented as a vector in N-dimensional space, each dimension in which is a description of one of the features of the object. Suppose we need to classify monitors: dimensions in our parameter space will be the diagonal size in inches, aspect ratio, maximum resolution, HDMI interface, cost, etc. The case of text classification is somewhat more complicated, they usually use a term-document matrix ( described in machinelearning .ru ).
To train a classifier, you must have a set of objects for which classes are predefined. This set is called a training set, its marking is done manually, with the involvement of specialists in the field of study. For example, in the Detecting Insults in Social Commentary problem for pre-assembled tests of comments by a person, the opinion is put on whether this comment is an insult to one of the participants in the discussion, the task itself is an example of a binary classification. In the classification problem there can be more than two classes (multi-class), each of the objects can belong to more than one class (intersecting).
To classify each of the test sample objects, you must perform the following operations sequentially:
The examples below are implemented in python. For their correct execution, besides python, you must have numpy , pylab and matplotlib installed . The library initialization code is as follows:
')
Consider the work of the classifier by example. To begin with, we need to generate data on which experiments will be performed:
For simplicity, I chose a two-dimensional space in which the location of the expectation of a two-dimensional Gaussian with a standard deviation of 0.5 is chosen randomly from 0 to 5 along each axis. A value of 0.5 is chosen so that the objects are well separable enough ( three sigma rule ).
To look at the received sample, you need to run the following code:
Here is an example of the image resulting from the execution of this code:
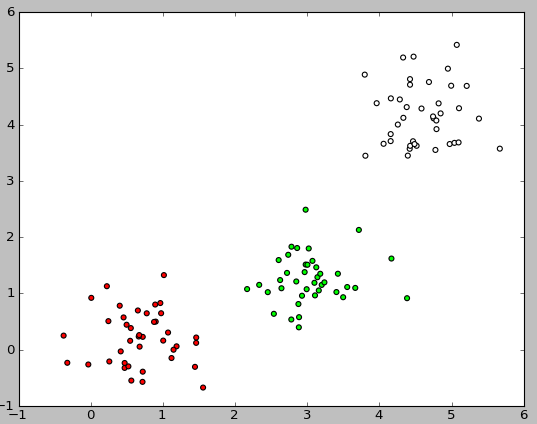
So, we have a set of objects, for each of which a class is defined. Now we need to break this set into two parts: a training choice and a test sample. To do this, use the following code:
Now, having a training sample, it is possible to implement the classification algorithm itself:
To determine the distance between objects, you can use not only the Euclidean distance: the Manhattan distance, the cosine measure, the Pearson correlation criterion, etc. are also used.
Now you can evaluate how well our classifier works. To do this, we will generate data, divide it into a training and test sample, classify the objects of the test sample and compare the real value of the class with the resulting classification:
To assess the quality of the classifier's work, various algorithms and various measures are used, you can read in more detail here: wiki
Now the most interesting thing remains: to show the classifier's work graphically. In the pictures below, I used 3 classes, each with 40 elements, the value of k for the algorithm was equal to three.


The following code is used to display these pictures:
kNN is one of the simplest classification algorithms, so it often turns out to be ineffective in real-world problems. In addition to classification accuracy, the problem of this classifier is the classification speed: if there are N objects in the training sample, M objects in the test choice, and K is the dimension of space, then the number of operations for classifying a test sample can be O (K * M * N). Nevertheless, the kNN workflow is a good example to start exploring Machine Learning.
1. The method of nearest neighbors on Machinelearning.ru
2. Vector model on Machinelearning.ru
3. Book on Information Retrieval
4. Description of the method of the nearest neighbors in the framework of scikit-learn
5. The book "Programming the collective mind"
The task of classification in machine learning is the task of assigning an object to one of the predefined classes on the basis of its formalized features. Each of the objects in this problem is represented as a vector in N-dimensional space, each dimension in which is a description of one of the features of the object. Suppose we need to classify monitors: dimensions in our parameter space will be the diagonal size in inches, aspect ratio, maximum resolution, HDMI interface, cost, etc. The case of text classification is somewhat more complicated, they usually use a term-document matrix ( described in machinelearning .ru ).
To train a classifier, you must have a set of objects for which classes are predefined. This set is called a training set, its marking is done manually, with the involvement of specialists in the field of study. For example, in the Detecting Insults in Social Commentary problem for pre-assembled tests of comments by a person, the opinion is put on whether this comment is an insult to one of the participants in the discussion, the task itself is an example of a binary classification. In the classification problem there can be more than two classes (multi-class), each of the objects can belong to more than one class (intersecting).
Algorithm
To classify each of the test sample objects, you must perform the following operations sequentially:
- Calculate the distance to each of the objects of the training sample
- Select k objects of the training sample, the distance to which is minimal
- The class of the object being classified is the class most often found among the k nearest neighbors.
The examples below are implemented in python. For their correct execution, besides python, you must have numpy , pylab and matplotlib installed . The library initialization code is as follows:
import random import math import pylab as pl import numpy as np from matplotlib.colors import ListedColormap ')
Initial data
Consider the work of the classifier by example. To begin with, we need to generate data on which experiments will be performed:
#Train data generator def generateData (numberOfClassEl, numberOfClasses): data = [] for classNum in range(numberOfClasses): #Choose random center of 2-dimensional gaussian centerX, centerY = random.random()*5.0, random.random()*5.0 #Choose numberOfClassEl random nodes with RMS=0.5 for rowNum in range(numberOfClassEl): data.append([ [random.gauss(centerX,0.5), random.gauss(centerY,0.5)], classNum]) return data For simplicity, I chose a two-dimensional space in which the location of the expectation of a two-dimensional Gaussian with a standard deviation of 0.5 is chosen randomly from 0 to 5 along each axis. A value of 0.5 is chosen so that the objects are well separable enough ( three sigma rule ).
To look at the received sample, you need to run the following code:
def showData (nClasses, nItemsInClass): trainData = generateData (nItemsInClass, nClasses) classColormap = ListedColormap(['#FF0000', '#00FF00', '#FFFFFF']) pl.scatter([trainData[i][0][0] for i in range(len(trainData))], [trainData[i][0][1] for i in range(len(trainData))], c=[trainData[i][1] for i in range(len(trainData))], cmap=classColormap) pl.show() showData (3, 40) Here is an example of the image resulting from the execution of this code:

Getting a training and test sample
So, we have a set of objects, for each of which a class is defined. Now we need to break this set into two parts: a training choice and a test sample. To do this, use the following code:
#Separate N data elements in two parts: # test data with N*testPercent elements # train_data with N*(1.0 - testPercent) elements def splitTrainTest (data, testPercent): trainData = [] testData = [] for row in data: if random.random() < testPercent: testData.append(row) else: trainData.append(row) return trainData, testData Implementation of the classifier
Now, having a training sample, it is possible to implement the classification algorithm itself:
#Main classification procedure def classifyKNN (trainData, testData, k, numberOfClasses): #Euclidean distance between 2-dimensional point def dist (a, b): return math.sqrt((a[0] - b[0])**2 + (a[1] - b[1])**2) testLabels = [] for testPoint in testData: #Claculate distances between test point and all of the train points testDist = [ [dist(testPoint, trainData[i][0]), trainData[i][1]] for i in range(len(trainData))] #How many points of each class among nearest K stat = [0 for i in range(numberOfClasses)] for d in sorted(testDist)[0:k]: stat[d[1]] += 1 #Assign a class with the most number of occurences among K nearest neighbours testLabels.append( sorted(zip(stat, range(numberOfClasses)), reverse=True)[0][1] ) return testLabels To determine the distance between objects, you can use not only the Euclidean distance: the Manhattan distance, the cosine measure, the Pearson correlation criterion, etc. are also used.
Execution examples
Now you can evaluate how well our classifier works. To do this, we will generate data, divide it into a training and test sample, classify the objects of the test sample and compare the real value of the class with the resulting classification:
#Calculate classification accuracy def calculateAccuracy (nClasses, nItemsInClass, k, testPercent): data = generateData (nItemsInClass, nClasses) trainData, testDataWithLabels = splitTrainTest (data, testPercent) testData = [testDataWithLabels[i][0] for i in range(len(testDataWithLabels))] testDataLabels = classifyKNN (trainData, testData, k, nClasses) print "Accuracy: ", sum([int(testDataLabels[i]==testDataWithLabels[i][1]) for i in range(len(testDataWithLabels))]) / float(len(testDataWithLabels)) To assess the quality of the classifier's work, various algorithms and various measures are used, you can read in more detail here: wiki
Now the most interesting thing remains: to show the classifier's work graphically. In the pictures below, I used 3 classes, each with 40 elements, the value of k for the algorithm was equal to three.


The following code is used to display these pictures:
#Visualize classification regions def showDataOnMesh (nClasses, nItemsInClass, k): #Generate a mesh of nodes that covers all train cases def generateTestMesh (trainData): x_min = min( [trainData[i][0][0] for i in range(len(trainData))] ) - 1.0 x_max = max( [trainData[i][0][0] for i in range(len(trainData))] ) + 1.0 y_min = min( [trainData[i][0][1] for i in range(len(trainData))] ) - 1.0 y_max = max( [trainData[i][0][1] for i in range(len(trainData))] ) + 1.0 h = 0.05 testX, testY = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) return [testX, testY] trainData = generateData (nItemsInClass, nClasses) testMesh = generateTestMesh (trainData) testMeshLabels = classifyKNN (trainData, zip(testMesh[0].ravel(), testMesh[1].ravel()), k, nClasses) classColormap = ListedColormap(['#FF0000', '#00FF00', '#FFFFFF']) testColormap = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAAA']) pl.pcolormesh(testMesh[0], testMesh[1], np.asarray(testMeshLabels).reshape(testMesh[0].shape), cmap=testColormap) pl.scatter([trainData[i][0][0] for i in range(len(trainData))], [trainData[i][0][1] for i in range(len(trainData))], c=[trainData[i][1] for i in range(len(trainData))], cmap=classColormap) pl.show() Conclusion
kNN is one of the simplest classification algorithms, so it often turns out to be ineffective in real-world problems. In addition to classification accuracy, the problem of this classifier is the classification speed: if there are N objects in the training sample, M objects in the test choice, and K is the dimension of space, then the number of operations for classifying a test sample can be O (K * M * N). Nevertheless, the kNN workflow is a good example to start exploring Machine Learning.
Bibliography
1. The method of nearest neighbors on Machinelearning.ru
2. Vector model on Machinelearning.ru
3. Book on Information Retrieval
4. Description of the method of the nearest neighbors in the framework of scikit-learn
5. The book "Programming the collective mind"
Source: https://habr.com/ru/post/149693/
All Articles