Zxcvbn program: realistic password strength assessment

For the past few months, password strength analyzers have come across to me in almost every online registration form. In this area today there is a particularly rapid growth.

The only question is, does such a program really help protect a user account? This aspect of Internet security is of course not as important as some others, for example:

• Prevent hacking of web pages due to increasing delay or using CAPTCHA;
• prevention of offline hacking by using a fairly slow hash function with a “salt” individualized at the user level;
• password hashes protection.

If we take into account the above factors, then yes, I am sure that programs testing password security are really very promising and can help the user . In his book, published in 2006, entitled “Perfect Passwords: Choice, Protection, Authentication” (Perfect Passwords: Selection, Protection, Authentication) , Mark Burnett (Mark Burnett), calculated the frequency of several million passwords used as a result of various leaks data. He writes that every ninth user chose a password from this list of the most popular . Among them are such "tough nuts" as: password1, compaq, 7777777, merlin and rosebud. Last year, Burnett conducted a new study , examining 6 million passwords, and this time it turned out that 99.8% of them are on the list of 10,000 most popular, and 91% are on the list of 1000 most common. Of course, the result was largely influenced by the research methodology and sample offset - for example, since most of these passwords were obtained from already cracked hashes, the entire list was initially shifted to easily cracked passwords.

Only easily guessed passwords are listed here, but I bet that a large percentage of the rest are still quite predictable and can be cracked as a result of a small network attack. Therefore, I believe that thanks to direct interaction with users, such analyzers can really help in choosing a more reliable password. However, at the moment they, for the most part, only harm (not counting several programs with closed code). That is why it happens.
Password strength is best measured by the amount of entropy expressed in bits. Entropy is calculated as the number of options for dividing into two possible passwords. Here is the simplest password strength estimation algorithm:

# n:   # c:  :    # (26  ,     , 62 —  ,      ,   )  = n * lg(c) #    2 

')
Such an analysis by the method of direct selection is applicable to passwords consisting of random sequences of letters, numbers and symbols. However, in most cases, and only with rare exceptions (for which special thanks to 1Password / KeePass ), people choose ordered combinations of characters as a password — vocabulary words, simple keyboard sequences, for example qwerty, asdf and zxcvbn, repetitions (aaaaaaa), sequences (for example , abcdef or 654321), as well as combinations of the above elements. If the password contains upper case letters, then the first letter of the password is likely to be that letter. The use of numbers and special characters is also often predictable, in particular through the use of l33t network jargon (number 3 replaces the letter e, 0 - o, @ or 4 - a), year, date, zip code, etc.

As a result, simplified methods for analyzing the reliability of a password prove to be unreliable. Without testing the use of common combinations, the recommendation to use numbers and symbols in the password will slightly complicate hacking, but it will significantly complicate memorization. One of the comics on xkcd describes this situation perfectly:
>

That's why I decided as an independent project for another “Cracker Week” conducted by Dropbox to create an open source password strength analyzer that would eliminate simple combinations and, accordingly, would not prohibit quite complex phrase passwords such as correcthorsebatterystaple (right horse battery). Now this utility is available on dropbox.com/register and is available for use on github. You can experiment yourself with the demo version and evaluate several passwords.

The table below compares zxcvbn with other password strength analyzers. The point of comparison is not to prove the failure of other applications — indeed, each site has its own password policy — but to give you a better idea of ​​the features of zxcvbn.

	qwER43@!	Tr0ub4dour&3	correcthorsebatterystaple
zxcvbn
Dropbox (old)
Citibank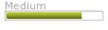
Bank of America	Invalid	Invalid	Invalid
Twitter
Paypal
ebay			Invalid
Facebook
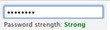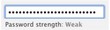Yahoo!
Gmail

A few notes:

• I made these screenshots on April 3, 2012.
• Zxcvbn considers correcthorsebatterystaple to be the most secure password out of three. The remaining applications either consider it the most inefficient, or do not allow it at all. (Twitter assigned the same degree of reliability to the three passwords, but if you look closely, you will notice a slight difference.)
• Zxcvbn considers qwER43 @! inefficient password because it is an encrypted QWERTY keyboard sequence. For each change of direction and shift of the symbol, he increases her entropy.
• Password Analyzer PayPal counted qwER43 @! ineffective password, but aaAA11 !!! - reliable. It can be assumed that he recognizes keyboard sequences.
• The Bank of America registration form does not allow the use of passwords longer than 20 characters, including correcthorsebatterystaple. According to their rules, some special characters can be used in passwords, but “&” and “!” Are not allowed, respectively, the use of the two remaining passwords is prohibited. eBay also does not allow passwords longer than 20 characters.
• It seems that with rare exceptions, the tested programs are not guided by the same primitive criteria as I, otherwise correcthorsebatterystaple would receive the highest rating due to its length. The previous version of Dropbox Password Analyzer added password points for each lower case letter, capital letter, number and special character used up to a certain limit for each of these groups of characters. This approach only protects against brute-force attacks, although this system has the option of checking a new password against the dictionary of the most commonly used words. I don’t know the principles of the rest of the tested programs, but it is known that developers often use such tables of reliability criteria (which, however, check the password using a small set of combinations).
• For the base word of the password in the second column I took Troubadour, not Troubador, as in xkcd (the last spelling is rare).

Installation

The zxcvbn system is not limited to the type of browser and works with Internet Explorer (since version 7) / Opera / FireFox / Safari / Google Chrome. The easiest way to add it to your registration page is the following:

 <script src="zxcvbn-async.js" type="text/javascript"> </script> 

The size of the zxcvbn-async.js script is only 350 bytes. After executing window.load, when the page loads and displays, the download of zxcvbn.js will begin - a “heavy” file of 680 KB (or 320 KB in gzip), most of which is in the dictionary. I have never seen that the size of the script created any problems: since before choosing a password the user usually enters other data on the registration form, there is plenty of time to load the script. Here is a complete description of the asynchronous script download in different browsers.
Zxcvbn adds one function to the global namespace:

 zxcvbn(password, user_inputs) 

It takes one required argument (password) and returns a result object with the following properties:

 result.entropy #  result.crack_time #     (.) result.crack_time_display #    ,    : # «», «6 », «»  . . result.score #  ,  0, 1, 2, 3  4, #     10**2, 10**4, 10**6, # 10**8  , . # (        ) result.match_sequence #   ,   #   result.calculation_time #    ();     

The optional user_inputs argument is an array of strings that zxcvbn will add to its built-in dictionary. Theoretically, it can include any lines, but it is assumed that this will be data entered by the user in other fields of the form (for example, name or email address). Thus, the reliability of the password containing the user's personal data can be rated very low. This list is also convenient for taking into account a special dictionary of a specific site (for example, in my program the specific dictionary of the Dropbox site is taken into account).

The zxcvbn program is written in CoffeeScript. The zxcvbn.js and zxcvbn-async.js files are processed by a closure converter , but if you want to improve the zxcvbn, send me a pull request, the README file contains information about setting up the development environment.
Hereinafter, I describe in detail the principle of operation of zxcvbn.

Model

Zxcvbn works in three stages: match (reconciliation), score (calculation), search (search).

• The match function performs a reconciliation of all known combinations (including intersecting ones). Currently, zxcvbn supports matching with several dictionaries (a dictionary of English words, first and last names, as well as a list of 10,000 most common Burnett passwords), sequential keyboard combinations (QWERTY, Dvorak and digital), repetitions (aaa), numeric and character sequences ( 123, gfedcba), for years in the range from 1900 to 2019, as well as dates (in formats 3-13-1997, 13.3.1997, 1331997). All dictionaries recognize upper case and common equivalents of l33t.
• The score function calculates the degree of entropy for each matched combination separately from the rest of the password (assuming that the burglar knows this combination). A simple example is rrrrr. In this case, the hacker needs to go through all the options for repeating from 1 to 5, starting with a lowercase letter:

 entropy = lg(26*5) #  7  

• The search function uses the principle of "Occam's razor"; from the full set of possibly intersecting coincidences, the search yields the simplest non-intersecting sequence (with minimal entropy). For example, if the password is damnation, it can be broken into 2 words: dam and nation, or be treated as one. In this case, it is important to treat the word exactly as a single whole, because the hacker will select the password as a single word that goes through the words much faster than two. By the way, overlapping combinations are also the main cause of the emergence of such unintentionally fatal domain names as childrens-laughter.com, but without a hyphen (note: children's laughter - children's laughter, children slaughter - infanticide).

The search function is the cornerstone of the model. I'll start with her and go back to the beginning.

Entropy Minimum Search

Zxcvbn calculates the degree of entropy of a password as the sum of the entropies of its constituent parts. Any parts of the password between identified combinations are considered as brute force guesses that also have their own entropy. Here is an example of entropy, consisting of the entropy of the last name, the entropy of the search and the entropy of the keyboard:

 entropy("stockwell4$eR123698745") == surname_entropy("stockwell") + bruteforce_entropy("4$eR") + keypad_entropy("123698745") 

Here we make a serious assumption that the password entropy is the sum of the entropies of its parts. However, this assumption is very conservative. Disregarding the “entropy of the configuration” —that is, the entropy of the number and location of the password parts — zxcvbn intentionally underestimates the total entropy without attributing any value to the password structure: the program assumes that the password structure is already known to the hacker (for example, -numbers "), and counts only the number of attempts to guess the password elements. Thus, the entropy of passwords with a complex structure is greatly underestimated. Cracking the correcthorsebatterystaple password (word-word-word-word), a cracker using programs such as L0phtCrack or John the Ripper, as a rule, first goes through a lot of simpler structures (word, word-number, word-word) until it reaches word word word word word. However, there are three reasons why this lack of a program does not bother me:

• Developing a good structural entropy model is not easy; I do not have statistics on which structures are most often used by users, so for accuracy it is better to underestimate the password entropy.
• With a complex password structure, the sum of the entropy of its parts often already provides it with an excellent complexity rating. For example, even knowing the structure of the word-word-word-word password correcthorsebatterystaple, a cracker will crack this password for centuries.
• Most people do not use complex structures when creating passwords. And neglecting the structure, as a rule, reduces the total entropy by just a few bits.

Having dealt with this assumption, let's consider the effective dynamic algorithm on CoffeeScript, which allows us to find the minimum non-intersecting sequence of matches. Its operation time is O (n • m) for a password of length n, including m possible matches of character combinations (including overlapping ones).

 # :    ,    #       (match.i)    # (match.j)   ,  minimum_entropy_match_sequence = (password, matches) -> # , 26 –  ,       bruteforce_cardinality = calc_bruteforce_cardinality password up_to_k = [] #    k,  backpointers = [] #      k,  #    (match.j = k). #  ,      for k in [0...password.length] #      : #         #   k-1. up_to_k[k] = (up_to_k[k-1] or 0) + lg bruteforce_cardinality backpointers[k] = null for match in matches when match.j = k [i, j] = [match.i, match.j] # ,     i-1 +   #      j candidate_entropy = (up_to_k[i-1] or 0) + calc_entropy(match) if candidate_entropy < up_to_k[j] up_to_k[j] = candidate_entropy backpointers[j] = match #    ,    match_sequence = [] k = password.length – 1 while k >= 0 match = backpointers[k] if match match_sequence.push match k = match.i – 1 else k -= 1 match_sequence.reverse() #  «»    , #   #       : # 1.j = 2.i – 1    1, # 2. make_bruteforce_match = (i, j) -> pattern: 'bruteforce' i: i j: j token: password[i..j] entropy: lg Math.pow(bruteforce_cardinality, j – i + 1) cardinality: bruteforce_cardinality k = 0 match_sequence_copy = [] for match in match_sequence #     [i, j] = [match.i, match.j] if i – k > 0 match_sequence_copy.push make_bruteforce_match(k, i – 1) k = j + 1 match_sequence_copy.push match if k < password.length #  «»   match_sequence_copy.push make_bruteforce_match(k, password.length – 1) match_sequence = match_sequence_copy #    —    « » min_entropy = up_to_k[password.length - 1] or 0 crack_time = entropy_to_crack_time min_entropy #    password: password entropy: round_to_x_digits min_entropy, 3 match_sequence: match_sequence crack_time: round_to_x_digits crack_time, 3 crack_time_display: display_time crack_time score: crack_time_to_score crack_time 

The backpointers [j] array stores a match with a sequence ending in the password position j or a null value if there is no such match in the sequence. With dynamic programming, it is customary to start building the optimal sequence from the end and move in the opposite direction.
Performance is especially important for this script because it works in the browser during the password entry process. To ensure the work of the program, I started with a simple O (2 ^m ) approach to calculating sums for all possible non-overlapping subsets, and the process was very quickly slowed down with the complexity of the task. Now, a full analysis of most passwords for zxcvbn takes no more than a few milliseconds. By the roughest estimate, in Google Chrome on 2.4 GHz Intel Xeon, the correcthorsebatterystaple password is analyzed on average in about 3 ms. The password coRrecth0rseba ++ ery9 / 23 / 2007staple $ takes about 12 ms on average.

Threat Model: The Ratio Between Entropy and Break Time

The concept of entropy is not too transparent indicator. How to understand if the 28-bit password is strong enough? In other words, how to move from entropy estimation directly to the time of hacking? For this, a threat model is applied. Let's pretend that:

• Passwords are stored in the form of hashes with "salt" and "salt" for each user selected randomly, which makes the attack using the rainbow table impractical;
• the cracker managed to steal all the hashes and all the "salt" and now he picks up the password in offline mode at the highest possible speed;
• at the disposal of the hacker several processors.

Some indicative numbers are:

 #   -,  bcrypt/scrypt/PBKDF2,        #   10 . #      —     ,     #      #   ; #     -   ,    #   — ,   ! SINGLE_GUESS = .010 #  NUM_ATTACKERS = 100 #     SECONDS_PER_GUESS = SINGLE_GUESS / NUM_ATTACKERS entropy_to_crack_time = (entropy) -> .5 * Math.pow(2, entropy) * SECONDS_PER_GUESS 

Here I entered a coefficient of 0.5, since we calculate the average time of hacking, and not the time for searching the entire search space.
Perhaps these calculations are too conservative. Large-scale theft of hashes happens quite rarely, and unless an attack is directed directly at you, the attacker is unlikely to transfer 100 cores to your password alone. Typically, an attacker has to guess online, where he is annoyed by network latency, incremental latency and CAPTCHA.

Entropy calculation

Now consider how zxcvbn calculates the entropy of each combination of characters in a password. The entry point is calc_entropy (). This is a simple choice:

 calc_entropy = (match) -> return match.entropy if match.entropy? entropy_func = switch match.pattern when 'repeat' then repeat_entropy when 'sequence' then sequence_entropy when 'digits' then digits_entropy when 'year' then year_entropy when 'date' then date_entropy when 'spatial' then spatial_entropy when 'dictionary' then dictionary_entropy match.entropy = entropy_func match 

Above, I outlined how the repeat_entropy function works. The full text of the entropy calculation code can be independently reviewed on github, but to give you some idea of ​​it, I will describe two other calculation functions: spatial_entropy (the entropy of keyboard combinations) and dictionary_entropy (dictionary entropy).
Consider the qwertyhnm keyboard shortcut. It starts with the q character, its length is 9 characters, and it has three directions of movement: first movement to the right, then down and to the right, then again down and to the right. Parameterize this combination:

 s #     # 47 —   QWERTY/Dvorak, 15 —    PC  16 — #    Macintosh L #  ; L >= 2 t #   ; t <= L – 1 # ,   3     2   («qaw») d #  «»        ; #   QWERTY/Dvorak    4,6 (  g – 6 , #   –  1) 

Then the total space of possibilities includes all possible keyboard combinations of length L or less, having t or less direction changes:


The function “ binomial coefficient from (i - 1) to (j - 1) ” calculates possible configurations of direction changes for a keyboard combination of length i, which has j direction changes. “-1” is added to both elements, since the first change of direction always occurs on the first letter. For each of the j shifts of directions, there are d possible directions, i.e. there are only dj possibilities for each configuration. The burglar must also go through all the initial characters, hence the coefficient s in the formula. The formula itself is very approximate - in particular, because many of the options considered in it are impossible on a real keyboard: for a keyboard combination of length 5 with 1 direction change, the operation “start with“ q ”and move to the left” is taken into account, but impossible.

This CoffeeScript expression can be written like this:

 lg = (n) -> Math.log(n) / Math.log(2) nPk = (n, k) -> return 0 if k > n result = 1 result *= m for m in [n-k+1..n] result nCk = (n, k) -> return 1 if k = 0 k_fact = 1 k_fact *= m for m in [1..k] nPk(n, k) / k_fact spatial_entropy = (match) -> if match.graph in ['qwerty', 'dvorak'] s = KEYBOARD_STARTING_POSITIONS d = KEYBOARD_AVERAGE_DEGREE else s = KEYPAD_STARTING_POSITIONS d = KEYPAD_AVERAGE_DEGREE possibilities = 0 L = match.token.length t = match.turns #      L,  t     for i in [2..L] possible_turns = Math.min(t, i – 1) for j in [1..possible_turns] possibilities += nCk(i – 1, j – 1) * s * Math.pow(d, j) entropy = lg possibilities #   ,     # (%  5, A  a) #     ,  #        # . .   if match.shifted_count S = match.shifted_count U = match.token.length – match.shifted_count #     possibilities = 0 possibilities += nCk(S + U, i) for i in [0..Math.min(S, U)] entropy += lg possibilities entropy 

:

 dictionary_entropy = (match) -> entropy = lg match.rank entropy += extra_uppercasing_entropy match entropy += extra_l33t_entropy match entropy 

— : : , the good , photojournalist maelstrom — . zxcvbn , , , . , correcthorsebatterystaple xkcd zxcvbn (45,2 44 ). xkcd 211 ( 2000 ), zxcvbn . zxcvbn.js , , , .
, «», , . , , :

 extra_uppercase_entropy = (match) -> word = match.token return 0 if word.match ALL_LOWER #       —  #    , #          ( + # ): #  1   . #           #   , #     ,   , #   ,  1  for regex in [START_UPPER, END_UPPER, ALL_UPPER] return 1 if word.match regex #   ,      #   # U+L     U    # ,   ,   (, PASSwORD), —  #      U+L   L    U = (chr for chr in word.split(”) when chr.match /[AZ]/).length L = (chr for chr in word.split(”) when chr.match /[az]/).length possibilities = 0 possibilities += nCk(U + L, i) for i in [0..Math.min(U, L)] lg possibilities 

, 1 « » . , :


l33t , .

, , zxcvbn . — : :

 dictionary_match = (password, ranked_dict) -> result = [] len = password.length password_lower = password.toLowerCase() for i in [0...len] for j in [i...len] if password_lower[i..j] of ranked_dict word = password_lower[i..j] rank = ranked_dict[word] result.push( pattern: 'dictionary' i: i j: j token: password[i..j] matched_word: word rank: rank ) result 

Ranked_dict . , , . l33t , dictionary_match. (, bvcxz) , . . matching.coffee github .

Data

, 10 000 , 2011 .

2000 , . zxcvbn Internet Explorer 7, 80 % (. . 80 % , ), — 90 %.

40 000 Wiktionary , 29 . , . , , , (, ), — . , , Frasier 824- .

Conclusion

, , . , — , « » , ( ) . , , . : , , , ( , ).

, . Zxcvbn , ; n-; ; (, qzwxec) . (, ) , , zxcvbn, , — . :

• zxcvbn , . . zxcvbn . .
• , , . zxcvbn , « » , . n- Google , , . , Google.
• Zxcvbn ( ) . ( , ). , — , l33t.

, , , zxcvbn , . , . «» github !
, , , , , , , , , , , , , , .

ABBYY Language Services

ps « », « » — .