The passage of the sapper. Part 2.
After the publication of the topic a lot of interesting, useful and pleasant comments were received. Due to this, I continued to study the issue, redid the calculation algorithm and got some interesting facts (including probabilities of winning with a different number of mines) that I think will interest you.
The brute force advice made me think because I initially did not take it seriously, considering that the search would take a very long time. This would really be the case if mines were moved all over the field. But having downloaded the sapper from IXBT , I realized that it was not necessary at all. It makes sense to consider only those cells that are directly adjacent to open numbers. These numbers do not affect the likelihood of mines in other cells.
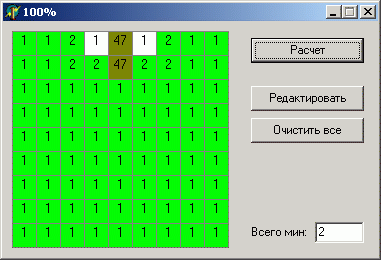
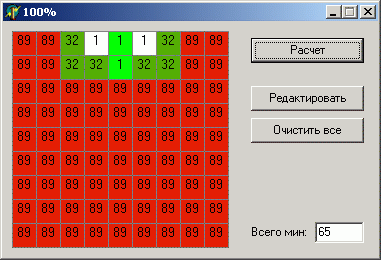
By the way, after studying the downloaded sapper, I found that it completely ignores the remaining number of mines on the field when calculating. At first glance, this is uncritical, since, for example, around a single “4” probability will always be 50/50. But there are cases when the neglect of this factor leads to very bad consequences, for example:
')
The data are absolutely identical, except for the number of mines, but the difference in the result is very significant.
I think you yourself guess why this is happening. There are 2 ways to locate mines: one mine between units (there are no more near) or two mines, one for each unit. If there are 2 mines in the whole field, then one is more likely to be located between units, but the second one can be in almost any cell of the field than both will be near. Conversely, if there are a lot of mines, then the probability that there will not be a single mine in the area of 6 cells (next to the units) is small.
Now calculation from IXBT:
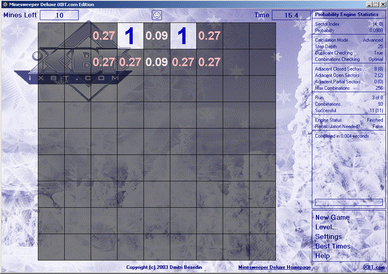
With any number of mines, the probabilities are the same. On the basis of his data, I came to the conclusion that when searching for options, he implies that they are all equally probable, but, as can be seen from the example, this is absolutely not the case.
The calculation of the probability of each case added me a bit of trouble. If in the process of enumeration the option satisfied the conditions, then it was necessary to calculate the probability of this event, and add the resulting number to all the mines (hypothetical mines obtained only for the current variant). Although the calculation itself is not difficult, only the basics of combinatorics are used.
It would be great to finish on this good note, since everything went over perfectly, and the resulting probabilities were fully confirmed by theoretical calculations and the first version of the program. But this is if the number of cells bordering on open numbers was not very large. If the number is over 23, the calculation took more than a second, which was not very pleasant. Therefore, the proven method was adopted (Monte-Carlo, as noted in the previous topic). A random set is generated in the same neighboring cells, which made it possible to increase the number of iterations from 10 thousand to a million. Unfortunately, in difficult cases, an error is still issued, but this happens much less frequently. But in general, it works accurately and quickly. Download here .
When the program was ready, it became interesting to check the frequency of winning on the number of mines. Games were held from one thousand to one million, depending on the complexity and time. The diagram shows only the numbers from 1 to 32, so further the probability becomes very small. The rest is below.
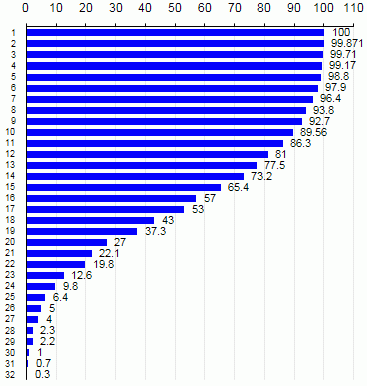
As you can see, the function is fairly smooth. I tried to find an empirical formula for it, but so far to no avail, so it will be great if you tell me.
Especially for M_org , who wondered if I had a weak pass with 64 mines, I drove 10 million times and never won. But now I can safely answer that is not weak even with the 79th :)
The brute force advice made me think because I initially did not take it seriously, considering that the search would take a very long time. This would really be the case if mines were moved all over the field. But having downloaded the sapper from IXBT , I realized that it was not necessary at all. It makes sense to consider only those cells that are directly adjacent to open numbers. These numbers do not affect the likelihood of mines in other cells.
By the way, after studying the downloaded sapper, I found that it completely ignores the remaining number of mines on the field when calculating. At first glance, this is uncritical, since, for example, around a single “4” probability will always be 50/50. But there are cases when the neglect of this factor leads to very bad consequences, for example:


')
The data are absolutely identical, except for the number of mines, but the difference in the result is very significant.
I think you yourself guess why this is happening. There are 2 ways to locate mines: one mine between units (there are no more near) or two mines, one for each unit. If there are 2 mines in the whole field, then one is more likely to be located between units, but the second one can be in almost any cell of the field than both will be near. Conversely, if there are a lot of mines, then the probability that there will not be a single mine in the area of 6 cells (next to the units) is small.
Now calculation from IXBT:

With any number of mines, the probabilities are the same. On the basis of his data, I came to the conclusion that when searching for options, he implies that they are all equally probable, but, as can be seen from the example, this is absolutely not the case.
The calculation of the probability of each case added me a bit of trouble. If in the process of enumeration the option satisfied the conditions, then it was necessary to calculate the probability of this event, and add the resulting number to all the mines (hypothetical mines obtained only for the current variant). Although the calculation itself is not difficult, only the basics of combinatorics are used.
It would be great to finish on this good note, since everything went over perfectly, and the resulting probabilities were fully confirmed by theoretical calculations and the first version of the program. But this is if the number of cells bordering on open numbers was not very large. If the number is over 23, the calculation took more than a second, which was not very pleasant. Therefore, the proven method was adopted (Monte-Carlo, as noted in the previous topic). A random set is generated in the same neighboring cells, which made it possible to increase the number of iterations from 10 thousand to a million. Unfortunately, in difficult cases, an error is still issued, but this happens much less frequently. But in general, it works accurately and quickly. Download here .
The main objective.
When the program was ready, it became interesting to check the frequency of winning on the number of mines. Games were held from one thousand to one million, depending on the complexity and time. The diagram shows only the numbers from 1 to 32, so further the probability becomes very small. The rest is below.

35: 17 ( 10 ) 0.17%
40: 10 ( 100 ) 0.01%
45: 3 ( 100 ) 0.003%
50: 6 ( ) 0.0006%
60: 2 ( ) 0.0002%
70: 0 ( ) ?
75: 6 ( ) 0.0006%
76: 32 ( ) 0.0032%
77: 183 ( ) 0.0183%
78: 1552 ( ) 0.1552%
79: 25350 ( ) 2.535%
As you can see, the function is fairly smooth. I tried to find an empirical formula for it, but so far to no avail, so it will be great if you tell me.
Especially for M_org , who wondered if I had a weak pass with 64 mines, I drove 10 million times and never won. But now I can safely answer that is not weak even with the 79th :)
Source: https://habr.com/ru/post/14923/
All Articles