Monad ContT in Pictures (Haskell)
On Habré already had articles about the continuation and the monad ContT . I decided to share my understanding of this issue and provide it with relevant illustrations. Unlike the above article, I would like to pay more attention to the internal structure of the monad ContT and figure out how it works.
To begin, take a look at the definition of ContT .
Looking at the type, somehow immediately becomes uncomfortable. And the type of callCC becomes even more uncomfortable.
')
Let's figure it out.
For a start it is worth noting that if you have a variable of the type "(a-> mr) -> m r", then it is almost the same as if you had a variable of the type "a". Look here. Suppose you have a variable of type “a” and a function “a-> mr”. You can apply one to the other and get the result "mr":
Now imagine that you have a type variable "(a-> mr) -> m r" and the function "a -> mr". You can also apply one to the other and get your result:
We turn to the pictures.
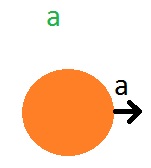
With such a circle with an arrow we will denote some object of type “a”
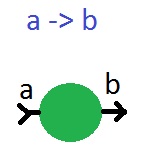
A function like “a-> b” will look like a circle that has an input and an output:
Then our ContT will look like a ring:

If we apply the function "a-> b" to the object "(a-> mr) -> m r", we get the following:

And now the most important thing. We remember that ContT is a monad, so the return and bind functions are defined for it. Let's see what they do.
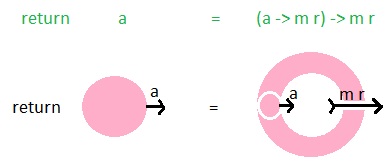
With return, it's pretty simple. It substitutes the object in the passed function, and the result directly returns outside.
This is how bind works.

As you can see, one ring was invested in another. Those. each new calculation is embedded in the previous one. There is something to think about. The current calculation gets all subsequent calculations as a function. This means that it can call this function to calculate the result. Or call it several times, and combine the results. Or maybe not call at all, but immediately return the result.
Suppose we need to open a file, read the name of another file in it, then open it, read the name of the third file in it, open the third file and display the contents on the screen. Usually we would write something like this.
Here you can see how indents increase with each new open file. It would be great to rewrite this piece so that all files open inside one monad. Let's look at the withFileContent function. We see that its type is very similar to the ContT type. Let's now rewrite our example using the ContT monad.
So much more beautiful. Guess how this program will work? The files will first open in the specified sequence, then the result will be displayed on the screen, and then the files will be closed in reverse order. Isn't it great!
Suppose, to work with some object, we need to first call the constructor for it, and after work, the destructor. Create a type class for such objects.
Create some test object.
We write a function withConstructed to work with such objects in ContT . Now they will automatically be called constructors and destructors (in reverse order).
The previous examples were fairly simple and, in fact, the same. And how can we with the help of ContT return some result without waiting for the end of the calculations? Consider an example. Suppose there is some calculation in ContT .
Rewrite calc as follows
We did not change anything, we simply removed the constructor, and then wrapped it in the constructor again.
Now add the line.
The result is still not changed. Not surprising, since the string "ContT $ \ c -> c 5" is equivalent to the string "return 5".
And now the most difficult. Let's replace “c” with “k”.
We see that the result is now equal to 5. It is rather difficult to explain what happened here, but I will try. Consider drawing.

The orange ring is our local variable “c”. These are the calculations that go after the line "ContT $ \ c -> k 5". The green circle is our “k” variable. If we look further through the code, we will see that “k” is nothing more than a print function.
Thus, we pass our value "5" to the variable "c", which in turn uses the print function to display the result on the screen. If we replace “c” with “k”, we get the following picture.

Now we ignore all subsequent calculations and immediately pass the value "5" to the "print" function.
Further, I will no longer change the behavior of the program, but will simply produce equivalent code conversions. To begin with, "we will take out for brackets" our constant "5".
We put out the lambda "(\ a -> ContT $ \ c -> ka)".
Now we will render the whole expression "\ exit -> do ... return z".
It would be necessary to create a separate function with the body "(\ f -> ContT ... ka)) k)". By the way, congratulations! We just invented thebike callCC feature.
The program, of course, turned out absolutely stupid, for that we have learned how to interrupt the calculations.
I tried to deduce the body of the getCC function in the same way and realized that there was already not enough brains for it. Maybe you will succeed.
Contt inside
To begin, take a look at the definition of ContT .
newtype ContT rma = ContT {runContT :: ((a -> mr) -> mr)} Looking at the type, somehow immediately becomes uncomfortable. And the type of callCC becomes even more uncomfortable.
')
callCC :: ((a -> mb) -> ma) -> ma Let's figure it out.
For a start it is worth noting that if you have a variable of the type "(a-> mr) -> m r", then it is almost the same as if you had a variable of the type "a". Look here. Suppose you have a variable of type “a” and a function “a-> mr”. You can apply one to the other and get the result "mr":
a -> mr $ a = mr Now imagine that you have a type variable "(a-> mr) -> m r" and the function "a -> mr". You can also apply one to the other and get your result:
(a -> mr) -> mr $ (a -> mr) = mr We turn to the pictures.
With such a circle with an arrow we will denote some object of type “a”

A function like “a-> b” will look like a circle that has an input and an output:

Then our ContT will look like a ring:

If we apply the function "a-> b" to the object "(a-> mr) -> m r", we get the following:

And now the most important thing. We remember that ContT is a monad, so the return and bind functions are defined for it. Let's see what they do.
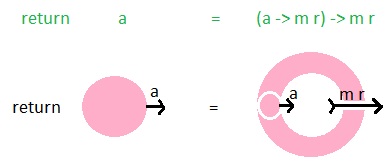
With return, it's pretty simple. It substitutes the object in the passed function, and the result directly returns outside.
This is how bind works.

As you can see, one ring was invested in another. Those. each new calculation is embedded in the previous one. There is something to think about. The current calculation gets all subsequent calculations as a function. This means that it can call this function to calculate the result. Or call it several times, and combine the results. Or maybe not call at all, but immediately return the result.
Examples
Work with files
Suppose we need to open a file, read the name of another file in it, then open it, read the name of the third file in it, open the third file and display the contents on the screen. Usually we would write something like this.
withFileContent :: FilePath -> (String -> IO a) -> IO a withFileContent file fun = withFile file ReadMode $ \h -> hGetContents h >>= fun main = do withFileContent "1.txt" $ \file1_content -> do withFileContent file1_content $ \file2_content -> do withFileContent file2_content $ \file3_content -> do print file3_content Here you can see how indents increase with each new open file. It would be great to rewrite this piece so that all files open inside one monad. Let's look at the withFileContent function. We see that its type is very similar to the ContT type. Let's now rewrite our example using the ContT monad.
doContT cont = runContT cont (const $ return ()) main = doContT $ do file1_content <- ContT $ withFileContent "1.txt" file2_content <- ContT $ withFileContent file1_content file3_content <- ContT $ withFileContent file2_content liftIO $ print file3_content So much more beautiful. Guess how this program will work? The files will first open in the specified sequence, then the result will be displayed on the screen, and then the files will be closed in reverse order. Isn't it great!
Constructors, destructors
Suppose, to work with some object, we need to first call the constructor for it, and after work, the destructor. Create a type class for such objects.
class Constructed a where constructor :: a -> IO () destructor :: a -> IO () Create some test object.
newtype Obj a = Obj a instance (Show a) => Constructed (Obj a) where constructor (Obj a) = putStr $ "constructor for " ++ (show a) ++ "\n" destructor (Obj a) = putStr $ "destructor for " ++ (show a) ++ "\n" We write a function withConstructed to work with such objects in ContT . Now they will automatically be called constructors and destructors (in reverse order).
withConstructed :: (Constructed a) => a -> ContT r IO a withConstructed obj = ContT $ \fun -> do constructor obj rez <- fun obj destructor obj return rez main = doContT $ do a <- withConstructed $ Obj "ObjectA" b <- withConstructed $ Obj "ObjectB" c <- withConstructed $ Obj "ObjectC" liftIO $ putStr "do something\n" {- : constructor for "ObjectA" constructor for "ObjectB" constructor for "ObjectC" do something destructor for "ObjectC" destructor for "ObjectB" destructor for "ObjectA" -} Interrupt computing
The previous examples were fairly simple and, in fact, the same. And how can we with the help of ContT return some result without waiting for the end of the calculations? Consider an example. Suppose there is some calculation in ContT .
calc :: ContT rm Int calc = do x <- return 10 y <- return $ x*2 z <- return $ x + y return z main = runContT calc print -- : 30 Rewrite calc as follows
calc = ContT $ \k -> runContT (do -- <- / x <- return 10 y <- return $ x*2 z <- return $ x + y return z) k main = runContT calc print -- : 30 We did not change anything, we simply removed the constructor, and then wrapped it in the constructor again.
Now add the line.
calc = ContT $ \k -> runContT (do x <- return 10 y <- return $ x*2 ContT $ \c -> c 5 -- <- ( "return 5") z <- return $ x + y return z) k main = runContT calc print -- : 30 The result is still not changed. Not surprising, since the string "ContT $ \ c -> c 5" is equivalent to the string "return 5".
And now the most difficult. Let's replace “c” with “k”.
calc = ContT $ \k -> runContT (do x <- return 10 y <- return $ x*2 ContT $ \c -> k 5 -- <- "c" "k" z <- return $ x + y return z) k main = runContT calc print -- <- "print" ContT -- : 5 -- <- We see that the result is now equal to 5. It is rather difficult to explain what happened here, but I will try. Consider drawing.

The orange ring is our local variable “c”. These are the calculations that go after the line "ContT $ \ c -> k 5". The green circle is our “k” variable. If we look further through the code, we will see that “k” is nothing more than a print function.
Thus, we pass our value "5" to the variable "c", which in turn uses the print function to display the result on the screen. If we replace “c” with “k”, we get the following picture.

Now we ignore all subsequent calculations and immediately pass the value "5" to the "print" function.
Further, I will no longer change the behavior of the program, but will simply produce equivalent code conversions. To begin with, "we will take out for brackets" our constant "5".
calc = ContT $ \k -> runContT (do x <- return 10 y <- return $ x*2 (\a -> ContT $ \c -> ka) 5 -- <- "a" z <- return $ x + y return z) k We put out the lambda "(\ a -> ContT $ \ c -> ka)".
calc = ContT $ \k -> runContT ((\exit -> do -- <- "exit" x <- return 10 y <- return $ x*2 exit 5 z <- return $ x + y return z) (\a -> ContT $ \c -> ka)) k Now we will render the whole expression "\ exit -> do ... return z".
calc = (\f -> ContT $ \k -> runContT (f (\a -> ContT $ \c -> ka)) k) $ \exit -> do -- ^ "f" x <- return 10 y <- return $ x*2 exit 5 z <- return $ x + y return z It would be necessary to create a separate function with the body "(\ f -> ContT ... ka)) k)". By the way, congratulations! We just invented the
callCC f = ContT $ \k -> runContT (f (\a -> ContT $ \_ -> ka)) k calc = callCC $ \exit -> do -- <- "callCC" x <- return 10 y <- return $ x*2 exit 5 z <- return $ x + y return z The program, of course, turned out absolutely stupid, for that we have learned how to interrupt the calculations.
PS
I tried to deduce the body of the getCC function in the same way and realized that there was already not enough brains for it. Maybe you will succeed.
Source: https://habr.com/ru/post/149174/
All Articles