Cyberpunk, matrices and canvas

I. Preface.

Once upon a time I had a crush on the episode from the cyberpunk novel: one hero shows another screen, on which pixels quickly replace each other. Each screen state is represented by a certain number, the program gradually sorts through the options.

One can imagine that sooner or later various amazing things could appear on this screen: a page from “War and Peace”, “Gioconda”, the first bars of the “Moonlight Sonata”, a brilliant solution of a known equation, a photo of any person, this Habr's page, a message about an unknown event of the past or a detailed prediction of the future.
')
Since then, I occasionally tried to do something tangentially, there were some small crafts on Perl. And recently I wanted to do something similar in JavaScript.

Ii. Terms of implementation.

Implementing such a brute force and its graphical display is easy. Here are the available scales will be quite small.

Suppose for simplicity that each point of the screen is represented by two states - white and black, which corresponds to zero and one in the binary representation of a number. The consecutive coordinates of the points correspond to the ordinal position of the digit in the number.

Currently, the maximum integer in JavaScript with the same accuracy of calculations is 2 to the power of 53. Math.pow(2,53) == Math.pow(2,53) + 1 gives true . This number is represented by 54 binary positions:

 0b100000000000000000000000000000000000000000000000000000 0x20000000000000 9007199254740992 

The matrix will correspond to the number of only 9 to 6 pixels. Suppose my computer can do about 50 million operations per second. In order to sort through all the variants of the matrix, he will need it by rough calculations.

Math.pow(2,53) / 50000000 / 60 / 60 / 24 / 365 - about six years.

A stronger computer will need less, but a person will not be able to analyze at such a speed limit. Assume that the matrix states will replace each other with the traditional television broadcasting frequency - 25 frames per second. Then, in order to go through all the states of a tiny piece of 2D black and white reality with visual speed, we will need 1,428,082 years.

And yet it is interesting to create something like this. The maximum number mentioned is not very convenient for this, because when the left upper point becomes one (it is repainted black), nothing more can be drawn on this matrix. Therefore, we will never be able to fully use the extreme upper and left lines in our micrograph. Therefore, we take a slightly smaller number, the matrix of which can be completely filled with black color, can take really any states and have a relatively proportional form. This will be a 10 by 5 matrix with a maximum number of 50 binary orders:

 parseInt( "1111111111" + "1111111111" + "1111111111" + "1111111111" + "1111111111" , 2) 

 0b11111111111111111111111111111111111111111111111111 0x3ffffffffffff 1125899906842623 

All further implementations have been successfully tested on the latest versions of Chrome, Firefox, Opera and Safari. Unfortunately, on the ninth IE, I can not test, and on the eighth only examples without the use of canvas will work.

You can save any matrix, edit the code if necessary, and run it locally.

I understand that everything further looks like a kindergarten. Therefore, I ask for indulgence to a person with a humanitarian mindset, trying to play other people's toys. All this is just for (slightly metaphysical) fun :)

Iii. Sequential matrix

Since the matrix is ​​very small, it is not very convenient and clear to implement it on pixel graphics, so for simplicity and ease of scaling we will have a simple table of 10 by 5 cells with variable color. The first order is in the lower right corner.

To begin with, I wrote a graphics to number converter for such a matrix. Each mouse click on a cell changes color and accordingly switches the order in the number between one and zero. Above the sign the number itself is displayed in decimal format. Cell size in pixels can be set with the scale parameter in the page address.

Converter

It remains to write the matrix itself with a successive change of states. It will be the same table, but with a different behavior. So that nothing distracts on the page from the purity of the presentation, the control in this and the following handicrafts will be distributed between the mouse and the parameters in the URL.

Our matrix has three parameters with the following defaults:

scale=10 - the already mentioned cell size in pixels;
fps=25 - frame rate per second;
start=1 - the number with which the search starts.

Each click of the mouse increases the number by one and changes the state of the matrix. If you click with the Ctrl key Ctrl , the automatic search will be started / stopped. The current number is displayed in the title of the document (window, tab).

10x5 sequential matrix

Say, between a state that displays a graphic unit :



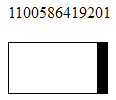
and the state representing the graphic deuce :



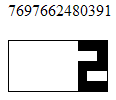
passes 7697662480391 - 1100586419201 = 6597076061190 frames. With FPS, the default is about 8368 years of contemplation :)

The higher and to the left is the point, the more time passes before it appears.

You can, for example, see how the main answer to the main question turns little by little into some other answer .

Iv. Random matrices.

1. One number.

Our sequential search matrix can be converted into a matrix that iterates through random values. The parameter of the initial number loses its meaning, otherwise everything remains the same (except that we have reduced the frame rate to 1 per second by default, otherwise illegible fading will occur).

One of the random states, oddly enough - with a perfect letter A:



10x5 random matrix

2. Sets of numbers.

In order to somehow diversify our matrix reality, let us go beyond the bounds of searching for a single number. We will create matrices that are not limited in size. Their states will be set by a set of random numbers according to different principles. We will implement them using canvas.

but. Random whole images.

Here each frame of the matrix will be completely different from the other. Each point of the frame is given by one random number. Let us analyze the default parameters (previous and future links include these parameters for clarity: these settings are used if no parameters are set).

w=400 - matrix width in pixels
h=300 - matrix height in pixels
fps=1 - frame rate

As before, one click of the mouse replaces one frame. Clicking with the Ctrl key launches a random state transition. But now some more possibilities are added.

When you click the middle mouse button in a new tab or in a new window, a copy of the matrix in PNG format opens, if you need to save a picture for some reason (by the way, all the following illustrations are obtained in this way).

Shift click the left button toggles the color depth of the picture: black and white, grayscale, color mode. If you hold down the Shift+Alt keys, the switching is performed in the reverse order.

Of course, the randomness of each point means that in the overwhelming majority of states we will get graphical noise like a screen of an unconfigured TV. After all, alternations are distributed in such a space relatively evenly. However, people with rich imagination and sensitive perception can see interesting plots in this noise or unexpectedly recall something exciting because of whimsical associations.







Random images

b. Random points.

In this kind of matrix, random points are sequentially added to the constant background. Let's enter one more parameter:

bg=w - background color (w - white (white), b - black (black)). Another color mode is also added, there are four of them now: monochrome (black or white dots on the opposite background; sooner or later they can fill the entire canvas and the state will no longer change visually) and the previous three modes (they don’t fill them, because in black and white, the previous state can be painted over with a new one).

Dots appearing on a black background in the mode of shades of gray or color are similar to the lighting stars of different brightness.



And if you make the background white, start the animation and zoom in on the page, with time you can play a game that is often found in children's magazines: connect the dots to make a picture. True picture will not be known in advance.

Random points

at. Random lines.

In this kind of matrix, random lines are constantly added to the background. I remember that at school we often played another similar game: a blank sheet is taken, one player draws an arbitrary pattern on it without looking, then the other players take turns circling the images they see in different colors. Patterns appear on our matrix, similar to the starting fields of this game.

To the old factors of randomness (coordinates of points and color) two more are added. New parameters are responsible for them:

lines=r - type of lines (can take three values: s - only straight (straight), c - only curves (curve), r - random alternation of straight lines and curves (random); when drawing curves to two random points of the beginning and end of the segment add two more random points that control the bend - the usual parameters for Bezier curves);

traverse=r - drawing method (also takes three values: y - draw without taking your hand off the paper (yes), n - each time start a line from a new random point (no), r - a random alternation of separation with a continuous extension (random) ).

The previous four color modes remain here.





Random lines

Random figures.

Now we will close the lines and paint them. Random “strokes” will be obtained. The traverse parameter loses its meaning, but new three random factors with their parameters are added.

alpha=y - randomly change the level of color transparency (two values, y (yes) or n (no), respectively, to use transparency or not). When using transparency, the first three modes of color depth (monochrome, black and white and shades of gray) become very similar to each other.

minnodes=3 - the minimum number of nodes in the figure

maxnodes=10 - the maximum number of nodes in the figure.

By default, the restrictions are set to 3 (it makes no sense to install less, because the figures will not work) to 10 (this upper limit can be edited in the code). The shape of the figures is also greatly influenced by the already described lines parameter (polygons or more complex shapes are obtained respectively). It should be noted that the figures will often be self-intersecting, so the fill will be difficult, with a variety of spaces.

The following are examples of different color modes on a different background, using transparency and without using the alpha channel.













Random shapes

You can also combine all the described types of drawing (fragments of whole images, points, lines, shapes). This game with the code I give to those interested. Thank you all so much for your attention :)

References to all described matrices .