As I wrote the MIDI keyboard
Not long ago, I had the idea to write my own MIDI keyboard. Later a guitar neck was bolted to it, she learned to recognize chords and play melodies. Actually about this will be this post.
If you are interested in how to programmatically play sound through MIDI synthesizers, guitar chord recognition algorithm, or you just love to play the guitar or keyboard instruments, please use Cat.
Before you write the keyboard you need to somehow learn how to play the sound. The first thing that comes to mind is to use a synthesizer built into the system. It is on every device, and you do not need to install anything. In general, it works out of the box.
I decided to write the program on C #. Searching in Google, I found out that .NET itself cannot work with MIDI, but there are WinAPI functions for that. A subsequent search eventually led me to the NAudio library. With it, we will play sounds.
To play a note, you need to send a specific message to MidiOut, with the indication of the playback channel, note and force.
For example, you can play the note of the 3rd octave:
')
But not everything is so simple, you need to stop playing the note, otherwise it will sound like that.
Before playing you need to open the desired MIDI device. This is done by simply creating the MidiOut object. The device number is transferred to the constructor, because there may be several of them.
You can find out their number by reading the static property MidiOut.NumberOfDevices, and get information about this device using the MidiOut.DeviceInfo method, passing it the identifier of the synthesizer.
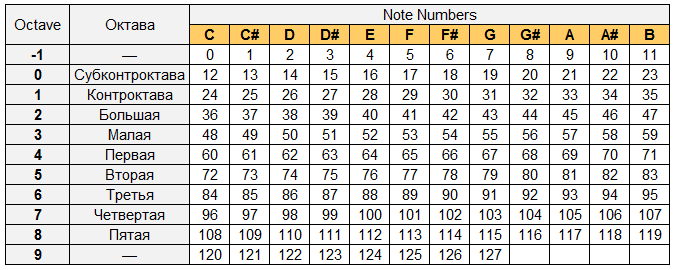
Remember that strange number 57? This is the note ID. The numbering starts from 0, each following value is an increase in tonality by a semitone.
The dependence of the played note on the ID can be seen on the table:
After reviewing all this information, I wrote a class to simplify working with NAudio:
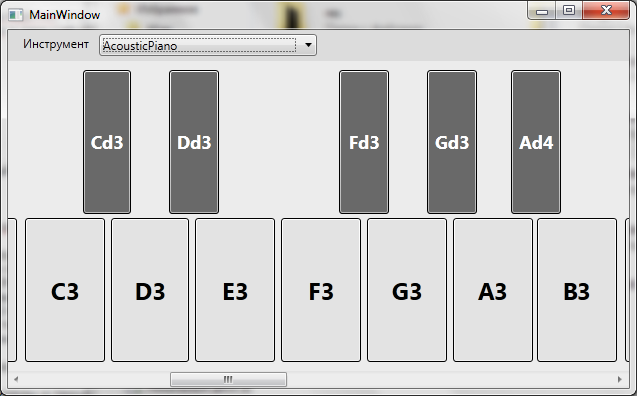
And also made a trial version of the MIDI-keyboard
The next stage is the creation of a guitar neck and binding notes to strings and frets.
Guitar neck is very simple. Each string in the open position produces a sound with a specific tone. The same string, clamped on a certain fret, makes a sound several tones above (1 fret - 1 semitone).
If the open string makes an E4 sound, then it is clamped on the second fret and makes the sound F # 4, and on the 12th, E5.
The algorithm is simple: we take the note of an open string, and increase it by a certain number of semitones.
To simplify my life, I wrote a class:
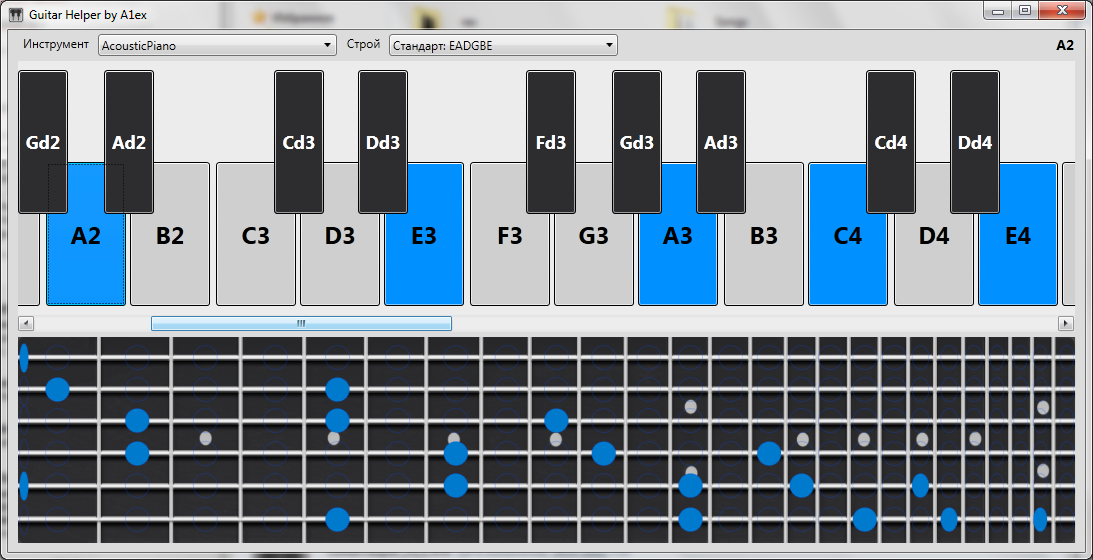
Here's what I got at this stage:
This stage is also not particularly difficult except for one moment, which will be described a little later.
It is a little theory: a chord is a set of sounds of certain keys. These notes are not taken anyhow - they are located at certain intervals. Intervals are measured in semitones.
Accord in A minor, for example, has intervals of 3.4, i.e. represents a sequence of notes: A, C, E (For, do, mi)
I can’t tell you more about this, because Amateur in music, conservatories did not finish. And I'm afraid to tell a lot of things too much and far from the truth. More can be found on Wikipedia .
Let's go back to the program.
The recognition algorithm is as follows:
It would be possible to finish this if it were not for one thing: guitar chords are not as simple as we would like. They contain many sounds of a certain scale. For example, the guitar in A minor contains already 5 sounds, even though these are the same la-domi.
This complicates recognition:
As you probably already guessed, I also created a class to simplify working with chords:
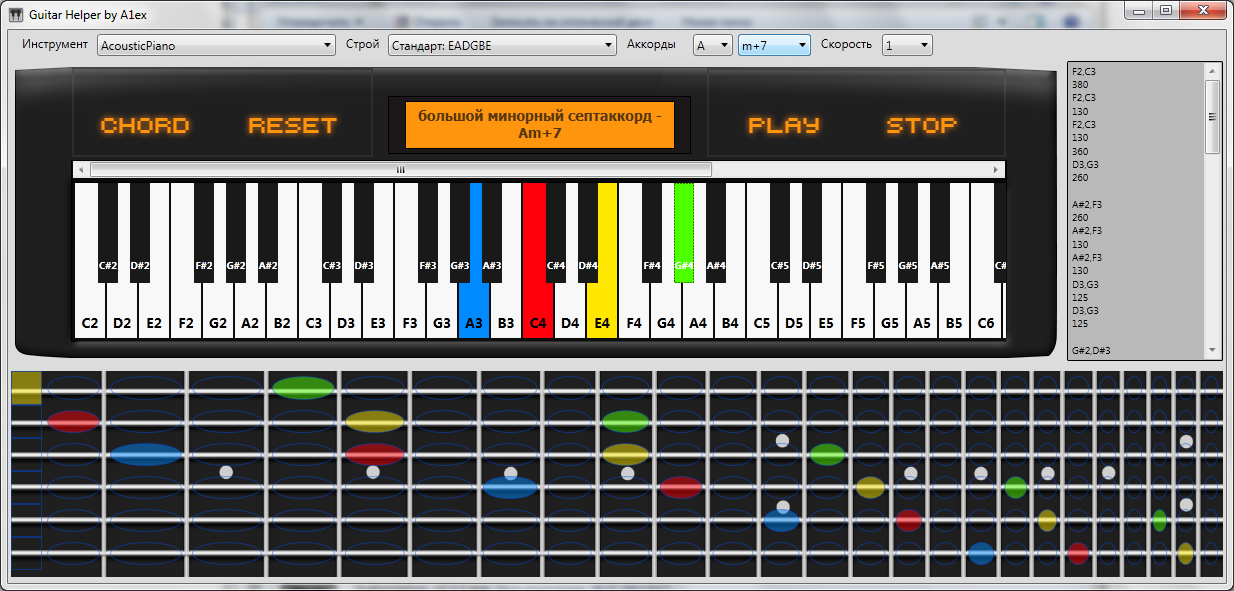
Final result:
Full project source codes are available on GitHub .
I also want to thank Comrade Sadler , author of the post “Ovation. Do-it-yourself chord table using JS and HTML5 ” , in which I spied on the chord table. It saved me a bit of time.
If you are interested in how to programmatically play sound through MIDI synthesizers, guitar chord recognition algorithm, or you just love to play the guitar or keyboard instruments, please use Cat.
One, two or three ...
Before you write the keyboard you need to somehow learn how to play the sound. The first thing that comes to mind is to use a synthesizer built into the system. It is on every device, and you do not need to install anything. In general, it works out of the box.
I decided to write the program on C #. Searching in Google, I found out that .NET itself cannot work with MIDI, but there are WinAPI functions for that. A subsequent search eventually led me to the NAudio library. With it, we will play sounds.
To play a note, you need to send a specific message to MidiOut, with the indication of the playback channel, note and force.
For example, you can play the note of the 3rd octave:
midiOut.Send( MidiMessage.StartNote( 57, 127, 0 ).RawData ) //id , (0-127), ; ')
But not everything is so simple, you need to stop playing the note, otherwise it will sound like that.
midiOut.Send( MidiMessage.StopNote( 57, 0, 0 ).RawData ); Before playing you need to open the desired MIDI device. This is done by simply creating the MidiOut object. The device number is transferred to the constructor, because there may be several of them.
You can find out their number by reading the static property MidiOut.NumberOfDevices, and get information about this device using the MidiOut.DeviceInfo method, passing it the identifier of the synthesizer.
Remember that strange number 57? This is the note ID. The numbering starts from 0, each following value is an increase in tonality by a semitone.
The dependence of the played note on the ID can be seen on the table:

After reviewing all this information, I wrote a class to simplify working with NAudio:
Hidden text
internal struct Note { public Note( byte oct, Tones t ) { octave = oct; tone = t; id = 12 + octave * 12 + (int)tone; } public byte octave; public Tones tone; public int id; } public enum Tones { A = 9, Ad = 10, B = 11, C = 0, Cd = 1, D = 2, Dd = 3, E = 4, F = 5, Fd = 6, G = 7, Gd = 8 } class AudioSintezator : IDisposable { public int PlayTone( byte octave, Tones tone ) { // 12 , 0- ( -1-) int note = 12 + octave * 12 + (int)tone; if( !playingTones.Contains( note ) ) { // . 0 midiOut.Send( MidiMessage.StartNote( note, 127, 0 ).RawData ); playingTones.Add( note ); } return note; } public void StopPlaying( int id ) { if( playingTones.Contains( id ) ) { // midiOut.Send( MidiMessage.StopNote( id, 0, 0 ).RawData ); playingTones.Remove( id ); } } MidiOut midiOut = new MidiOut( 0 ); List<int> playingTones = new List<int>(); public void Dispose() { midiOut.Close(); midiOut.Dispose(); } } And also made a trial version of the MIDI-keyboard

Sex, drugs and rock and roll
The next stage is the creation of a guitar neck and binding notes to strings and frets.
Guitar neck is very simple. Each string in the open position produces a sound with a specific tone. The same string, clamped on a certain fret, makes a sound several tones above (1 fret - 1 semitone).
If the open string makes an E4 sound, then it is clamped on the second fret and makes the sound F # 4, and on the 12th, E5.
The algorithm is simple: we take the note of an open string, and increase it by a certain number of semitones.
To simplify my life, I wrote a class:
Hidden text
class Guitar { public Guitar( params Note[] tune ) { for( int i = 0; i < 6; ++i ) { strs.Add( new GuitarString( tune[i] ) ); } } public List<Tuple<byte, byte>> GetFretsForNote( Note note ) { // 1- ( 0 5), 2- - ( 0 - ) List<Tuple<byte, byte>> result = new List<Tuple<byte, byte>>(); byte currentString = 0; foreach( var str in strs ) { var fret = str.GetFretForNote( note ); if( fret != -1 ) // { result.Add( new Tuple<byte, byte>( currentString, (byte)fret ) ); } ++currentString; } return result; } public Note GetNote( byte str, byte fret ) { return strs[str].GetNoteForFret( fret ); } public void SetTuning( params Note[] tune ) // { for( int i = 0; i < 6; ++i ) { strs[i].SetTune( tune[i] ); } } List<GuitarString> strs = new List<GuitarString>(); } class GuitarString { public GuitarString( Note note ) { this.open = note; } public void SetTune( Note note ) { this.open = note; } public Note GetNoteForFret( byte fret ) { return open + fret; } public int GetFretForNote( Note note ) { int fret = -1; // -1 , if( open <= note ) { int octDiff = note.octave - open.octave; int noteDiff = note.tone - open.tone; fret = octDiff * 12 + noteDiff; } return fret; } Note open; } Here's what I got at this stage:

Triads, septa chords and other joys of music
This stage is also not particularly difficult except for one moment, which will be described a little later.
It is a little theory: a chord is a set of sounds of certain keys. These notes are not taken anyhow - they are located at certain intervals. Intervals are measured in semitones.
Accord in A minor, for example, has intervals of 3.4, i.e. represents a sequence of notes: A, C, E (For, do, mi)
I can’t tell you more about this, because Amateur in music, conservatories did not finish. And I'm afraid to tell a lot of things too much and far from the truth. More can be found on Wikipedia .
Let's go back to the program.
The recognition algorithm is as follows:
- Find the lowest sound, it will be the base for the chord (tonic, if not mistaken)
- We consider the intervals between the "neighboring" notes
- We are checking with the table of intervals prepared in advance.
It would be possible to finish this if it were not for one thing: guitar chords are not as simple as we would like. They contain many sounds of a certain scale. For example, the guitar in A minor contains already 5 sounds, even though these are the same la-domi.
This complicates recognition:
- Create a list of notes, removing from it duplicate sounds (up to different octaves, for example)
- We move them closer, removing distances in an octave, or even several
- We check according to the table of intervals. If you do not find a match, then go ahead
- We look through all possible combinations (permutations) and check the table.
- If you still have not found, then we call the chord unknown.
As you probably already guessed, I also created a class to simplify working with chords:
Hidden text
static class Chords { public static ChordType[] chordTypes = new ChordType[]{ new ChordType(" ", "", 4,3), new ChordType(" ", "m", 3,4), new ChordType(" ", "5+", 4,4), new ChordType(" ", "m-5", 3,3), new ChordType(" ", "maj7", 4,3,4), new ChordType(" ", "m+7", 3,4,4), new ChordType("", "7", 4,3,3), new ChordType(" ", "m7", 3,4,3), new ChordType(" ", "maj5+", 4,4,3), new ChordType(" ", "m7-5", 3,3,4), new ChordType(" ", "dim", 3,3,3), new ChordType(" (IV)", "sus2", 2,5), new ChordType(" (II)", "sus4", 5,2), new ChordType("","6", 4,3,2), new ChordType("", "m6", 3,4,2), new ChordType(" ", "9", 4,3,3,4), new ChordType(" ", "m9", 3,4,3,4), new ChordType(" ", "-9", 4,3,3,3), new ChordType(" ", "m-9", 3,4,3,3), new ChordType("",""), new ChordType(" ", " - 2", 1), new ChordType(" ", " - 2", 2), new ChordType(" ", " - 3", 3), new ChordType(" ", " - 3", 4), new ChordType(" ", " - 4", 5), new ChordType(" ", " - 4", 6), new ChordType(" ", " - 5", 7), new ChordType(" ", " - 6", 8), new ChordType(" ", " - 6", 9), new ChordType(" ", " - 7", 10), new ChordType(" ", " - 7", 11), new ChordType("", " - ", 12), new ChordType(" ", " - 9", 13), new ChordType(" ", " - 9", 14) }; public static string[] chordsBases = new string[] { "A","A#","B","C","C#","D","D#","E", "F","F#","G","G#" }; public static string[] chordMods = new string[] { "","m","5+","m-5","maj7","m+7","7", "m7","maj5+","m7-5","dim","sus2","sus4", "6","m6","9","m9","-9","m-9" }; private static int GetChordType( List<Note> tmp ) { int[] intervals = new int[tmp.Count - 1]; for( int i = 0; i < tmp.Count - 1; ++i ) { intervals[i] = tmp[i] - tmp[i + 1]; } int type = 0; foreach( var chordType in Chords.chordTypes ) { if( Utils.CompareArrays( intervals, chordType.intervals ) ) break; ++type; } return type; } public static void GetChord( List<Note> chordNotes, out Note BaseNote, out ChordType type ) { List<Note> notes = PrepareNotes( chordNotes ); // int typeIndex = GetChordType( notes ); // if( typeIndex < chordTypes.Length ) // { BaseNote = notes[0]; type = chordTypes[typeIndex]; } else { bool unknown = true; var possibleChord = new List<Note>( notes ); // foreach( List<Note> perm in Utils.GeneratePermutation( possibleChord ) ) { // ( > 12 ) for( int k = 1; k < perm.Count; ++k ) { if( perm[k].tone > perm[k - 1].tone ) { perm[k] = new Note( perm[k - 1].octave, perm[k].tone ); } else { perm[k] = new Note( (byte)(perm[k - 1].octave + 1), perm[k].tone ); } } typeIndex = GetChordType( possibleChord ); if( typeIndex < Chords.chordTypes.Length ) { unknown = false; break; // , } } if( unknown ) { throw new Exception( " " ); } else { BaseNote = possibleChord[0]; type = chordTypes[typeIndex]; } } } private static List<Note> PrepareNotes( List<Note> notes ) { List<Note> tmp = new List<Note>(); bool finded = false; for( int i = 0; i < notes.Count; ++i ) { finded = false; var note = notes[i]; for( int j = 0; j < tmp.Count; ++j ) // { if( note.tone == tmp[j].tone ) { finded = true; break; } } if( !finded ) // { tmp.Add( note ); } } // , if( tmp.Count == 1 && notes.Count > 1 ) return notes; // "" byte lowest = tmp[0].octave; var lowesTone = tmp[0].tone; for( int i = 0; i < tmp.Count; ++i ) { if( tmp[i].octave > lowest ) { if( Utils.CountOfTones( tmp[i].tone, notes ) > 1 ) { if( tmp[i].tone > lowesTone ) { tmp[i] = new Note( lowest, tmp[i].tone ); } else { tmp[i] = new Note( (byte)(lowest + 1), tmp[i].tone ); } } } } tmp = tmp.OrderBy( x => x.id ).ToList(); return tmp; } } Final result:

Full project source codes are available on GitHub .
I also want to thank Comrade Sadler , author of the post “Ovation. Do-it-yourself chord table using JS and HTML5 ” , in which I spied on the chord table. It saved me a bit of time.
Source: https://habr.com/ru/post/148852/
All Articles