Experimental Determination of Cache Memory Characteristics
Due to what we see a constant increase in the performance of single-threaded programs? At the moment we are at that stage of development of microprocessor technologies, when the increase in the speed of single-threaded applications depends only on memory. The number of cores is growing, but the frequency is fixed within 4 GHz and does not give a performance boost.
The speed and frequency of the memory is the main reason why we get “our own piece of free cake” (link). That is why it is important to use memory as efficiently as we can, and even more so as fast as a cache. To optimize the program for a specific computer, it is useful to know the characteristics of the processor's cache memory: the number of levels, size, line length. This is especially important in high-performance code - kernel systems, math libraries.
How to determine the characteristics of the cache automatically? (Naturally, cpuinfo is not considered parsing, though, if only because, ultimately, we would like to get an algorithm that can be easily implemented in other OSes. Convenient, isn't it?) This is what we are going to do now.
')
At the moment, there are three widely used types of cache memory: direct mapping cache, associative cache, and multiple associative cache.

LRU - crowding out the “long unused” line, the memory cache.
To determine the number of cache levels, you need to consider the order of memory accesses, in which the transition is clearly visible. Different cache levels differ primarily in memory responsiveness. In the case of “cache miss” for the L1 cache, data will be searched in the following memory levels, while if the data size is greater than L1 and less than L2, then the speed of the memory response will be the speed of the L2 response. The previous statement is also true in general cases.
It is clear that you need to pick up a test on which, we will clearly see the cache misses and test it on various data sizes.
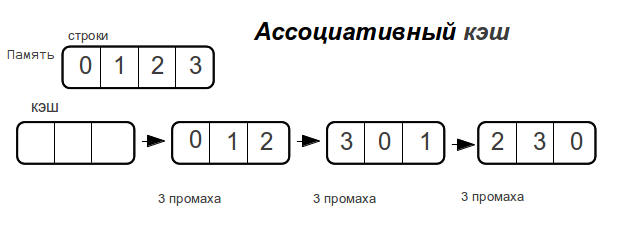
Knowing the logic of multiple-associative caches using the LRU algorithm, it is not difficult to come up with an algorithm on which the cache “crashes”, nothing tricky - passing through the line. The criterion of effectiveness will be considered the time of one memory access. Naturally you need to consistently refer to all elements of the line, repeating repeatedly to averaging the result. For example, there may be cases when the string fits in the cache, but for the first pass we load the string from the RAM and therefore we get completely inadequate time.
I want to see something like steps, passing through rows of different lengths. To determine the character of the steps, consider the example of a row pass for the forward and associative cache, the case with the multiply associative cache will be the average between the forward mapping cache and the associative cache.
Associative cache
As soon as the data size exceeds the cache size,
fully associative cache “misses” every time memory is accessed.
Direct cache
Consider different row sizes. - shows the maximum number of misses that the processor will spend to access the elements of the array during the next pass through the line.

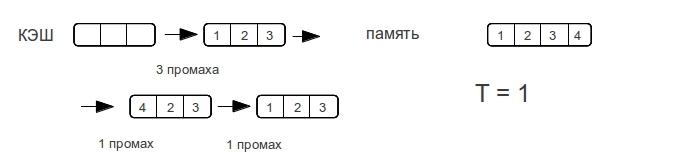
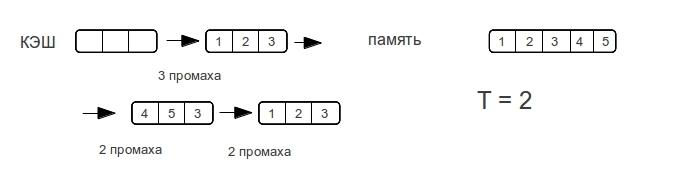
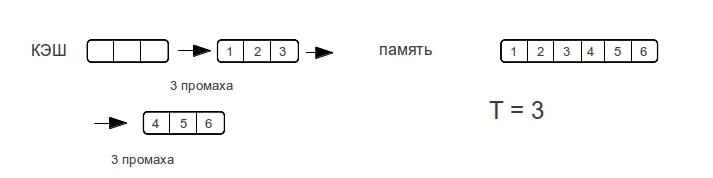
As you can see, the memory access time does not increase dramatically, but as the amount of data increases. As soon as the size of the data exceeds the size of the cache, then there will be misses with each memory access.
Therefore, the associative cache will have a vertical step, while the direct cache will gradually increase up to double the cache size. A multiple associative cache would be a middle case, a “bump”, if only because access time cannot be better than a direct one.
If we talk about memory, the fastest is cache, followed by operational, the slowest is swap, we will not talk about it in the future. In turn, different cache levels (as a rule, processors today have 2-3 cache levels) have different memory response rates: the higher the level, the slower the response speed. And therefore, if the line is placed in the first level of the cache (which is by the way fully associative), the response time will be less than that of the line significantly larger than the sizes of the first level cache. Therefore, on the graph of memory response time from the size of the line there will be several plateaus - a plateau * of memory response, and a plateau caused by different levels of cache.
* The function plateau is {i: x, f (xi) - f (xi + 1) <eps: eps → 0}
For implementation we will use C (ANSI C99).
Quickly written code, the usual passage through the rows of different lengths, less than 10mb, performed many times. (We will give small pieces of the program that carry the meaning).
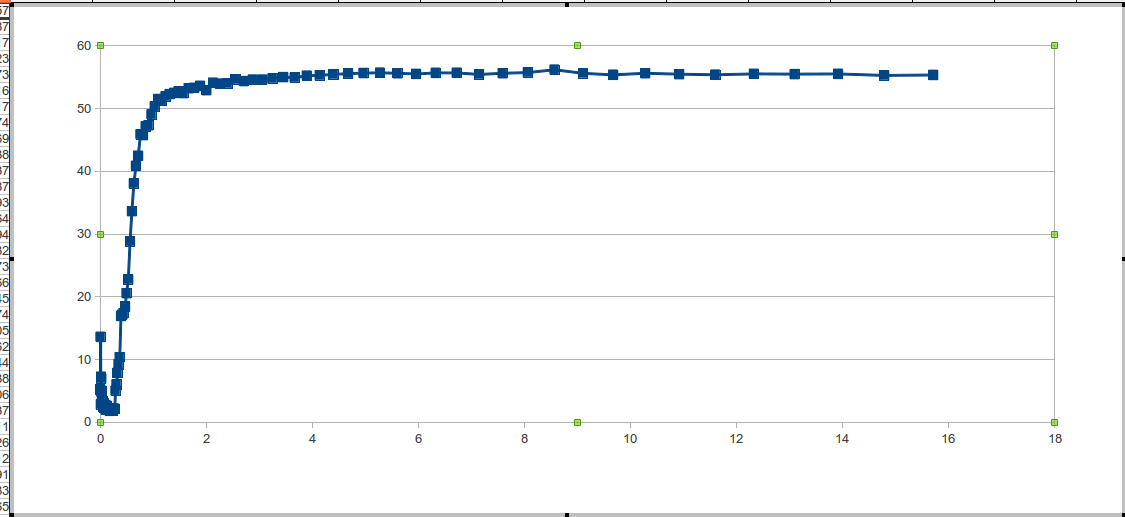
We look at the chart - and we see one big step. But after all, in theory everything turns out, just wonderful. So you need to understand: why is this happening? And how to fix it?
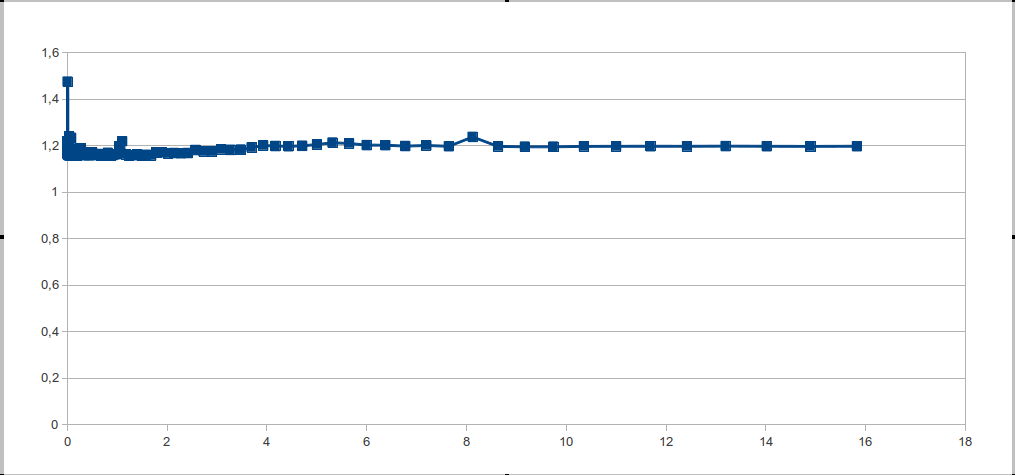
Obviously, this can happen for two reasons: either there is no memory cache in the processor, or the processor guesses memory references so well. Since the first option is closer to fiction, the reason for all is a good prediction of addresses.
The fact is that today far from the top processors, in addition to the principle of spatial locality, they also predict an arithmetic progression in the order of memory access. Therefore, you need to randomize memory accesses.
The length of a randomized array should be comparable to the length of the main line in order to get rid of the large granularity of calls, just the length of the array should not be a power of two, because of this there were “overlaps” - which can result in outliers. It is best to set the constant granularity, including, if the granularity is a prime number, then the effects of overlays can be avoided. And the length of the randomized array is a function of the length of the string.
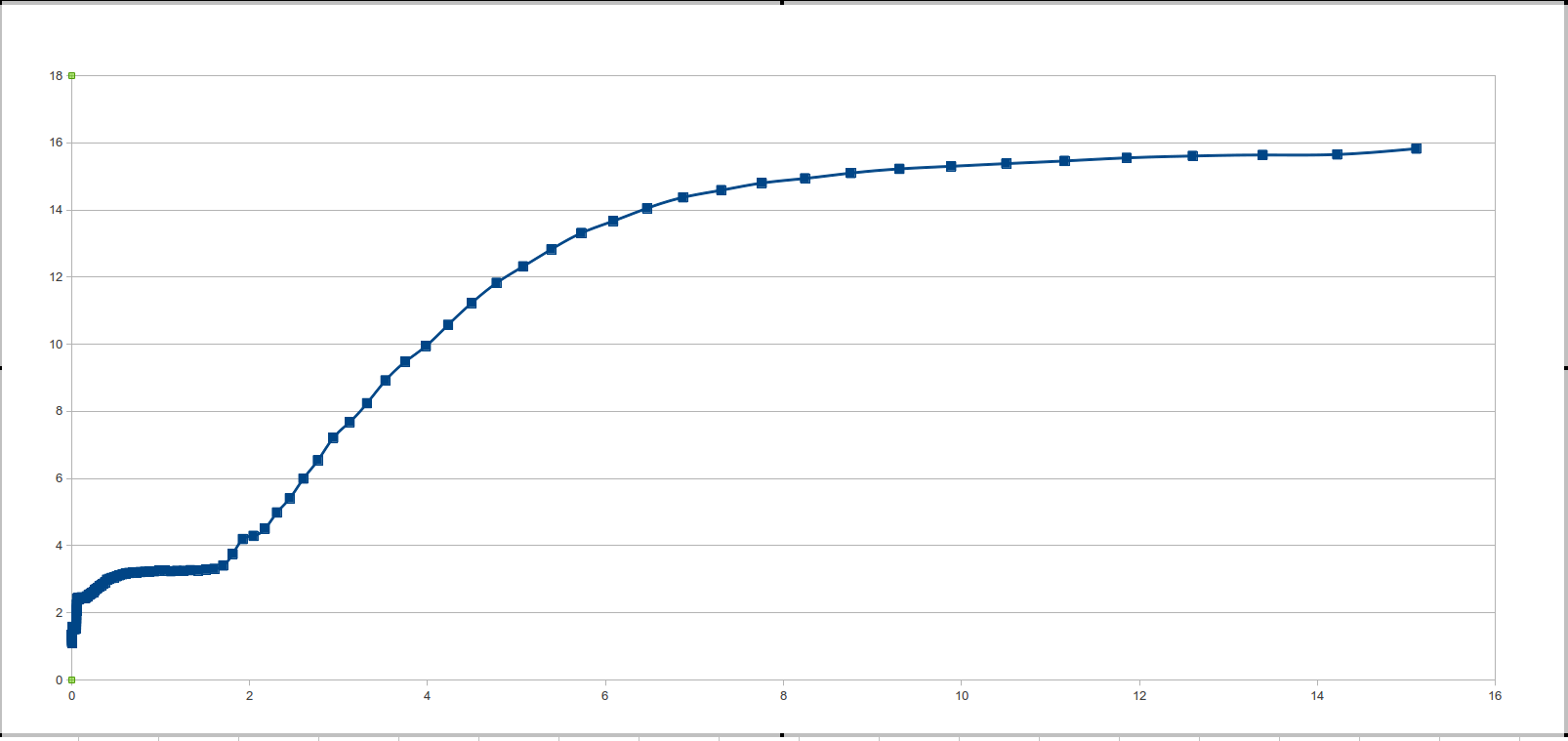
Then we surprised so long-awaited “picture”, which was spoken about at the beginning.
The program is divided into 2 parts - test and data processing. Write a script in 3 lines to run or 2 times to start handles decide for yourself.
Listing file size. With Linux
Listing file size.with Windows
In general, I think everything is clear, but I would like to discuss a few points.
Array A is declared as volatile - this directive guarantees that there will always be references to array A, that is, neither the optimizer nor the compiler will “cut out” them. It is also worthwhile to stipulate that the entire computational load is performed before the time measurement, which allows us to reduce the background effect.
The file is translated into assembler on Ubuntu 12.04 and the gcc 4.6 compiler - the cycles are preserved.
For data processing it is logical to use derivatives. And despite the fact that with an increase in the order of differentiation, the noise increases, the second derivative and its properties will be used. No matter how the second derivative is noisy, we are only interested in the sign of the second derivative.
We find all points where the second derivative is greater than zero (with some error because the second derivative, besides being considered numerically, is very noisy). We set the function of dependence of the sign of the second derivative of the function on the size of the cache. The function takes the value 1 at the points where the sign of the second derivative is greater than zero, and zero if the sign of the second derivative is less than or equal to zero.
Points of "take-off" - the beginning of each step. Also, before processing the data, it is necessary to remove single outliers, which do not change the semantic load of the data, but create noticeable noise.
Listing of the data_pr.c file
CPU / OS / kernel version / compiler / compilation keys - will be listed for each test.
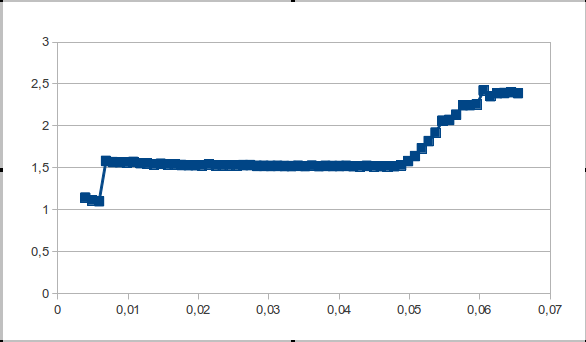
A rake was discovered when processing data on an Intel Xeon 2.4 / L2 server processor = 512 kb / Windows Server 2008
The problem lies in the small number of points falling on the plateau interval, respectively, the jump of the second derivative is imperceptible and is taken as noise.
It is possible to solve this problem using the least squares method, or to run tests in the course of determining the plateau zones.
I would like to hear your suggestions on how to solve this problem.
The speed and frequency of the memory is the main reason why we get “our own piece of free cake” (link). That is why it is important to use memory as efficiently as we can, and even more so as fast as a cache. To optimize the program for a specific computer, it is useful to know the characteristics of the processor's cache memory: the number of levels, size, line length. This is especially important in high-performance code - kernel systems, math libraries.
How to determine the characteristics of the cache automatically? (Naturally, cpuinfo is not considered parsing, though, if only because, ultimately, we would like to get an algorithm that can be easily implemented in other OSes. Convenient, isn't it?) This is what we are going to do now.
')
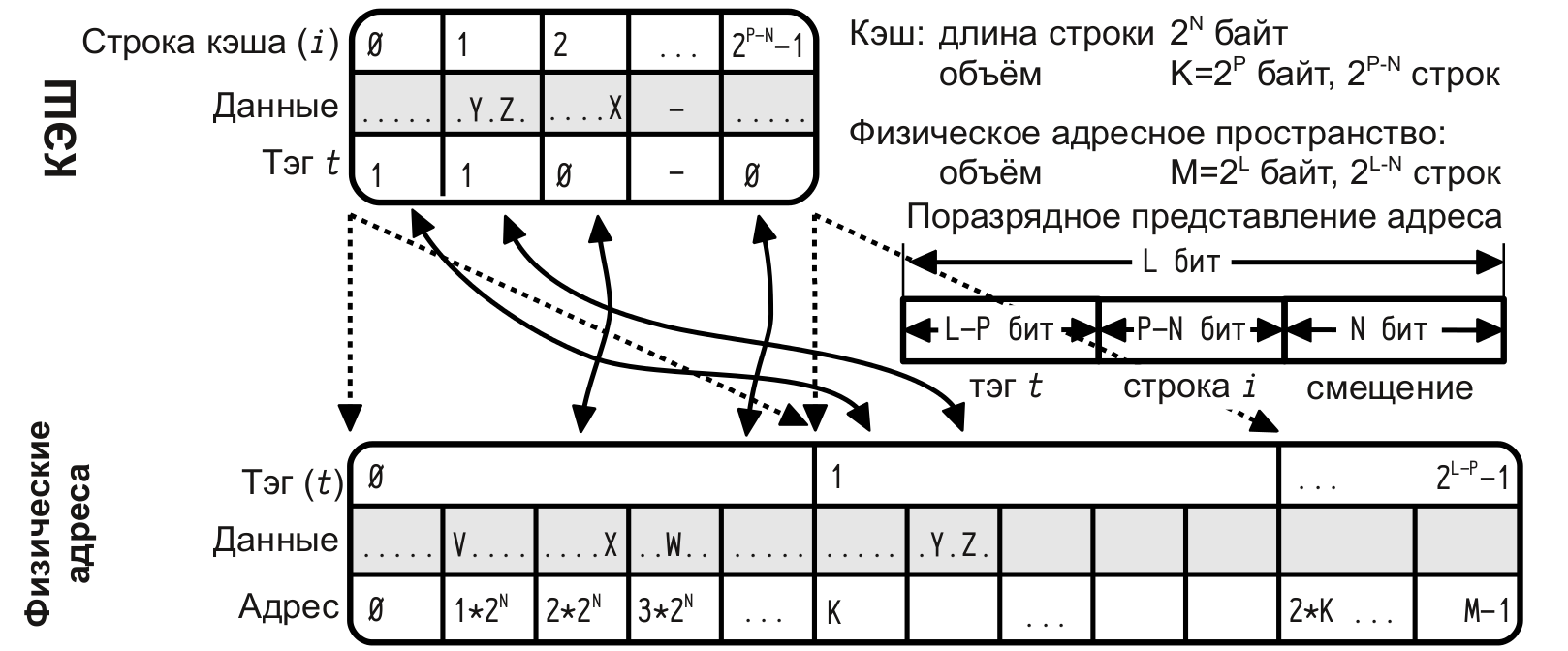
A bit of theory
At the moment, there are three widely used types of cache memory: direct mapping cache, associative cache, and multiple associative cache.
Direct mapping cache
- a given RAM line can be mapped to a single cache line, but many possible RAM lines can be mapped to each cache line.
Associative cache (fully associative cache)
- any line of RAM can be mapped to any cache line.
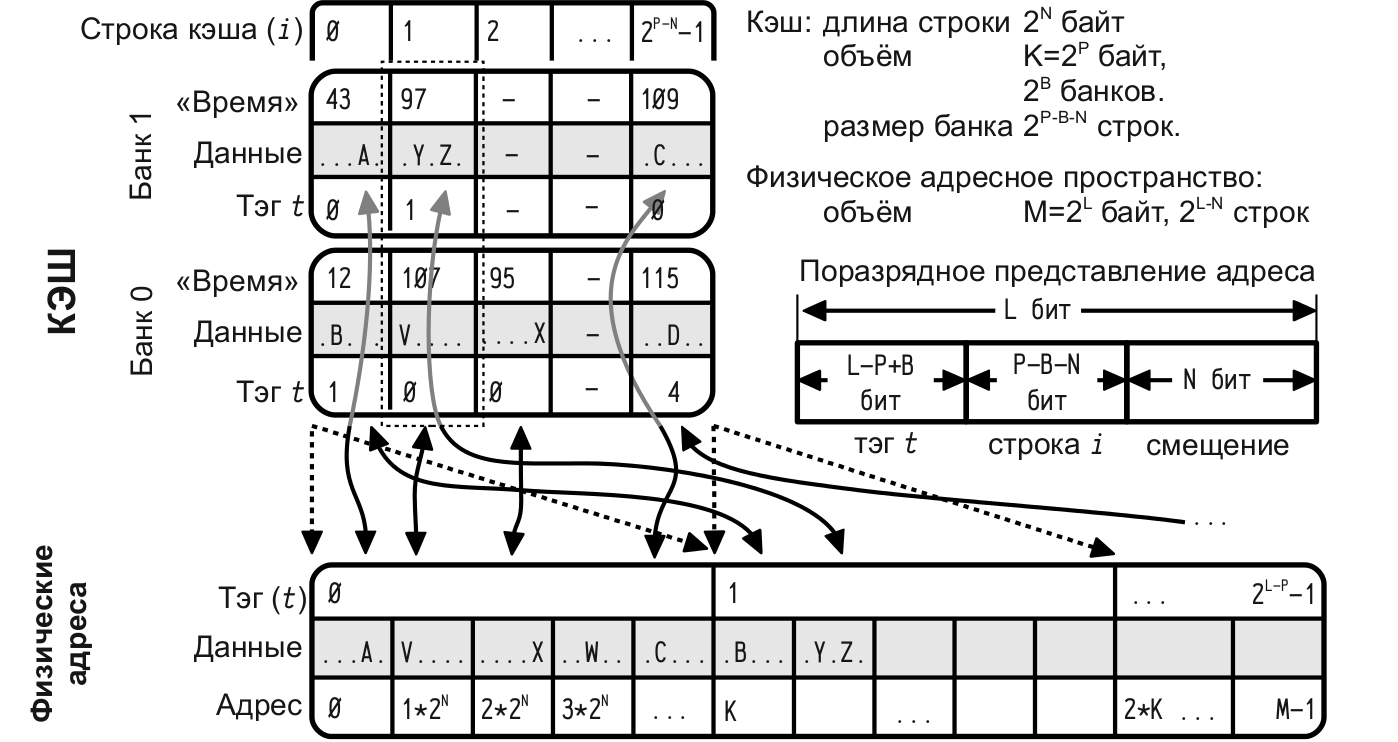
Multiple associative cache
- the cache memory is divided into several “banks”, each of which functions as a cache with direct mapping, so the line of RAM can be mapped not to the only possible cache entry (as it would be in the case of direct mapping), but to one of several banks ; Bank selection is based on LRU or another mechanism for each cache line.
LRU - crowding out the “long unused” line, the memory cache.
Idea
To determine the number of cache levels, you need to consider the order of memory accesses, in which the transition is clearly visible. Different cache levels differ primarily in memory responsiveness. In the case of “cache miss” for the L1 cache, data will be searched in the following memory levels, while if the data size is greater than L1 and less than L2, then the speed of the memory response will be the speed of the L2 response. The previous statement is also true in general cases.
It is clear that you need to pick up a test on which, we will clearly see the cache misses and test it on various data sizes.
Knowing the logic of multiple-associative caches using the LRU algorithm, it is not difficult to come up with an algorithm on which the cache “crashes”, nothing tricky - passing through the line. The criterion of effectiveness will be considered the time of one memory access. Naturally you need to consistently refer to all elements of the line, repeating repeatedly to averaging the result. For example, there may be cases when the string fits in the cache, but for the first pass we load the string from the RAM and therefore we get completely inadequate time.
I want to see something like steps, passing through rows of different lengths. To determine the character of the steps, consider the example of a row pass for the forward and associative cache, the case with the multiply associative cache will be the average between the forward mapping cache and the associative cache.
Associative cache
As soon as the data size exceeds the cache size,
fully associative cache “misses” every time memory is accessed.

Direct cache
Consider different row sizes. - shows the maximum number of misses that the processor will spend to access the elements of the array during the next pass through the line.




As you can see, the memory access time does not increase dramatically, but as the amount of data increases. As soon as the size of the data exceeds the size of the cache, then there will be misses with each memory access.
Therefore, the associative cache will have a vertical step, while the direct cache will gradually increase up to double the cache size. A multiple associative cache would be a middle case, a “bump”, if only because access time cannot be better than a direct one.
If we talk about memory, the fastest is cache, followed by operational, the slowest is swap, we will not talk about it in the future. In turn, different cache levels (as a rule, processors today have 2-3 cache levels) have different memory response rates: the higher the level, the slower the response speed. And therefore, if the line is placed in the first level of the cache (which is by the way fully associative), the response time will be less than that of the line significantly larger than the sizes of the first level cache. Therefore, on the graph of memory response time from the size of the line there will be several plateaus - a plateau * of memory response, and a plateau caused by different levels of cache.
* The function plateau is {i: x, f (xi) - f (xi + 1) <eps: eps → 0}
Let's start the implementation
For implementation we will use C (ANSI C99).
Quickly written code, the usual passage through the rows of different lengths, less than 10mb, performed many times. (We will give small pieces of the program that carry the meaning).
for (i = 0; i < 16; i++) { for (j = 0; j < L_STR; j++) A[j]++; } We look at the chart - and we see one big step. But after all, in theory everything turns out, just wonderful. So you need to understand: why is this happening? And how to fix it?

Obviously, this can happen for two reasons: either there is no memory cache in the processor, or the processor guesses memory references so well. Since the first option is closer to fiction, the reason for all is a good prediction of addresses.
The fact is that today far from the top processors, in addition to the principle of spatial locality, they also predict an arithmetic progression in the order of memory access. Therefore, you need to randomize memory accesses.
The length of a randomized array should be comparable to the length of the main line in order to get rid of the large granularity of calls, just the length of the array should not be a power of two, because of this there were “overlaps” - which can result in outliers. It is best to set the constant granularity, including, if the granularity is a prime number, then the effects of overlays can be avoided. And the length of the randomized array is a function of the length of the string.
for (i = 0; i < j; i++) { for (m = 0; m < L; m++) { for (x = 0; x < M; x++){ v = A[ random[x] + m ]; } } } Then we surprised so long-awaited “picture”, which was spoken about at the beginning.


The program is divided into 2 parts - test and data processing. Write a script in 3 lines to run or 2 times to start handles decide for yourself.
Listing file size. With Linux
#include <stdio.h> #include <stdlib.h> #include <string.h> #include <time.h> #define T char #define MAX_S 0x1000000 #define L 101 volatile TA[MAX_S]; int m_rand[0xFFFFFF]; int main (){ static struct timespec t1, t2; memset ((void*)A, 0, sizeof (A)); srand(time(NULL)); int v, M; register int i, j, k, m, x; for (k = 1024; k < MAX_S;) { M = k / L; printf("%g\t", (k+M*4)/(1024.*1024)); for (i = 0; i < M; i++) m_rand[i] = L * i; for (i = 0; i < M/4; i++) { j = rand() % M; x = rand() % M; m = m_rand[j]; m_rand[j] = m_rand[i]; m_rand[i] = m; } if (k < 100*1024) j = 1024; else if (k < 300*1024) j = 128; else j = 32; clock_gettime (CLOCK_PROCESS_CPUTIME_ID, &t1); for (i = 0; i < j; i++) { for (m = 0; m < L; m++) { for (x = 0; x < M; x++){ v = A[ m_rand[x] + m ]; } } } clock_gettime (CLOCK_PROCESS_CPUTIME_ID, &t2); printf ("%g\n",1000000000. * (((t2.tv_sec + t2.tv_nsec * 1.e-9) - (t1.tv_sec + t1.tv_nsec * 1.e-9)))/(double)(L*M*j)); if (k > 100*1024) k += k/16; else k += 4*1024; } return 0; } Listing file size.with Windows
#include <stdio.h> #include <stdlib.h> #include <string.h> #include <time.h> #include <iostream> #include <Windows.h> using namespace std; #define T char #define MAX_S 0x1000000 #define L 101 volatile TA[MAX_S]; int m_rand[0xFFFFFF]; int main (){ LARGE_INTEGER freq; LARGE_INTEGER time1; LARGE_INTEGER time2; QueryPerformanceFrequency(&freq); memset ((void*)A, 0, sizeof (A)); srand(time(NULL)); int v, M; register int i, j, k, m, x; for (k = 1024; k < MAX_S;) { M = k / L; printf("%g\t", (k+M*4)/(1024.*1024)); for (i = 0; i < M; i++) m_rand[i] = L * i; for (i = 0; i < M/4; i++) { j = rand() % M; x = rand() % M; m = m_rand[j]; m_rand[j] = m_rand[i]; m_rand[i] = m; } if (k < 100*1024) j = 1024; else if (k < 300*1024) j = 128; else j = 32; QueryPerformanceCounter(&time1); for (i = 0; i < j; i++) { for (m = 0; m < L; m++) { for (x = 0; x < M; x++){ v = A[ m_rand[x] + m ]; } } } QueryPerformanceCounter(&time2); time2.QuadPart -= time1.QuadPart; double span = (double) time2.QuadPart / freq.QuadPart; printf ("%g\n",1000000000. * span/(double)(L*M*j)); if (k > 100*1024) k += k/16; else k += 4*1024; } return 0; } In general, I think everything is clear, but I would like to discuss a few points.
Array A is declared as volatile - this directive guarantees that there will always be references to array A, that is, neither the optimizer nor the compiler will “cut out” them. It is also worthwhile to stipulate that the entire computational load is performed before the time measurement, which allows us to reduce the background effect.
The file is translated into assembler on Ubuntu 12.04 and the gcc 4.6 compiler - the cycles are preserved.
Data processing
For data processing it is logical to use derivatives. And despite the fact that with an increase in the order of differentiation, the noise increases, the second derivative and its properties will be used. No matter how the second derivative is noisy, we are only interested in the sign of the second derivative.
We find all points where the second derivative is greater than zero (with some error because the second derivative, besides being considered numerically, is very noisy). We set the function of dependence of the sign of the second derivative of the function on the size of the cache. The function takes the value 1 at the points where the sign of the second derivative is greater than zero, and zero if the sign of the second derivative is less than or equal to zero.
Points of "take-off" - the beginning of each step. Also, before processing the data, it is necessary to remove single outliers, which do not change the semantic load of the data, but create noticeable noise.
Listing of the data_pr.c file
#include <stdio.h> #include <stdlib.h> #include <math.h> double round (double x) { int mul = 100; if (x > 0) return floor(x * mul + .5) / mul; else return ceil(x * mul - .5) / mul; } float size[112], time[112], der_1[112], der_2[112]; int main(){ size[0] = 0; time[0] = 0; der_1[0] = 0; der_2[0] = 0; int i, z = 110; for (i = 1; i < 110; i++) scanf("%g%g", &size[i], &time[i]); for (i = 1; i < z; i++) der_1[i] = (time[i]-time[i-1])/(size[i]-size[i-1]); for (i = 1; i < z; i++) if ((time[i]-time[i-1])/(size[i]-size[i-1]) > 2) der_2[i] = 1; else der_2[i] = 0; //comb for (i = 0; i < z; i++) if (der_2[i] == der_2[i+2] && der_2[i+1] != der_2[i]) der_2[i+1] = der_2[i]; for (i = 0; i < z-4; i++) if (der_2[i] == der_2[i+3] && der_2[i] != der_2[i+1] && der_2[i] != der_2[i+2]) { der_2[i+1] = der_2[i]; der_2[i+2] = der_2[i]; } for (i = 0; i < z-4; i++) if (der_2[i] == der_2[i+4] && der_2[i] != der_2[i+1] && der_2[i] != der_2[i+2] && der_2[i] != der_2[i+3]) { der_2[i+1] = der_2[i]; der_2[i+2] = der_2[i]; der_2[i+3] = der_2[i]; } // int k = 1; for (i = 0; i < z-4; i++){ if (der_2[i] == 1) printf("L%d = %g\tMb\n", k++, size[i]); while (der_2[i] == 1) i++; } return 0; } Tests
CPU / OS / kernel version / compiler / compilation keys - will be listed for each test.
Intel Pentium CPU P6100 @ 2.00GHz / Ubuntu 12.04 / 3.2.0-27-generic / gcc -Wall -O3 size.c -lrt
L1 = 0.05 Mb
L2 = 0.2 Mb
L3 = 2.7 Mb- I will not give all the good tests, let's talk about the "Rake"
Let's talk about "rakes"
A rake was discovered when processing data on an Intel Xeon 2.4 / L2 server processor = 512 kb / Windows Server 2008

The problem lies in the small number of points falling on the plateau interval, respectively, the jump of the second derivative is imperceptible and is taken as noise.
It is possible to solve this problem using the least squares method, or to run tests in the course of determining the plateau zones.
I would like to hear your suggestions on how to solve this problem.
Bibliography
- Makarov A.V. Computer Architecture and Low Level Programming.
- Ulrich Drepper What every programmer should know about memory
Source: https://habr.com/ru/post/148839/
All Articles