Comparison of algorithms for calculating Fibonacci numbers
In the comments to the articles, the Nth Fibonacci number for O (log N) and Another algorithm for calculating Fibonacci numbers indicated the fact that already the 100th Fibonacci number does not fit into 4 bytes, and in "long" arithmetic the speed of multiplication is sharp ask. Moreover, there were suggestions that a primitive addition may turn out to be faster. I decided to compare 2 algorithms — simple addition and an algorithm with a logarithmic number of operations — and wrote a test program in C. I used the GMP library for “long” arithmetic.
Test environment: VirtualBox, Athlon II X3 3.4 GHz, 1GB of RAM, Xubuntu 12.04 64bit, GCC 4.6.3 compiler, O2 optimization
The second algorithm turned out to be much faster. I could not wait for the first algorithm to calculate the billionth Fibonacci number. Algorithm # 2 took 21 seconds to do this.
Results (the time is returned by the clock () function):

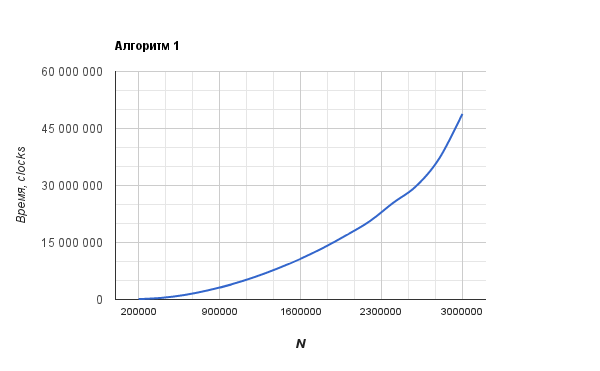
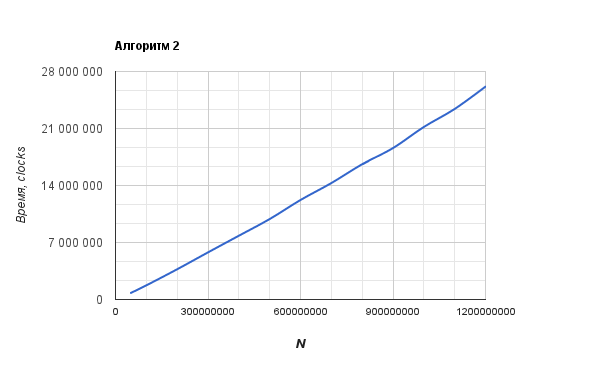
The second graph is very similar to O (N). The graph of the first algorithm is more like O (N ^ 2).
')
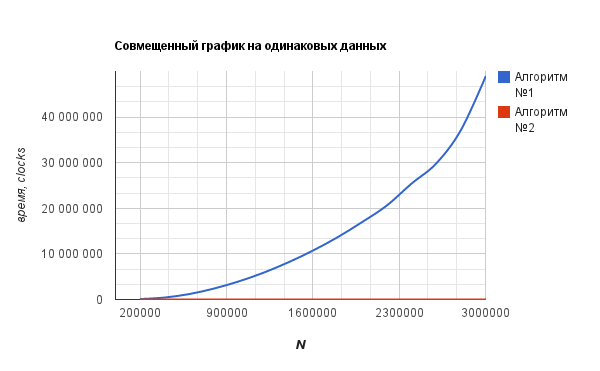
UPD Added a combined schedule. The second algorithm works so fast that its operation time is comparable to the accuracy of the clock () function
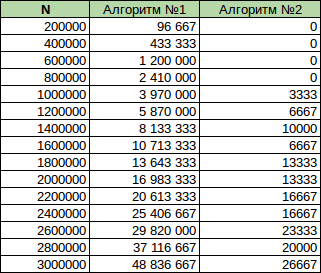
The data on which the graph is built:
Text of the test program
Primitive script to run tests
Input data:
#include <stdio.h> #include <stdlib.h> #include <time.h> #include <gmp.h> void fibonachi1(unsigned int n, mpz_t result); void fibonachi2(unsigned int n, mpz_t result); void dump(unsigned int n); int main(int argc, char* argv[]) { unsigned int n, test_count; clock_t t1, t2; mpz_t result; scanf("%u", &test_count); while (test_count--) { scanf("%u", &n); mpz_init(result); t1 = clock(); fibonachi1(n, result); t2 = clock(); printf("%u\t%u\n", n, (unsigned int)(t2 - t1)); mpz_clear(result); } scanf("%u", &test_count); while (test_count--) { scanf("%u", &n); mpz_init(result); t1 = clock(); fibonachi2(n, result); t2 = clock(); printf("%u\t%u\n", n, (unsigned int)(t2 - t1)); mpz_clear(result); } // dump(10000); return 0; } void fibonachi1(unsigned int n, mpz_t result) { mpz_t last, current; if (n < 2) { mpz_init_set_ui(result, n); } else { mpz_init_set_ui(last, 0); mpz_init_set_ui(current, 1); while (--n > 0) { mpz_swap(last, current); mpz_add(current, current, last); } mpz_swap(current, result); mpz_clear(last); mpz_clear(current); } } void fibonachi2(unsigned int n, mpz_t result) { mpz_t fn, fn1, gn, gn1; if (n < 2) { mpz_init_set_ui(result, n); } else { unsigned mask = 1, m = n; while (m > 1) { m >>= 1; mask <<= 1; } mpz_init_set_ui(fn, 1); mpz_init_set_ui(fn1, 1); mpz_init(gn); mpz_init(gn1); while (mask > 3) { mask >>= 1; mpz_swap(fn, gn); mpz_swap(fn1, gn1); if (n & mask) { mpz_mul(fn, gn1, gn1); mpz_set(fn1, fn); mpz_addmul(fn, gn, gn); mpz_mul(gn, gn, gn1); mpz_add(fn1, fn1, gn); mpz_add(fn1, fn1, gn); } else { mpz_mul(fn, gn, gn1); mpz_add(fn, fn, fn); mpz_mul(gn, gn, gn); mpz_sub(fn, fn, gn); mpz_mul(fn1, gn1, gn1); mpz_add(fn1, fn1, gn); } } if (mask > 1) { mask >>= 1; mpz_swap(fn, gn); mpz_swap(fn1, gn1); if (n & mask) { mpz_mul(fn, gn1, gn1); mpz_addmul(fn, gn, gn); } else { mpz_mul(fn, gn, gn1); mpz_add(fn, fn, fn); mpz_submul(fn, gn, gn); } } mpz_swap(result, fn); mpz_clear(fn1); mpz_clear(gn); mpz_clear(gn1); } } void dump(unsigned int n) { FILE* output; mpz_t result; mpz_init(result); fibonachi1(n, result); output = fopen("alg1.output", "w"); if (output) { mpz_out_str(output, 16, result); fclose(output); } mpz_clear(result); mpz_init(result); fibonachi2(n, result); output = fopen("alg2.output", "w"); if (output) { mpz_out_str(output, 16, result); fclose(output); } mpz_clear(result); } Primitive script to run tests
#!/bin/bash ./main <input.txt >test1.txt ./main <input.txt >test2.txt ./main <input.txt >test3.txt Input data:
15 200000 400000 600000 800000 1000000 1200000 1400000 1600000 1800000 2000000 2200000 2400000 2600000 2800000 3000000 13 50000000 100000000 200000000 300000000 400000000 500000000 600000000 700000000 800000000 900000000 1000000000 1100000000 1200000000 Test environment: VirtualBox, Athlon II X3 3.4 GHz, 1GB of RAM, Xubuntu 12.04 64bit, GCC 4.6.3 compiler, O2 optimization
The second algorithm turned out to be much faster. I could not wait for the first algorithm to calculate the billionth Fibonacci number. Algorithm # 2 took 21 seconds to do this.
Results (the time is returned by the clock () function):

The second graph is very similar to O (N). The graph of the first algorithm is more like O (N ^ 2).


')
UPD Added a combined schedule. The second algorithm works so fast that its operation time is comparable to the accuracy of the clock () function

The data on which the graph is built:

Source: https://habr.com/ru/post/148667/
All Articles