Another algorithm for calculating Fibonacci numbers
Before reading the article , I decided to try to invent my algorithm with the asymptotics O (log N). It took not much time. Below is a description of the idea and an example in C ++.
It is enough just to get this formula:
 where
where 
The formula is proved easily by induction. When m = 0, the formula is true:

Suppose the formula is true for m = p

Prove that the formula is true for m = p + 1:

- obtained the same expression as for the case m = p, i.e. when m = p + 1, the formula remains true
Easy to get through the same numbers:
through the same numbers:
\cdot F_{n-m} + F_{m+1}\cdot F_{n-m-1})
For odd N, m can be chosen so that the equalities hold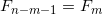 and
and 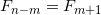 . This number is
. This number is 
After simplification, we obtain the following formulas:
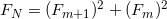


Using the latest formulas you can get a simple recursive algorithm.
')
Recursion is easy enough to leave:
UPD Added an estimate of the asymptotics taking into account the "long" arithmetic
It is enough just to get this formula:
 where
where 
The formula is proved easily by induction. When m = 0, the formula is true:

Suppose the formula is true for m = p

Prove that the formula is true for m = p + 1:

- obtained the same expression as for the case m = p, i.e. when m = p + 1, the formula remains true
Easy to get
 through the same numbers:
through the same numbers:\cdot F_{n-m} + F_{m+1}\cdot F_{n-m-1})
For odd N, m can be chosen so that the equalities hold
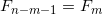 and
and 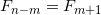 . This number is
. This number is 
After simplification, we obtain the following formulas:
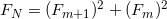


Using the latest formulas you can get a simple recursive algorithm.
')
#include <iostream> using namespace std; void fibonachi_recursive(int n, int& fn, int& fn1) { int gn, gn1; if (n < 2) { fn = n; fn1 = 1; return; } fibonachi_recursive(n / 2, gn, gn1); if (n % 2) { fn = gn1 * gn1 + gn * gn; fn1 = gn1 * gn1 + 2 * gn * gn1; } else { fn = 2 * gn * gn1 - gn * gn; fn1 = gn1 * gn1 + gn * gn; } } int fibonachi(int n) { int fn, fn1; fibonachi_recursive(n, fn, fn1); return fn; } int main() { for (int i = 0; i < 20; i++) cout << fibonachi(i) << " "; return 0; } Recursion is easy enough to leave:
#include <iostream> using namespace std; unsigned fibonachi(unsigned n) { if (n < 2) return n; unsigned mask = 1, m = n; while (m > 1) { m >>= 1; mask <<= 1; } unsigned fn = 1, fn1 = 1, gn, gn1; while (mask > 1) { mask >>= 1; gn = fn; gn1 = fn1; if (n & mask) { fn = gn1 * gn1 + gn * gn; fn1 = gn1 * gn1 + 2 * gn * gn1; } else { fn = 2 * gn * gn1 - gn * gn; fn1 = gn1 * gn1 + gn * gn; } } return fn; } int main() { for (int i = 0; i < 20; i++) cout << fibonachi(i) << " "; return 0; } UPD Added an estimate of the asymptotics taking into account the "long" arithmetic
Source: https://habr.com/ru/post/148531/
All Articles