Nth Fibonacci number for O (log N)
Reading the article on employment with ABBYY , I met in it a reference to the problem:
For convenience, I will move from notation to
to 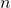 . I will also use the set notation:
. I will also use the set notation:  - non-negative integers,
- non-negative integers,  - positive integers. The fact is that in different mathematical traditions, the set of natural numbers may or may not include 0. Therefore, now in international mathematical texts they prefer to indicate this explicitly.
- positive integers. The fact is that in different mathematical traditions, the set of natural numbers may or may not include 0. Therefore, now in international mathematical texts they prefer to indicate this explicitly.

An identity is presented without proof, but is fairly simply proved by induction.
The matrix on the right is sometimes called the Q-matrix.
Denote:
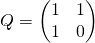
From the identity we get that . Those. to calculate
. Those. to calculate 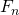 we need to calculate the matrix
we need to calculate the matrix  and take the first element of the first line (numbering from 1).
and take the first element of the first line (numbering from 1).
Since the calculation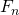 reduced to the construction of a matrix in the degree, then we consider this process in more detail.
reduced to the construction of a matrix in the degree, then we consider this process in more detail.
Suppose we have some matrix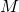 which must be raised to a power
which must be raised to a power  . Suppose also that
. Suppose also that  is a power of two, i.e.
is a power of two, i.e. 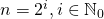 .
.
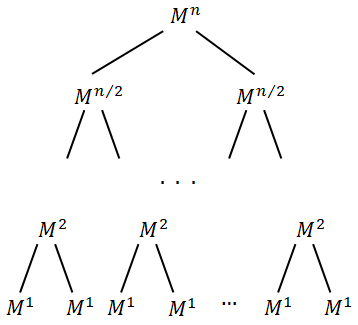
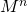 can be represented as a tree:
can be represented as a tree:
Means:
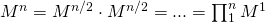 .
.
Accordingly, to calculate the matrix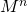 need to calculate the matrix
need to calculate the matrix  and multiply by itself. To calculate
and multiply by itself. To calculate  you need to do the same with
you need to do the same with 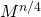 etc.
etc.
Obviously, the height of the tree is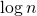 .
.
Estimate the calculation time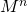 . Matrix
. Matrix 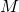 to any extent has a constant size. Therefore, the multiplication of two matrices in any degree can be performed for
to any extent has a constant size. Therefore, the multiplication of two matrices in any degree can be performed for 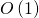 . All such multiplications need to be performed.
. All such multiplications need to be performed.  . Therefore, the complexity of the calculation
. Therefore, the complexity of the calculation 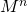 equals
equals 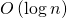 .
.
')
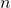 is not a power of two? Any natural number
is not a power of two? Any natural number 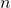 can be decomposed as a sum of numbers that are powers of two, without repetitions (we do this every time we convert a number from a binary number system to a decimal). Those.
can be decomposed as a sum of numbers that are powers of two, without repetitions (we do this every time we convert a number from a binary number system to a decimal). Those.
 ,
,
Where - the set of degrees through which a concrete is expressed
- the set of degrees through which a concrete is expressed 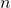 . If you remember that
. If you remember that 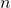 - is the degree of the matrix, then we get:
- is the degree of the matrix, then we get:
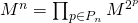 .
.
Although in general the product of matrices is not commutative, i.e. the order of the operands when multiplying is important, but for the so-called. permutation matrices are commutative. Matrix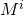 is permutable for
is permutable for 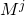 ,
,  . Consequently, we do not have to keep in mind the order of the operands when multiplying, which makes things a little easier.
. Consequently, we do not have to keep in mind the order of the operands when multiplying, which makes things a little easier.
So, the calculation algorithm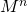 can be represented in the form of the following steps:
can be represented in the form of the following steps:
We estimate the running time of this algorithm.
The first step is performed in time.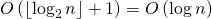 where
where 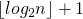 - the number of binary digits in
- the number of binary digits in 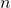 .
.
The second step is performed in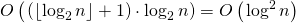 because we need to do no more
because we need to do no more 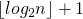 raising the matrix to a power.
raising the matrix to a power.
The third step is performed in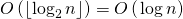 because we need to perform matrix multiplication no more
because we need to perform matrix multiplication no more  time.
time.
 . We know about them that for each of them
. We know about them that for each of them  is a power of two. If you go back to a drawing with a tree, this means that they all lie on certain tiers of the tree and for calculating large ones it is necessary to calculate smaller ones. If we apply the memoization technique and save the calculated matrices on all tiers of the tree, then we can reduce the run time of the second step to
is a power of two. If you go back to a drawing with a tree, this means that they all lie on certain tiers of the tree and for calculating large ones it is necessary to calculate smaller ones. If we apply the memoization technique and save the calculated matrices on all tiers of the tree, then we can reduce the run time of the second step to  and the execution time of the entire algorithm is also up
and the execution time of the entire algorithm is also up  . This is exactly what is required by the condition of the problem.
. This is exactly what is required by the condition of the problem.
It turns out this:
, . :
. :
.
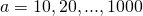 .
. 
 .
. 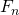 . :
. :
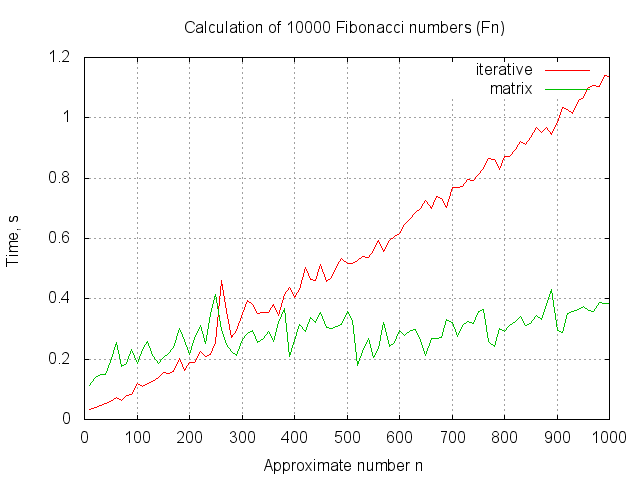
, - (c ,
(c ,  64 ). , , .
64 ). , , .
. gnuplot — .
P.S. , TeX- . , .
quickly - for O (log N) arithmetic operations on numbers - find the N-th Fibonacci numberI thought about it and realized that only decisions that worked during O (N) come to mind. However, a solution was later found.
For convenience, I will move from notation
 to
to 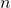 . I will also use the set notation:
. I will also use the set notation:  - non-negative integers,
- non-negative integers,  - positive integers. The fact is that in different mathematical traditions, the set of natural numbers may or may not include 0. Therefore, now in international mathematical texts they prefer to indicate this explicitly.
- positive integers. The fact is that in different mathematical traditions, the set of natural numbers may or may not include 0. Therefore, now in international mathematical texts they prefer to indicate this explicitly.So the solution
Whip [ 1, p. 112 ] gives a matrix identity of the following form:
An identity is presented without proof, but is fairly simply proved by induction.
The matrix on the right is sometimes called the Q-matrix.
Denote:
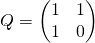
From the identity we get that
 . Those. to calculate
. Those. to calculate 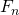 we need to calculate the matrix
we need to calculate the matrix  and take the first element of the first line (numbering from 1).
and take the first element of the first line (numbering from 1).Since the calculation
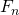 reduced to the construction of a matrix in the degree, then we consider this process in more detail.
reduced to the construction of a matrix in the degree, then we consider this process in more detail.Suppose we have some matrix
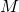 which must be raised to a power
which must be raised to a power 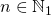 . Suppose also that
. Suppose also that 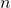 is a power of two, i.e.
is a power of two, i.e. 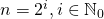 .
.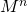 can be represented as a tree:
can be represented as a tree:
Means:
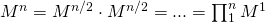 .
.Accordingly, to calculate the matrix
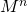 need to calculate the matrix
need to calculate the matrix  and multiply by itself. To calculate
and multiply by itself. To calculate  you need to do the same with
you need to do the same with 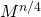 etc.
etc.Obviously, the height of the tree is
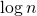 .
.Estimate the calculation time
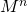 . Matrix
. Matrix 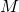 to any extent has a constant size. Therefore, the multiplication of two matrices in any degree can be performed for
to any extent has a constant size. Therefore, the multiplication of two matrices in any degree can be performed for 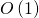 . All such multiplications need to be performed.
. All such multiplications need to be performed.  . Therefore, the complexity of the calculation
. Therefore, the complexity of the calculation 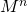 equals
equals 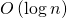 .
.')
And if n is not a power of two?
Now the question arises: what to do if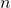 is not a power of two? Any natural number
is not a power of two? Any natural number 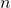 can be decomposed as a sum of numbers that are powers of two, without repetitions (we do this every time we convert a number from a binary number system to a decimal). Those.
can be decomposed as a sum of numbers that are powers of two, without repetitions (we do this every time we convert a number from a binary number system to a decimal). Those. ,
,Where
 - the set of degrees through which a concrete is expressed
- the set of degrees through which a concrete is expressed 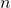 . If you remember that
. If you remember that 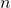 - is the degree of the matrix, then we get:
- is the degree of the matrix, then we get: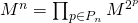 .
.Although in general the product of matrices is not commutative, i.e. the order of the operands when multiplying is important, but for the so-called. permutation matrices are commutative. Matrix
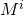 is permutable for
is permutable for 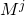 ,
,  . Consequently, we do not have to keep in mind the order of the operands when multiplying, which makes things a little easier.
. Consequently, we do not have to keep in mind the order of the operands when multiplying, which makes things a little easier.So, the calculation algorithm
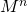 can be represented in the form of the following steps:
can be represented in the form of the following steps:- Decompose
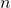 for the sum of powers of two as a set
for the sum of powers of two as a set 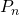 .
. - Calculate all elements of the set
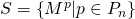 .
. - Calculate
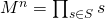 .
.
We estimate the running time of this algorithm.
The first step is performed in time.
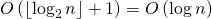 where
where 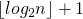 - the number of binary digits in
- the number of binary digits in 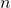 .
.The second step is performed in
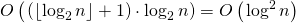 because we need to do no more
because we need to do no more 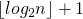 raising the matrix to a power.
raising the matrix to a power.The third step is performed in
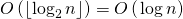 because we need to perform matrix multiplication no more
because we need to perform matrix multiplication no more  time.
time.Optimization
Is it possible to improve the running time of this algorithm? Yes you can. Note that in the second step, in general, the method for calculating the matrices included in the set is not specified. . We know about them that for each of them
. We know about them that for each of them  is a power of two. If you go back to a drawing with a tree, this means that they all lie on certain tiers of the tree and for calculating large ones it is necessary to calculate smaller ones. If we apply the memoization technique and save the calculated matrices on all tiers of the tree, then we can reduce the run time of the second step to
is a power of two. If you go back to a drawing with a tree, this means that they all lie on certain tiers of the tree and for calculating large ones it is necessary to calculate smaller ones. If we apply the memoization technique and save the calculated matrices on all tiers of the tree, then we can reduce the run time of the second step to  and the execution time of the entire algorithm is also up
and the execution time of the entire algorithm is also up  . This is exactly what is required by the condition of the problem.
. This is exactly what is required by the condition of the problem.Code
Let's go to coding. I implemented the Python algorithm for two reasons:- it is expressive enough to replace pseudocode;
- in it is transparent long arithmetic .
It turns out this:
class MatrixFibonacci:
Q = [[1, 1],
[1, 0]]
def __init__(self):
self.__memo = {}
def __multiply_matrices(self, M1, M2):
"""
( 2x2)."""
a11 = M1[0][0]*M2[0][0] + M1[0][1]*M2[1][0]
a12 = M1[0][0]*M2[0][1] + M1[0][1]*M2[1][1]
a21 = M1[1][0]*M2[0][0] + M1[1][1]*M2[1][0]
a22 = M1[1][0]*M2[0][1] + M1[1][1]*M2[1][1]
r = [[a11, a12], [a21, a22]]
return r
def __get_matrix_power(self, M, p):
""" ( p )."""
if p == 1:
return M
if p in self.__memo:
return self.__memo[p]
K = self.__get_matrix_power(M, int(p/2))
R = self.__multiply_matrices(K, K)
self.__memo[p] = R
return R
def get_number(self, n):
""" n-
( n )."""
if n == 0:
return 0
if n == 1:
return 1
# , ,
# .. 62 = 2^5 + 2^4 + 2^3 + 2^2 + 2^0 = 32 + 16 + 8 + 4 + 1.
powers = [int(pow(2, b))
for (b, d) in enumerate(reversed(bin(n-1)[2:])) if d == '1']
# , pythonic: http://pastebin.com/h8cKDkHX
matrices = [self.__get_matrix_power(MatrixFibonacci.Q, p)
for p in powers]
while len(matrices) > 1:
M1 = matrices.pop()
M2 = matrices.pop()
R = self.__multiply_matrices(M1, M2)
matrices.append(R)
return matrices[0][0][0]
mfib = MatrixFibonacci()
for n in range(0, 128):
num = mfib.get_number(n)
print(num)
,
 . :
. :def get_number(self, n):
if n == 0:
return 0
a = 0
b = 1
c = 1
for i in range(n-1):
c = a + b
a = b
b = c
return c
.

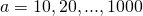 .
. 
MatrixFibonacci IterationFibonacci (, ). 10 000  .
. 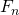 . :
. : n <tab> T1 <tab> T2. .
, -
 (c ,
(c ,  64 ). , , .
64 ). , , .. gnuplot — .
P.S. , TeX- . , .
Source: https://habr.com/ru/post/148336/
All Articles