Computational geometry, or how I became involved in Olympiad programming. Part 2

Introduction

This is the second part of my article devoted to computational geometry. I think this article will be more interesting than the previous one, because the tasks will be a little more complicated.



We begin with the relative position of a point with respect to a straight line, a ray, and a segment.

Task number 1

Determine the relative position of the point and the line: it lies above the line, on the line, under the line.



Decision

It is clear that if the straight line is given by its equation ax + by + c = 0, then there is nothing to solve. It is enough to substitute the coordinates of the point in the equation of the line and check what it is equal to. If more than zero, then the point is in the upper half-plane, if it is equal to zero, then the point is on the straight line and if less than zero, then the point is in the lower half-plane. More interesting is the case when the straight line is given, given by the coordinates of two points we call them P ₁ (x ₁ , y ₁ ), P ₂ (x ₂ , y ₂ ). In this case, you can safely find the coefficients a, b and c and apply the previous argument. But we must first think, we need it? Of course not! As I said oblique works - this is just the pearl of computational geometry. Let's apply it. It is known that the skew product of two vectors is positive, if the rotation from the first vector to the second goes counterclockwise, is zero, if the vectors are collinear and negative, if the rotation goes clockwise. Therefore, it is enough for us to calculate the skew product of the vectors P ₁ P ₂ and P ₁ M and make a conclusion based on its sign.

')

Problem number 2

Determine whether the point belongs to the beam.



Decision

Let's remember what a ray is: a ray is a straight line bounded by a point on the one hand, and on the other hand infinite. That is, the beam is defined by some starting point and any point lying on it. Let the point P ₁ (x ₁ , y ₁ ) be the beginning of the ray, and P ₂ (x ₂ , y ₂ ) be any point belonging to the ray. It is clear that if a point belongs to a ray, then it also belongs to the straight line passing through these points, but not vice versa. Therefore, membership of a straight line is a necessary, but not sufficient condition for belonging to a ray. Therefore, we can’t get away from checking the braid work. For a sufficient condition, you also need to calculate the scalar product of the same vectors. If it is less than zero, then the point does not belong to the ray, but if it is not negative, then the point lies on the ray. Why is that? Let's look at the drawing.







So, for the point M (x, y) to lie on the ray with the initial point P ₁ (x ₁ , y ₁ ), where P ₂ (x ₂ , y ₂ ) lies on the ray, it is necessary and two conditions are sufficient:

1. [P ₁ P ₂ , P ₁ M] = 0 - skew product (point lies on the line)

2. (P ₁ P ₂ , P ₁ M) ≥ 0 - scalar product (point lies on the ray)

Task number 3

Determine whether the point belongs to the segment.



Decision

Let points P ₁ (x ₁ , y ₁ ), P ₂ (x ₂ , y ₂ ) be the ends of a given segment. Again, a necessary condition for a point to belong to a segment is its membership of a straight line passing through P ₁ , P ₂ . Next, we need to determine whether the point lies between the points P ₁ and P ₂ , for this we can use the scalar product of vectors only this time: (MP ₁ , MP ₂ ). If it is less than or equal to zero, then the point lies on the segment, otherwise outside the segment. Why is that? Let's look at the picture.







So, for the point M (x, y) to lie on a segment with the ends P ₁ (x ₁ , y ₁ ), P ₂ (x ₂ , y ₂ ), it is necessary and sufficient that the following conditions be met:

1. [P ₁ P ₂ , P ₁ M] = 0 - skew product (point lies on the line)

2. (MP ₁ , MP ₂ ) ≤ 0 - scalar product (the point lies between P ₁ and P ₂ )

Task number 4

The relative position of two points is relatively straight.



Decision

In this task it is necessary to determine on one or on opposite sides of a straight line there are two points.







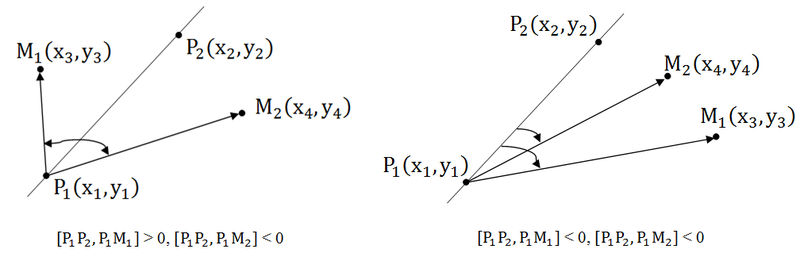
If the points are on opposite sides with respect to a straight line, then skew products have different signs, which means their product is negative. If the points lie on the same side with respect to a straight line, then the signs of skew products coincide, which means that their product is positive.

So:

1. [P ₁ P ₂ , P ₁ M ₁ ] * [P ₁ P ₂ , P ₁ M ₂ ] <0 - the points lie on opposite sides.

2. [P ₁ P ₂ , P ₁ M ₁ ] * [P ₁ P ₂ , P ₁ M ₂ ]> 0 - the points lie on one side.

3. [P ₁ P ₂ , P ₁ M ₁ ] * [P ₁ P ₂ , P ₁ M ₂ ] = 0 - one (or two) of the points lie on the line.



By the way, the problem of determining the presence of an intersection point of a straight line and a segment is solved in the same way. More precisely, this is the same problem: the segment and the line intersect when the ends of the segment are on different sides with respect to a straight line or when the ends of the segment lie on a straight line, that is, you need to require [P ₁ P ₂ , P ₁ M ₁ ] * [P ₁ P ₂ , P ₁ M ₂ ] ≤ 0.

Problem number 5

Determine whether two straight lines intersect.



Decision

We assume that the lines do not coincide. It is clear that straight lines do not intersect, only if they are parallel. Therefore, by finding the condition of parallelism, we can determine whether the lines intersect.

Suppose the straight lines are given by their own equations a ₁ x + b ₁ y + c ₁ = 0 and a ₂ x + b ₂ y + c ₂ = 0. Then the condition of parallelism of the straight lines is that a ₁ b ₂ - a ₂ b ₁ = 0

If the straight lines are given by the points P ₁ (x ₁ , y ₁ ), P ₂ (x ₂ , y ₂ ), M ₁ (x ₃ , y ₃ ), M ₂ (x ₄ , y ₄ ), then the condition for their parallelism is in checks of the skew product of the vectors P ₁ P ₂ and M ₁ M ₂ : if it is zero, then the lines are parallel.







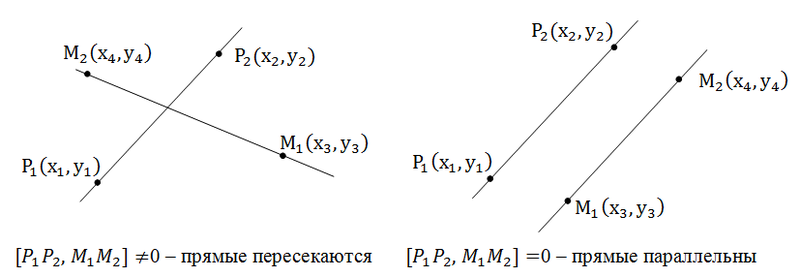
In general, when the straight lines are given by their own equations, we also check the skew product of vectors (-b ₁ , a ₁ ), (-b ₂ , a ₂ ) which are called directing vectors.

Problem number 6

Determine whether two segments intersect.



Decision

I really like this task. The segments intersect when the ends of each segment lie on opposite sides of the other segment. Let's look at the picture:







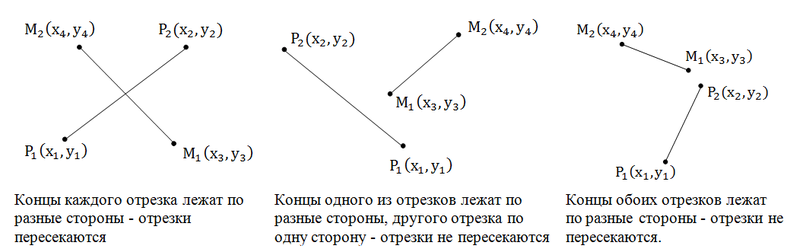
So, we need to check that the ends of each of the segments lie on opposite sides of the relative ends of the other segment. We use the skew product of vectors. Look at the first picture: [P ₁ P ₂ , P ₁ M ₂ ]> 0, [P ₁ P ₂ , P ₁ M ₁ ] <0 => [P ₁ P ₂ , P ₁ M ₂ ] * [P ₁ P ₂ , P ₁ M ₁ ] <0. Similarly

[M ₁ M ₂ , M ₁ P ₁ ] * [M ₁ M ₂ , M ₁ P ₂ ] <0. You probably think why it is not less or equal. And because the following case is possible, in which the vector product is just zero, but the segments do not intersect:







Therefore, we need to make another check, namely, whether at least one end of each segment belongs to the other (the point belongs to the segment). We have already solved this problem.



So, for the segments to have common points, it is necessary and sufficient:

1. The ends of the segments are on different sides relative to another segment.

2. At least one of the ends of one segment belongs to another segment.

Task number 7

The distance from the point to the line.



Decision

Let a straight line be given by two points P ₁ (x ₁ , y ₁ ) and P ₂ (x ₂ , y ₂ ).







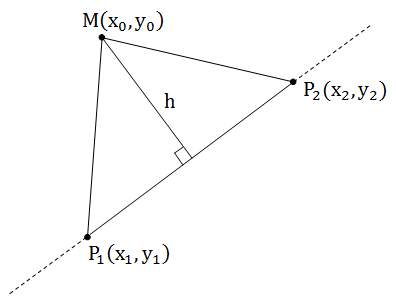
In the previous article, we talked about the fact that the geometrically skew product is an oriented area of ​​a parallelogram, therefore S _{P 1 P 2 M} = 0.5 * [P ₁ P ₂ , P ₁ M]. On the other hand, each schoolchild knows the formula for finding the area of ​​a triangle: half the base of the height.

S _{P 1 P 2 M} = 0.5 * h * P ₁ P ₂ .

Equating these areas, we find



Modulo taken because the first area is oriented.



If the straight line is given by the equation ax + by + c = 0, then the equation of the straight line passing through the point M perpendicular to the given straight line is: a (y - y ₀ ) - b (x - x ₀ ) = 0. Now you can safely solve the system from the obtained equations, find their intersection point and calculate the distance from the source point to the found one: it will be exactly ρ = (ax ₀ + by ₀ + c) / √ (a ² + b ² ).

Problem number 8

The distance from the point to the beam.



Decision

This task differs from the previous one in that it can happen in this case, so the perpendicular from the point does not fall on the ray, but falls on its continuation.







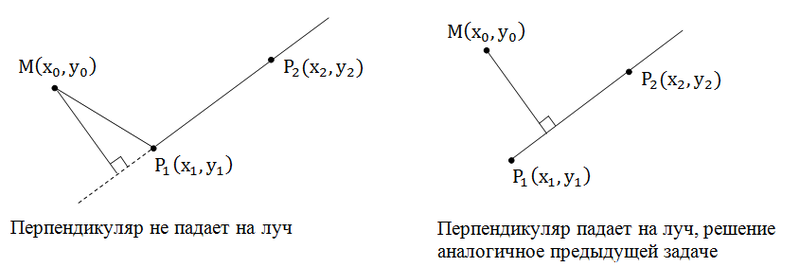
In the case when the perpendicular does not fall on the beam, it is necessary to find the distance from the point to the beginning of the beam - this will be the answer to the problem.



How to determine whether the perpendicular falls on the beam or not? If the perpendicular does not fall on the beam, then the angle MP ₁ P ₂ is blunt or sharp (straight). Therefore, by the sign of the scalar product of vectors, we can determine whether the perpendicular falls on a ray or not:

1. (P ₁ M, P ₁ P ₂ ) <0 perpendicular does not fall on the ray

2. (P ₁ M, P ₁ P ₂ ) ≥ 0 the perpendicular falls on the ray

Problem number 9

The distance from the point to the segment.



Decision

We reason like the previous problem. If the perpendicular does not fall on a segment, then the minimum of the distances from this point to the ends of the segment will be the answer.







To determine whether a perpendicular to a segment falls on, it is necessary, by analogy with the previous task, to use the scalar product of vectors. If the perpendicular does not fall on a segment, then either the angle MP ₁ P ₂ or the angle MP ₂ P ₁ will be obtuse. Therefore, the sign of the scalar products, we can determine whether the perpendicular falls on a segment or not:

If (P ₁ M, P ₁ P ₂ ) <0 or (P ₂ M, P ₂ P ₁ ) <0, then the perpendicular does not fall on the segment.

Problem number 10

Determine the number of points of a line and a circle.



Decision

A line and a circle can have zero, one or two points of intersection. Let's look at the pictures:







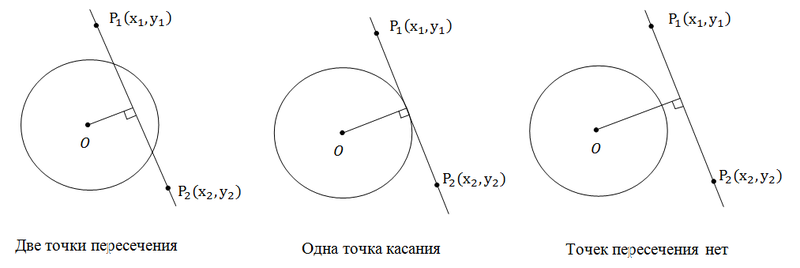
Here from the pictures and so everything is clear. We have two points of intersection if the distance from the center of the circle to the straight line is less than the radius of the circle. One touch point if the distance from the center to the line is equal to the radius. And finally, not a single point of intersection if the distance from the center of the circle to the straight line is greater than the radius of the circle. Since the problem of finding the distance from a point to a straight line has already been solved by us, this problem has also been solved.

Problem number 11

Mutual arrangement of two circles.



Decision

Possible cases of the location of the circles: intersect, touch, do not intersect.







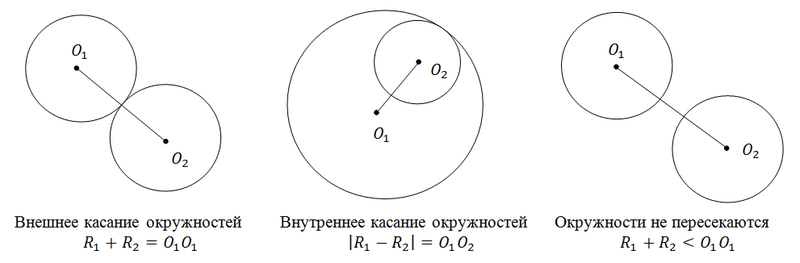
Consider the case when the circles intersect, and find the area of ​​their intersection. I love this task very much, as I spent a fair amount of time on solving it (it was a long time ago - in the first year).







Recall now what a sector and a segment are.





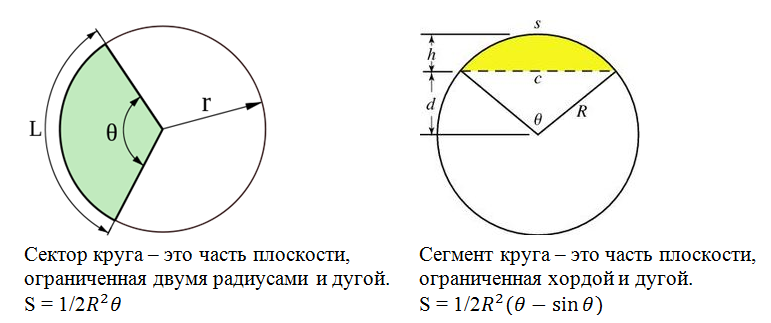
The intersection of circles consists of two segments O ₁ AB and O ₂ AB.







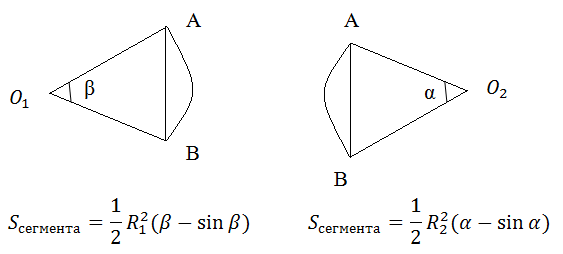
It would seem necessary to add the area of ​​these segments and all. However, things are not so simple. It is also necessary to determine whether these formulas are always correct. It turns out no!



Consider the case when the center of the second circle O ₂ coincides with point C. In this case, d ₂ = 0 and for α we take α = π. In this case, we have a semicircle with an area of ​​1/2 πR ₂ ² .



Now consider the case when the center of the second circle O ₂ is between points O ₁ and C. In this case, we obtain a negative value of d ₂ . The use of a negative d ₂ value leads to a negative α value. In this case, it is necessary for the correct answer to be added to α 2π.

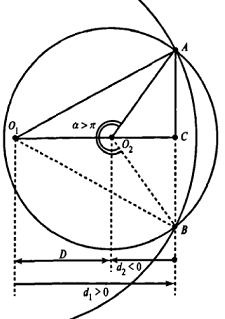
Conclusion

Well that's all. We considered not all, but the most frequently encountered problems of computational geometry concerning the relative position of objects.



Hope you enjoyed it.