The passage of the sapper on the field 9x9 with 32 mines
That's what sometimes harmless entertainment is brought to. 2 months ago, I unexpectedly became interested in playing the sapper. I was especially interested in breaking the record not by time, but by the number of mines on the field. At the level of the game "beginner" is given a field of 9x9 and 10 min. Of course, it was very simple, and I began to increase the number of mines. 12, 15, 20 pieces, it was a simple warm-up. Then passed 25 after a large number of attempts. The game with the 27th mine (every 3rd cell mined) took me several hours. Not stopping there, I put 30 pieces at once. Won after a week and a half, playing an hour a day.
For more than a month I tried to clear 32 mines, and even in the best attempts I had to find about 10 minutes, then it was undermined. And I really wanted to win, and decided that without radical measures I could spend another couple of years. The thought came to write a program to calculate the probability of finding a mine in every cell, at any time of the game.
The main difficulty in the game is where to poke, if the numbers obtained do not make it possible to unambiguously determine the presence or absence of a mine in any cell. But, nevertheless, these probabilities can be very different. If we see that, in a given cell, a mine can theoretically be, but this will be achieved, if several mines are located in strictly defined places, then of course you can click on this cell quite boldly. But personally, I have little idea how these probabilities can be mathematically calculated accurately. Therefore, all these problems had to be shifted to the program. It took 2 hours to write, but finally, having spent a dozen attempts, I won!
Actually the program itself:
')
The algorithm works in the simplest way, which is called “in the forehead”: the user enters data from the minefield, presses a button, then the program places the missing mines randomly in the array, but in such a way that they satisfy the entered data. Filling with mines occurs a sufficiently large number of times, it is calculated how many times a mine has visited each cell, and this number is divided by the number of iterations. That is, the approximate probabilities of the existence of mines in each cell are obtained, and then displayed (as a percentage). (programmers and mathematicians, do not scold too much :)
Data input:
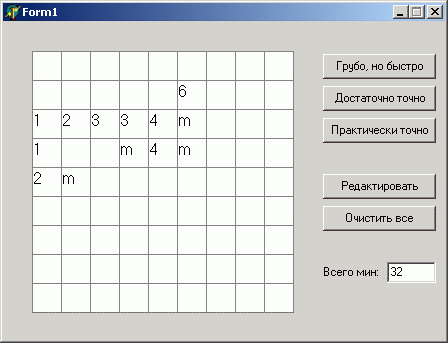
Result:
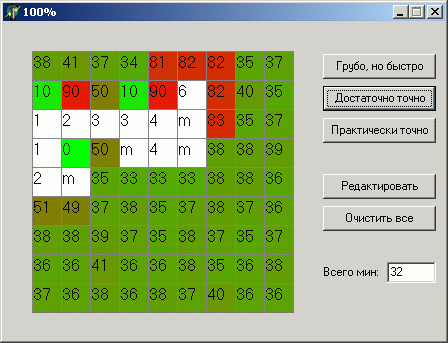
If she is interested in anyone, I will say a few words about the work:
During the game in the sapper you need to enter data on the current state of affairs in the cells. The cell can be empty (if nothing is known about it), a number from 0 to 8, or the letter “m” if the cell is marked with a flag as mined. All 3 buttons on the right calculate probabilities, the difference lies in the different number of iterations (100, 1000, 10000). Therefore, in order to avoid waiting for the calculation too long, I recommend that you first press the first button.
The rest is clear. Download here (200kb). Immediately apologize for the lack of any protection "from a fool."
Everything with the sapper tied. At least for a couple of days.

For more than a month I tried to clear 32 mines, and even in the best attempts I had to find about 10 minutes, then it was undermined. And I really wanted to win, and decided that without radical measures I could spend another couple of years. The thought came to write a program to calculate the probability of finding a mine in every cell, at any time of the game.
The main difficulty in the game is where to poke, if the numbers obtained do not make it possible to unambiguously determine the presence or absence of a mine in any cell. But, nevertheless, these probabilities can be very different. If we see that, in a given cell, a mine can theoretically be, but this will be achieved, if several mines are located in strictly defined places, then of course you can click on this cell quite boldly. But personally, I have little idea how these probabilities can be mathematically calculated accurately. Therefore, all these problems had to be shifted to the program. It took 2 hours to write, but finally, having spent a dozen attempts, I won!
Actually the program itself:
')
The algorithm works in the simplest way, which is called “in the forehead”: the user enters data from the minefield, presses a button, then the program places the missing mines randomly in the array, but in such a way that they satisfy the entered data. Filling with mines occurs a sufficiently large number of times, it is calculated how many times a mine has visited each cell, and this number is divided by the number of iterations. That is, the approximate probabilities of the existence of mines in each cell are obtained, and then displayed (as a percentage). (programmers and mathematicians, do not scold too much :)
Data input:

Result:

If she is interested in anyone, I will say a few words about the work:
During the game in the sapper you need to enter data on the current state of affairs in the cells. The cell can be empty (if nothing is known about it), a number from 0 to 8, or the letter “m” if the cell is marked with a flag as mined. All 3 buttons on the right calculate probabilities, the difference lies in the different number of iterations (100, 1000, 10000). Therefore, in order to avoid waiting for the calculation too long, I recommend that you first press the first button.
The rest is clear. Download here (200kb). Immediately apologize for the lack of any protection "from a fool."
Everything with the sapper tied. At least for a couple of days.

Source: https://habr.com/ru/post/14792/
All Articles