Restore defocused and blurred images. Practice
Not so long ago, I published on Habré the first part of an article on the recovery of defocused and blurred images , where the theoretical part was described. Judging by the comments, this topic caused a lot of interest and I decided to continue this direction and show you what problems appear in the practical implementation of seemingly simple formulas.
In addition to this, I wrote a demo program that implements the basic algorithms for eliminating defocus and blurring. The program is laid out on GitHub along with the sources and distributions.
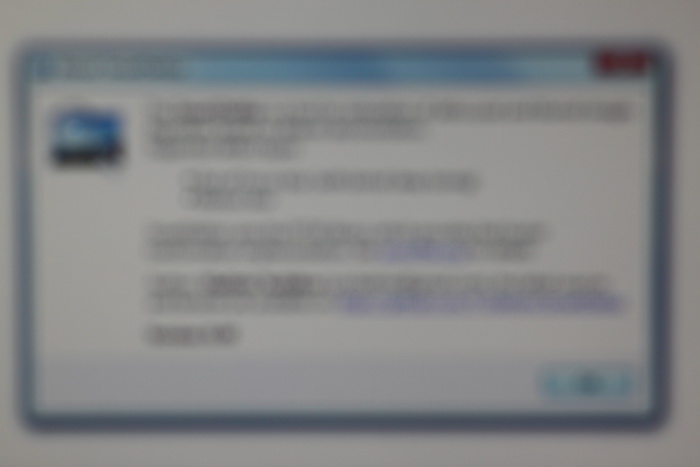
Below is the result of processing a real blurred image (not with synthetic blur). The original image was taken by a Canon 500D camera with an EF 85mm / 1.8 lens. Focus was set manually to get a blur. As you can see, the text is completely unreadable, only the Windows 7 dialog box is guessed.
')
And here is the result of processing:
Almost the entire text reads quite well, although some characteristic distortions appeared.
Under the cat a detailed description of the problems of deconvolution, ways to solve them, as well as many examples and comparisons. Careful, a lot of pictures!
A detailed description of the theory was in the first part, but I will remind you briefly of the main points. In the process of distortion, some spot is obtained from each pixel of the original image in the case of defocusing and a segment for the case of ordinary blurring. All this is superimposed on each other and as a result we get a distorted image - this is called image convolution or convolution. That, according to what law one pixel is smeared and called the distortion function. Other synonyms are PSF (Point spread function, i.e. point distribution function), the core of the distorting operator, kernel, and others.
To restore the original image, we need to somehow reverse the convolution, while not forgetting the noise. But it is not so easy - if you act, as they say, “head on,” you will get a huge system of equations that cannot be solved in a reasonable time.
But to our aid comes the Fourier transform and the convolution theorem, which states that the convolution operation in the spatial domain is equivalent to the usual multiplication in the frequency domain (and the multiplication is element-wise, not matrix). Accordingly, the inverse convolution operation is equivalent to division in the frequency domain. Therefore, the distortion process can be rewritten as follows:
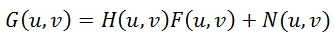(one),
where all elements are Fourier images of the corresponding functions:
G (u, v) is the result of the distortion, i.e. what we see as a result (blurred or defocused image)
H (u, v) is a distorting function, PSF
F (u, v) - the original undistorted image
N (u, v) - additive noise
So, we need to restore the maximum approximation to the original image F (u, v). Simply dividing the right and left parts of H (u, v) does not work, because if there is even a very small noise (and it is always on real images), the term N (u, v) / H (u, v) will dominate, which will lead to the fact that the original image will be completely hidden under the noise.
To solve this problem, more robust methods were developed, one of which is the Wiener filter. He considers the image and noise as random processes and finds such an estimate f ′ for the undistorted image f, so that the standard deviation of these values is minimal:
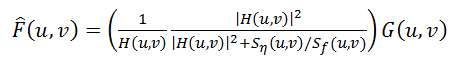(2)
The function S here denotes the energy spectra of the noise and the original image, respectively - since these quantities are rarely known, the fraction S n / S f is replaced by some constant K, which can be approximately characterized as a signal-to-noise ratio.
So, let's take the Wiener filter described as a starting point - in general, there are many other approaches, but they all give roughly the same results. So everything described below will be valid for the rest of the deconvolution methods.
The main task is to obtain an estimate of the point distribution function (PSF). This can be done in several ways:
1. Modeling. It is very difficult and time consuming, because modern lenses consist of a dozen, different different lenses and optical elements, some of which have an aspherical shape, each type of glass has its own unique characteristics of the refraction of rays with a particular wavelength. As a result, the task of correctly calculating the propagation of light in such a complex optical system, taking into account the influence of the diaphragm, the reflections, etc. becomes almost impossible. And its solution, perhaps, is available only to developers of modern lenses.
2. Direct observation. Recall that PSF is what each point in the image turns into. Those. if we form a black background and a single white dot on it, and then take a photo of it with the desired defocus value, we will get the PSF view directly. It seems simple, but there are many nuances and subtleties.
3. Calculation or indirect observation. Let us look at the formula (1) of the distortion process and think about how to get H (u, v)? The solution comes right away - you need to have the original F (u, v) and distorted image G (u, v). Then by dividing the Fourier transform of the distorted image into the Fourier transform of the original image, we get the required PSF.
Before we get into the details, I’ll tell you a little bit of the theory of defocus as applied to optics. The ideal lens has a PSF in the form of a circle, respectively, each point turns into a circle of a certain diameter. By the way, this is a surprise for many people. at first glance it seems that the defocus just blends the whole image. The same explains why the Photoshop Blur of Gauss is not at all like the background image (also called bokeh) that we see in lenses. In fact, these are two different types of blurring - according to Gauss, each point turns into a fuzzy spot (Gauss bell), and defocus turns every point into a circle. Accordingly, different results.
But we don’t have ideal lenses and in reality we get this or that deviation from the ideal circle. This is what forms the unique bokeh pattern of each lens, forcing photographers to spend a lot of money on lenses with beautiful bokeh :) Bokeh can be divided into three types:
- Neutral. This is the maximum approximation to the circle.
- soft. When edges are less bright than center
- Hard. When the edges have greater brightness than the center.
The figure below illustrates this:
Moreover, the type of bokeh - soft or hard depends also on whether it is focus or back focus. Those. the camera is focused in front of or behind the object. For example, if the lens has a soft bokeh pattern in the front focus (when, say, the focus is on the face, and the background is blurred), then in the back focus the bokeh of the same lens will be hard. And vice versa. Only neutral bokeh does not change the type of focus.
But this is not all yet - since some geometrical distortions are inherent in each lens, the PSF view also depends on the position. In the center - close to the circle, on the edges - ellipses and other oblate figures. This is clearly seen in the following photo - note the lower right corner:
And now let's take a closer look at the last two methods for obtaining PSF.
As mentioned above, it is necessary to form a black background and a white dot. But simply printing a single point on the printer is not enough. A much greater difference is needed in the brightness of the black background and the white point, since one point will be blurred in a large circle - respectively, must have greater brightness in order to be visible after blurring.
To do this, I printed Malevich’s black square (yes, the toner went away a lot, but what can't you do for the sake of science!), Put a foil on the other side, because a sheet of paper still shines through well and pierced a small hole with a needle. Then he built a simple design of a 200-watt lamp and a sandwich of black sheet and foil. It looked like this:
Then he turned on the lamp, covered it with a sheet, turned off the general light, and took some photos using two lenses - the whale Canon EF 18-55 and the portrait Canon EF 85mm / 1.8. From the resulting photos, I cut out the PSF and then plotted the profiles.
Here's what happened for the whale lens:
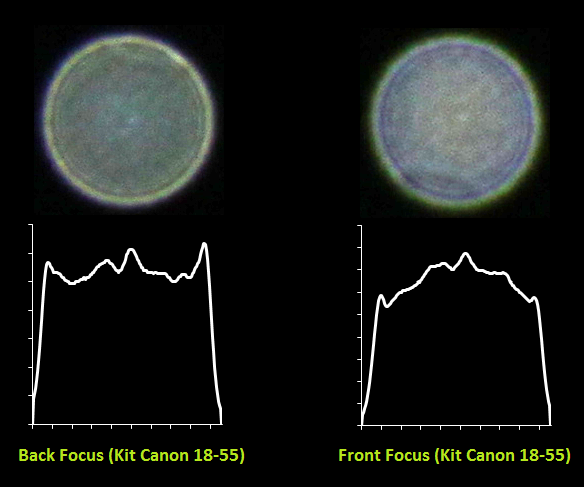
And for the portrait Canon EF 85mm / 1.8:
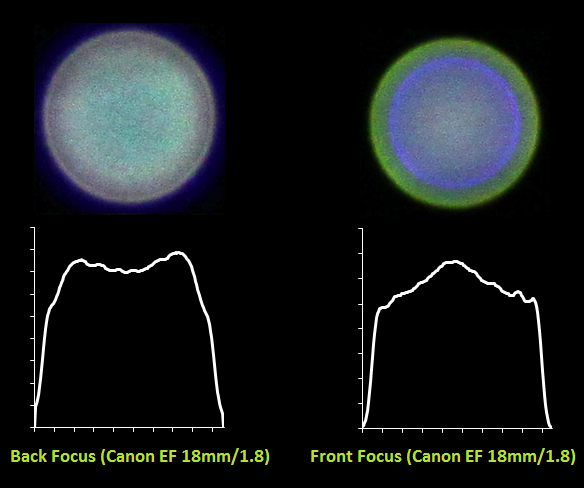
It is clearly seen how the nature of the bokeh changes from soft to soft for the same lens in the case of front and back focus. You can also see what a difficult form PSF has - it is very far from a perfect circle. For the portrait painter, large chromatic aberrations are also visible due to the large aperture of the lens and the small aperture 1.8.
And here is another pair of shots with aperture 14 - it shows how the shape has changed from a circle to a regular hexagon:
The next approach is indirect observation. To do this, as stated above, we need to have the original F (u, v) and the distorted G (u, v) image. How to get them? Very simple - you need to put the camera on a tripod and make one sharp and one blurry shot of the same image. Further, by dividing the Fourier transform of the distorted image into the Fourier transform of the original image, we obtain the Fourier transform of our target PSF. Then, applying the inverse Fourier transform, we obtain the PSF in the direct form.
I took two pictures:
And as a result I received just such a PSF:
Do not pay attention to the horizontal line, this is an artifact after the Fourier transform in the matlab. The result is, let's say, mediocre - a lot of noise and the details of the PSF are not so visible. However, the method has the right to exist.
The described methods can and should be used to build a PSF when restoring blurry images. Because the quality of restoration of the original image directly depends on how close this function is to the real one. If the assumed and real PSFs do not match, numerous artifacts will be observed in the form of “ringing”, halos and a decrease in clarity. In most cases, the shape of a PSF is assumed to be a circle, however, to achieve the maximum degree of recovery, it is recommended to play around with the shape of this function by trying several options from common lenses - as we have seen, the shape of the PSF can vary greatly depending on the aperture, lens and other conditions.
The next problem is that if we directly apply the Wiener filter, then at the edges of the image there will be a kind of “ringing”. Its reason, if explained on the fingers, is as follows: when deconvolution is done for those points that are located at the edges, then the assembly lacks the pixels that are beyond the edges of the image and they are taken either equal to zero or are taken from the opposite side (depends from the implementation of the Wiener filter and the Fourier transform). It looks like this:
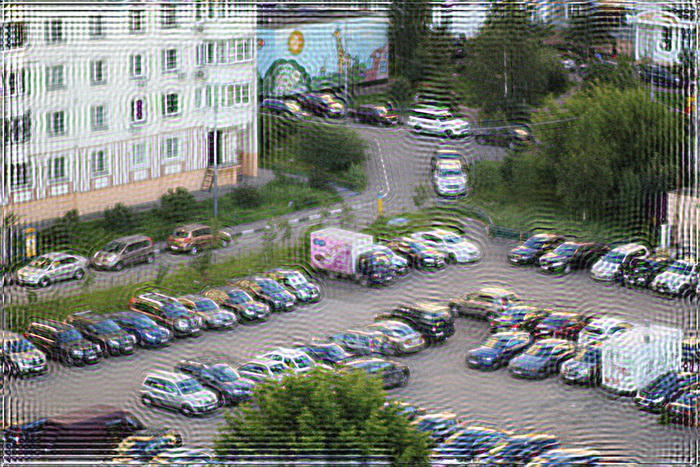
One solution to avoid this is to pre-process the edges of the image. They are blurred with the same PSF. In practice, this is implemented as follows: the input image F (x, y) is taken, blurred with PSF and F '(x, y) is obtained, then the final input image F' '(x, y) is formed by summing F (x, y ) and F '(x, y) using the weight function, which at the edges takes the value 1 (the point is taken entirely from the blurred F' (x, y)), and at a distance equal to or greater than the radius PSF from the edge of the image takes the value 0. The result is this - the ringing at the edges disappeared:
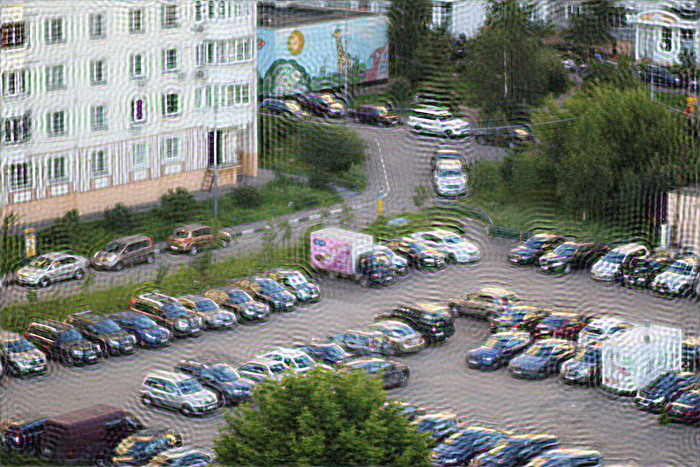
I made a program that demonstrates the recovery of blurred and defocused images. It is written in C ++ using Qt. As the implementation of the Fourier transform, I chose the FFTW library as the fastest of open-source implementations. My program is called SmartDeblur, you can download it at github.com/Y-Vladimir/SmartDeblur , all sources are open under the GPL v3 license.
Screenshot of the main window:
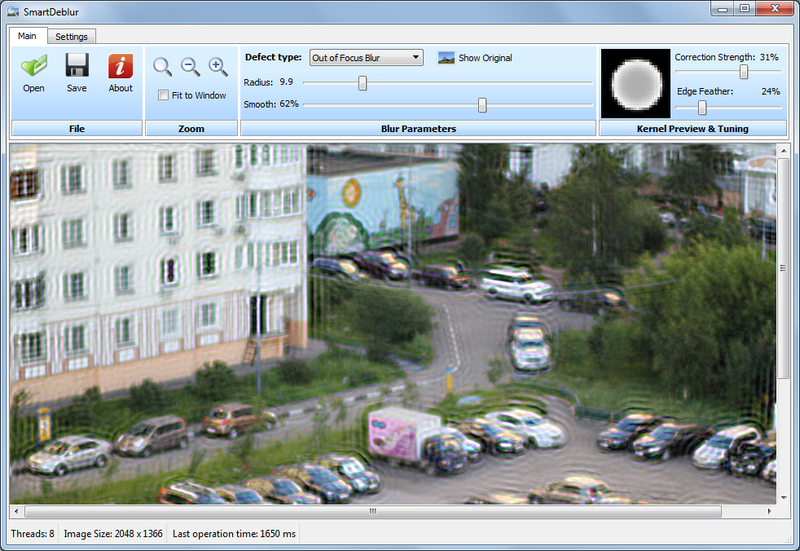
Main functions:
- High speed. Processing an image of 2048 * 1500 pixels in size takes about 300ms in the Preview mode (when the settings sliders are moved) and 1.5 seconds in the fine mode (when the settings sliders are released).
- Selection of parameters in Real-time mode. There is no need to press the Preview buttons, everything is done automatically, you just need to move the sliders of the distortion settings
- All processing goes for the image in full resolution. Those. There is no small preview window and Apply buttons.
- Supports recovery of blurred and defocused images
- Ability to adjust the type of PSF
The main emphasis in the development was on speed. As a result, it turned out to be such that it exceeds commercial counterparts dozens of times. All processing is done in an adult, in a separate thread. For 300 ms, the program manages to generate a new PSF, make 3 Fourier transforms, make a Winer deconvolution, and display the result - all of this for an image of 2048 * 1500 pixels. In the finishing mode, 12 Fourier transforms are made (3 for each channel, plus one for each channel to suppress edge effects) - this takes about 1.5 seconds. All times are for a Core i7 processor.
While the program has a number of bugs and features - for example, with some settings, the image is covered in ripples. It was not possible to find out the exact reason, but presumably the features of the FFTW library.
Well, in general, the development process had to circumvent many hidden problems as in FFTW (for example, images with an odd size of one of the sides, such as 423 * 440.) Are not supported. There were problems with Qt - it turned out that rendering the line with Antialiasing turned on does not work exactly. At some angles, the line jumped to fractions of a pixel, which produced artifacts in the form of strong ripples. To work around this problem, add the lines:
It remains to compare the quality of processing with commercial counterparts.
I chose the 2 most famous programs.
1. Topaz InFocus - www.topazlabs.com/infocus
2. Focus Magic - www.focusmagic.com
For the purity of the experiment, we will take those advertising images that are shown on the official websites - it is so guaranteed that the parameters of those programs are chosen optimal (because I think the developers carefully selected the images and selected the parameters before publishing them on the website).
So, let's go - restoration of lubrication:
Take a cue from Topaz InFocus:
www.topazlabs.com/infocus/_images/licenseplate_compare.jpg
We process with such parameters:
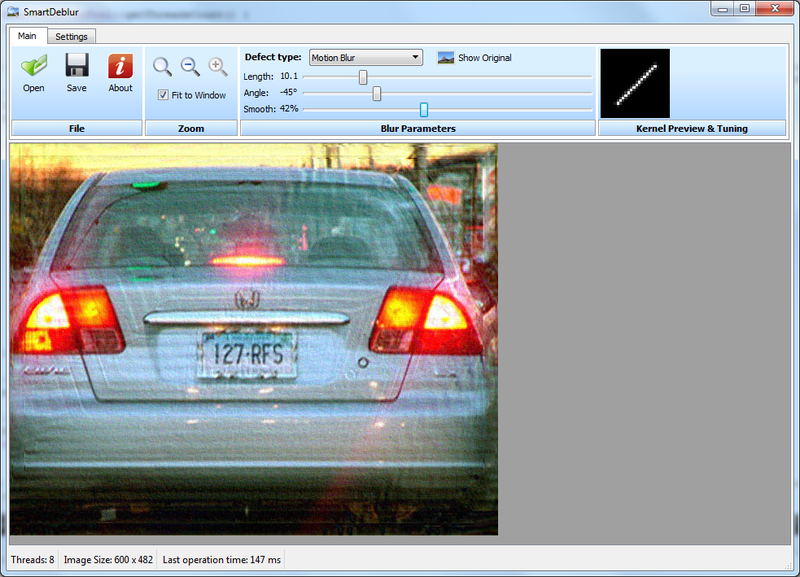
and we get the following result:
Result from Topaz InFocus:
The result is very similar, it says that the basis of Topaz InFocus uses a similar deconvolution algorithm, plus post-processing in the form of smoothing, removing noise and underlining contours.
Examples of strongly defocusing on the site of this program could not be found, and it is not intended for this (the maximum blur radius is only a few pixels).
It is possible to note one more thing - the tilt angle turned out to be exactly 45 degrees, and the length of the blurring is 10 pixels. This suggests that the image is artificially blurred. This fact is also in favor of the fact that the quality of the recovery is very good.
Example number two is defocus recovery. To do this, take an example from the site of Focus Magic: www.focusmagic.com/focusing-examples.htm
We got the following result:
There is no longer so obvious that better.
At this point I would like to finish this article. Although I still wanted to write a lot of other things, I already had a long text. I would be very grateful if you try to download SmartDeblur and test it on real images - unfortunately, I don’t have so many defocused and blurred images, I’ve deleted everything.
And I would be especially grateful if you send me (there is soap in the profile) your feedback and examples of successful / unsuccessful restorations. Well, please report all bugs, comments, suggestions - because The app is still damp and a bit unstable in some places.
PS The source is not very clean in terms of style - there is still a lot of memory leaks, it has not yet been transferred to smart pointers, so after a few images it can stop opening files. But in general it works.
Link to SmartDeblur: github.com/Y-Vladimir/SmartDeblur
UPD: Continuation Link
Vladimir Yuzhikov
In addition to this, I wrote a demo program that implements the basic algorithms for eliminating defocus and blurring. The program is laid out on GitHub along with the sources and distributions.
Below is the result of processing a real blurred image (not with synthetic blur). The original image was taken by a Canon 500D camera with an EF 85mm / 1.8 lens. Focus was set manually to get a blur. As you can see, the text is completely unreadable, only the Windows 7 dialog box is guessed.
')
And here is the result of processing:
Almost the entire text reads quite well, although some characteristic distortions appeared.
Under the cat a detailed description of the problems of deconvolution, ways to solve them, as well as many examples and comparisons. Careful, a lot of pictures!
Recall the theory
A detailed description of the theory was in the first part, but I will remind you briefly of the main points. In the process of distortion, some spot is obtained from each pixel of the original image in the case of defocusing and a segment for the case of ordinary blurring. All this is superimposed on each other and as a result we get a distorted image - this is called image convolution or convolution. That, according to what law one pixel is smeared and called the distortion function. Other synonyms are PSF (Point spread function, i.e. point distribution function), the core of the distorting operator, kernel, and others.
To restore the original image, we need to somehow reverse the convolution, while not forgetting the noise. But it is not so easy - if you act, as they say, “head on,” you will get a huge system of equations that cannot be solved in a reasonable time.
But to our aid comes the Fourier transform and the convolution theorem, which states that the convolution operation in the spatial domain is equivalent to the usual multiplication in the frequency domain (and the multiplication is element-wise, not matrix). Accordingly, the inverse convolution operation is equivalent to division in the frequency domain. Therefore, the distortion process can be rewritten as follows:
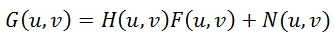(one),where all elements are Fourier images of the corresponding functions:
G (u, v) is the result of the distortion, i.e. what we see as a result (blurred or defocused image)
H (u, v) is a distorting function, PSF
F (u, v) - the original undistorted image
N (u, v) - additive noise
So, we need to restore the maximum approximation to the original image F (u, v). Simply dividing the right and left parts of H (u, v) does not work, because if there is even a very small noise (and it is always on real images), the term N (u, v) / H (u, v) will dominate, which will lead to the fact that the original image will be completely hidden under the noise.
To solve this problem, more robust methods were developed, one of which is the Wiener filter. He considers the image and noise as random processes and finds such an estimate f ′ for the undistorted image f, so that the standard deviation of these values is minimal:
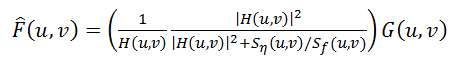(2)The function S here denotes the energy spectra of the noise and the original image, respectively - since these quantities are rarely known, the fraction S n / S f is replaced by some constant K, which can be approximately characterized as a signal-to-noise ratio.
Ways to get PSF
So, let's take the Wiener filter described as a starting point - in general, there are many other approaches, but they all give roughly the same results. So everything described below will be valid for the rest of the deconvolution methods.
The main task is to obtain an estimate of the point distribution function (PSF). This can be done in several ways:
1. Modeling. It is very difficult and time consuming, because modern lenses consist of a dozen, different different lenses and optical elements, some of which have an aspherical shape, each type of glass has its own unique characteristics of the refraction of rays with a particular wavelength. As a result, the task of correctly calculating the propagation of light in such a complex optical system, taking into account the influence of the diaphragm, the reflections, etc. becomes almost impossible. And its solution, perhaps, is available only to developers of modern lenses.
2. Direct observation. Recall that PSF is what each point in the image turns into. Those. if we form a black background and a single white dot on it, and then take a photo of it with the desired defocus value, we will get the PSF view directly. It seems simple, but there are many nuances and subtleties.
3. Calculation or indirect observation. Let us look at the formula (1) of the distortion process and think about how to get H (u, v)? The solution comes right away - you need to have the original F (u, v) and distorted image G (u, v). Then by dividing the Fourier transform of the distorted image into the Fourier transform of the original image, we get the required PSF.
About bokeh
Before we get into the details, I’ll tell you a little bit of the theory of defocus as applied to optics. The ideal lens has a PSF in the form of a circle, respectively, each point turns into a circle of a certain diameter. By the way, this is a surprise for many people. at first glance it seems that the defocus just blends the whole image. The same explains why the Photoshop Blur of Gauss is not at all like the background image (also called bokeh) that we see in lenses. In fact, these are two different types of blurring - according to Gauss, each point turns into a fuzzy spot (Gauss bell), and defocus turns every point into a circle. Accordingly, different results.
But we don’t have ideal lenses and in reality we get this or that deviation from the ideal circle. This is what forms the unique bokeh pattern of each lens, forcing photographers to spend a lot of money on lenses with beautiful bokeh :) Bokeh can be divided into three types:
- Neutral. This is the maximum approximation to the circle.
- soft. When edges are less bright than center
- Hard. When the edges have greater brightness than the center.
The figure below illustrates this:
Moreover, the type of bokeh - soft or hard depends also on whether it is focus or back focus. Those. the camera is focused in front of or behind the object. For example, if the lens has a soft bokeh pattern in the front focus (when, say, the focus is on the face, and the background is blurred), then in the back focus the bokeh of the same lens will be hard. And vice versa. Only neutral bokeh does not change the type of focus.
But this is not all yet - since some geometrical distortions are inherent in each lens, the PSF view also depends on the position. In the center - close to the circle, on the edges - ellipses and other oblate figures. This is clearly seen in the following photo - note the lower right corner:
And now let's take a closer look at the last two methods for obtaining PSF.
PSF - Direct observation
As mentioned above, it is necessary to form a black background and a white dot. But simply printing a single point on the printer is not enough. A much greater difference is needed in the brightness of the black background and the white point, since one point will be blurred in a large circle - respectively, must have greater brightness in order to be visible after blurring.
To do this, I printed Malevich’s black square (yes, the toner went away a lot, but what can't you do for the sake of science!), Put a foil on the other side, because a sheet of paper still shines through well and pierced a small hole with a needle. Then he built a simple design of a 200-watt lamp and a sandwich of black sheet and foil. It looked like this:
Then he turned on the lamp, covered it with a sheet, turned off the general light, and took some photos using two lenses - the whale Canon EF 18-55 and the portrait Canon EF 85mm / 1.8. From the resulting photos, I cut out the PSF and then plotted the profiles.
Here's what happened for the whale lens:
And for the portrait Canon EF 85mm / 1.8:
It is clearly seen how the nature of the bokeh changes from soft to soft for the same lens in the case of front and back focus. You can also see what a difficult form PSF has - it is very far from a perfect circle. For the portrait painter, large chromatic aberrations are also visible due to the large aperture of the lens and the small aperture 1.8.
And here is another pair of shots with aperture 14 - it shows how the shape has changed from a circle to a regular hexagon:
PSF - Computation or Indirect Observation
The next approach is indirect observation. To do this, as stated above, we need to have the original F (u, v) and the distorted G (u, v) image. How to get them? Very simple - you need to put the camera on a tripod and make one sharp and one blurry shot of the same image. Further, by dividing the Fourier transform of the distorted image into the Fourier transform of the original image, we obtain the Fourier transform of our target PSF. Then, applying the inverse Fourier transform, we obtain the PSF in the direct form.
I took two pictures:
And as a result I received just such a PSF:
Do not pay attention to the horizontal line, this is an artifact after the Fourier transform in the matlab. The result is, let's say, mediocre - a lot of noise and the details of the PSF are not so visible. However, the method has the right to exist.
The described methods can and should be used to build a PSF when restoring blurry images. Because the quality of restoration of the original image directly depends on how close this function is to the real one. If the assumed and real PSFs do not match, numerous artifacts will be observed in the form of “ringing”, halos and a decrease in clarity. In most cases, the shape of a PSF is assumed to be a circle, however, to achieve the maximum degree of recovery, it is recommended to play around with the shape of this function by trying several options from common lenses - as we have seen, the shape of the PSF can vary greatly depending on the aperture, lens and other conditions.
Edge effects
The next problem is that if we directly apply the Wiener filter, then at the edges of the image there will be a kind of “ringing”. Its reason, if explained on the fingers, is as follows: when deconvolution is done for those points that are located at the edges, then the assembly lacks the pixels that are beyond the edges of the image and they are taken either equal to zero or are taken from the opposite side (depends from the implementation of the Wiener filter and the Fourier transform). It looks like this:
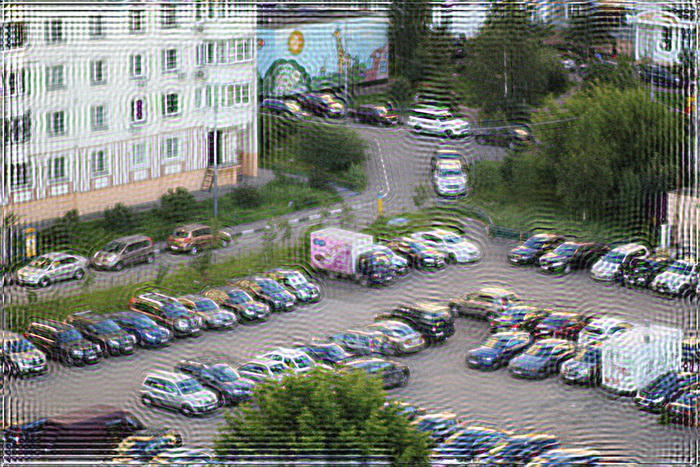
One solution to avoid this is to pre-process the edges of the image. They are blurred with the same PSF. In practice, this is implemented as follows: the input image F (x, y) is taken, blurred with PSF and F '(x, y) is obtained, then the final input image F' '(x, y) is formed by summing F (x, y ) and F '(x, y) using the weight function, which at the edges takes the value 1 (the point is taken entirely from the blurred F' (x, y)), and at a distance equal to or greater than the radius PSF from the edge of the image takes the value 0. The result is this - the ringing at the edges disappeared:
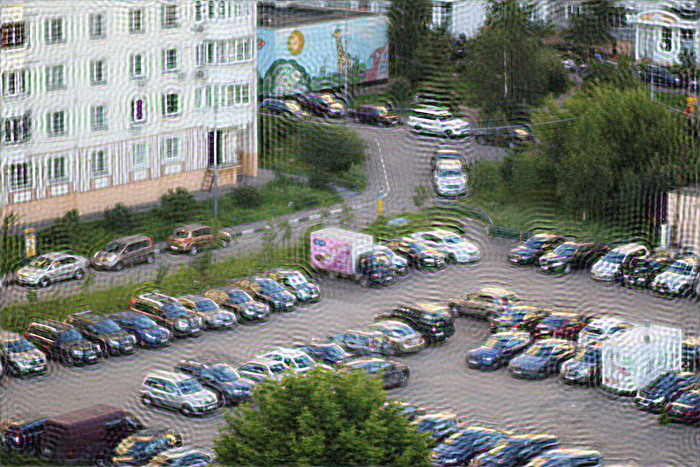
Practical implementation
I made a program that demonstrates the recovery of blurred and defocused images. It is written in C ++ using Qt. As the implementation of the Fourier transform, I chose the FFTW library as the fastest of open-source implementations. My program is called SmartDeblur, you can download it at github.com/Y-Vladimir/SmartDeblur , all sources are open under the GPL v3 license.
Screenshot of the main window:
Main functions:
- High speed. Processing an image of 2048 * 1500 pixels in size takes about 300ms in the Preview mode (when the settings sliders are moved) and 1.5 seconds in the fine mode (when the settings sliders are released).
- Selection of parameters in Real-time mode. There is no need to press the Preview buttons, everything is done automatically, you just need to move the sliders of the distortion settings
- All processing goes for the image in full resolution. Those. There is no small preview window and Apply buttons.
- Supports recovery of blurred and defocused images
- Ability to adjust the type of PSF
The main emphasis in the development was on speed. As a result, it turned out to be such that it exceeds commercial counterparts dozens of times. All processing is done in an adult, in a separate thread. For 300 ms, the program manages to generate a new PSF, make 3 Fourier transforms, make a Winer deconvolution, and display the result - all of this for an image of 2048 * 1500 pixels. In the finishing mode, 12 Fourier transforms are made (3 for each channel, plus one for each channel to suppress edge effects) - this takes about 1.5 seconds. All times are for a Core i7 processor.
While the program has a number of bugs and features - for example, with some settings, the image is covered in ripples. It was not possible to find out the exact reason, but presumably the features of the FFTW library.
Well, in general, the development process had to circumvent many hidden problems as in FFTW (for example, images with an odd size of one of the sides, such as 423 * 440.) Are not supported. There were problems with Qt - it turned out that rendering the line with Antialiasing turned on does not work exactly. At some angles, the line jumped to fractions of a pixel, which produced artifacts in the form of strong ripples. To work around this problem, add the lines:
// Workarround to have high accuracy, otherwise drawLine method has some micro-mistakes in the rendering QPen pen = kernelPainter.pen(); pen.setWidthF(1.01); kernelPainter.setPen(pen); Comparison
It remains to compare the quality of processing with commercial counterparts.
I chose the 2 most famous programs.
1. Topaz InFocus - www.topazlabs.com/infocus
2. Focus Magic - www.focusmagic.com
For the purity of the experiment, we will take those advertising images that are shown on the official websites - it is so guaranteed that the parameters of those programs are chosen optimal (because I think the developers carefully selected the images and selected the parameters before publishing them on the website).
So, let's go - restoration of lubrication:
Take a cue from Topaz InFocus:
www.topazlabs.com/infocus/_images/licenseplate_compare.jpg
We process with such parameters:
and we get the following result:
Result from Topaz InFocus:
The result is very similar, it says that the basis of Topaz InFocus uses a similar deconvolution algorithm, plus post-processing in the form of smoothing, removing noise and underlining contours.
Examples of strongly defocusing on the site of this program could not be found, and it is not intended for this (the maximum blur radius is only a few pixels).
It is possible to note one more thing - the tilt angle turned out to be exactly 45 degrees, and the length of the blurring is 10 pixels. This suggests that the image is artificially blurred. This fact is also in favor of the fact that the quality of the recovery is very good.
Example number two is defocus recovery. To do this, take an example from the site of Focus Magic: www.focusmagic.com/focusing-examples.htm
We got the following result:
 |  |
| SmartDeblur Result | Focus Magic Result |
There is no longer so obvious that better.
Conclusion
At this point I would like to finish this article. Although I still wanted to write a lot of other things, I already had a long text. I would be very grateful if you try to download SmartDeblur and test it on real images - unfortunately, I don’t have so many defocused and blurred images, I’ve deleted everything.
And I would be especially grateful if you send me (there is soap in the profile) your feedback and examples of successful / unsuccessful restorations. Well, please report all bugs, comments, suggestions - because The app is still damp and a bit unstable in some places.
PS The source is not very clean in terms of style - there is still a lot of memory leaks, it has not yet been transferred to smart pointers, so after a few images it can stop opening files. But in general it works.
Link to SmartDeblur: github.com/Y-Vladimir/SmartDeblur
UPD: Continuation Link
--Vladimir Yuzhikov
Source: https://habr.com/ru/post/147828/
All Articles