Computational geometry, or how I became involved in Olympiad programming. Part 1
Hello, dear habravchane! This is my second article, and I would like to talk about computational geometry.
I am a student already 4 courses of the Faculty of Mathematics, and before I started programming, I considered myself a mathematician 100 percent.
At the end of the first course, my computer science teacher, who is involved in Olympiad programming, drew attention to me. They just lacked one math in a team. So slowly they began to teach me to Olympiad programming. Frankly, for me it was very difficult: for a person who learned the word Delphi in the first year. However, my teacher turned out to be a very competent specialist and found a good approach to me. He began to give me mathematical problems, which I first solved purely mathematically, and only then wrote the code (with a sin in half).
')
I really like the approach of my teacher: “deal with this topic, and then tell us, so much so that we all understand.”
So, the first really important task that I was assigned to understand was computational geometry, it was necessary to understand the typical tasks of this section of computer science. And I decided to approach this task with all the responsibility.
I remember how long I suffered with these tasks so that they passed all tests on informatics.mccme. But now I am very glad that I went through all the tests and I know what computational geometry problems are.
“Computational geometry is a branch of computer science that studies algorithms for solving geometric problems. Such tasks arise in computer graphics, design of integrated circuits, technical devices, etc. The initial data in such tasks can be a set of points, a set of segments, polygons, etc. The result can be either an answer to a question or a geometric object. ”
Since the article is quite large, I decided to split it into two parts: the first part is devoted to polygons, the second is the mutual arrangement of various geometric objects.
The segment for which it is indicated which of its ends is considered to be the beginning, and which which is the end, is called a vector. Any point in space can also be considered as a vector. Such a vector is called zero. The beginning and end of the zero vector coincide, and it does not have any particular direction.
The length of a nonzero vector AB is the length of the segment AB. The length of the zero vector is considered to be zero.
Two nonzero vectors are called collinear vectors if they lie on one line or on parallel lines. If two non-zero vectors AB and CD are collinear, and if in this case the rays AB and CD are co-directed, then the vectors AB and CD are called co-directed, and if these rays are not co-directed, then the vectors AB and CD are called oppositely directed. The zero vector is considered to be aligned with any vector.
The scalar product of vectors is a number equal to the product of the lengths of these vectors and the cosine of the angle between them.
(a, b) = | a || b | cos∠ (a, b)
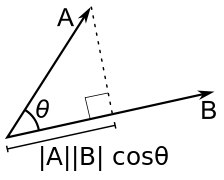
If the vectors are given by their own coordinates a (x 1 , y 1 ), b (x 2 , y 2 ) then the scalar product (a, b) = x 1 x 2 + y 1 y 2 .
Pseudoscalar or oblique product of vectors on a plane is the number
[a, b] = | a || b | sinθ
Where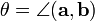
- rotation angle (counterclockwise) from a to b. If at least one of the vectors a and b is zero, then [a, b] = 0 is assumed.
If the vectors are given by their own coordinates a (x 1 , y 1 ), b (x 2 , y 2 ) then the skew product [a, b] = x 1 y 2 - x 2 y 1 .
Geometrically oblique product of vectors is an oriented area of a parallelogram spanned by these vectors.
Oblique product of vectors in computational geometry problems occupies the same honorable place as recursion in combinatorics. This is a kind of gem of computational geometry. Virtually every computational geometry problem has a simpler solution using a skew product instead of a frontal solution.
Let's start with triangles
The task is very simple, namely: from the entered three numbers a, b, c to determine if there is a triangle with such sides.
Decision
It is clear that here it is only necessary to check the triangle inequality: a + b> c, a + c> b, b + c> a. Interestingly, when studying the triangle inequality, did I only have a question: could negative numbers also satisfy these three inequalities? It turns out no! If we add each inequality, we get a> 0, b> 0, c> 0. Therefore, the triangle inequality is a necessary and sufficient condition for the existence of a triangle.
The task is very similar to the previous one with the difference that the triangle is defined not by the sides, but by the coordinates of the vertices.
Decision
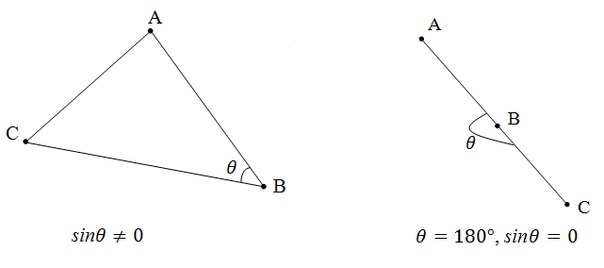
At first glance, the solution seems obvious: calculate the sides of the triangle and reduce the problem to the previous one. However, since the distance between two points A (x 1 , y 1 ), B (x 2 , y 2 ) is calculated by the formula √ (x 1 -x 2 ) 2 + (y 1 -y 2 ) 2, then when you extract the root, you can lose accuracy, which is bad for checking the triangle inequality. It turns out that if a triangle is given by the coordinates of its vertices, then it is not necessary to calculate the lengths of its sides and check the triangle inequality. In this case, a triangle does not exist if and only if these three points lie on one straight line. And this is easily verified through the skew product of vectors. If it is zero, then the vectors are collinear, that is, all three points lie on the same line.
In all the following problems, we assume that a triangle exists, since we have just considered the procedure for checking the existence of a triangle.
The triangle is given by its sides. Determine the type of triangle: obtuse, rectangular or acute.
Decision
Recall what each kind of triangle represents.
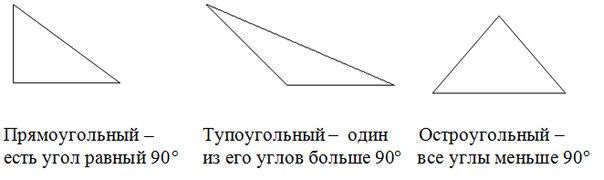
It is known from the course of geometry that a greater angle lies opposite the larger side (we need it). Therefore, if we find out what is the larger angle, then we will understand the type of triangle:
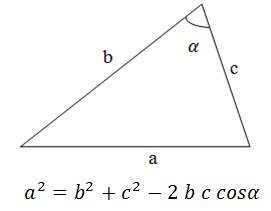
Obviously, if the cosine of the angle is greater than zero, then the angle is less than 90 °, if it is equal to zero, then the angle is equal to 90 °, if it is less than zero, then the angle is greater than 90 °. However, after some thought you can understand that it is not necessary to calculate the cosine of an angle, you only need to take into account its sign:
The task is similar to the previous task, only the triangle is defined not by its sides, but by the coordinates of the vertices.
Decision
Similar to Problem 2, we can say that this problem is completely reduced to the previous problem (the way it is). However, as in the second problem, the solution can be simplified. In general, if a triangle is given by the coordinates of its vertices, then it is always easier to work with it through vectors, rather than calculate sides. Similar to the previous problem, it is necessary to determine which is the largest of the angles of the triangle. The type of angle is easily determined by the sign of the scalar product of the vectors that form it: it is positive for an acute angle, zero for a right angle and negative for an obtuse angle. Therefore, it is necessary to count all three scalar products and multiply them and by the sign of a given number one can judge the type of triangle.
According to the sides of the triangle find its area.
Decision
Obviously the solution is to apply the Heron formula.
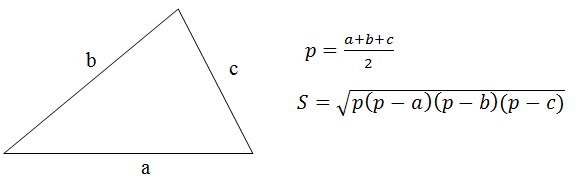
By the way, nobody was interested in the proof of this formula?
Calculate the area of a triangle given by the coordinates of its vertices.
Decision
We will not talk about the solution, which reduces to the previous problem, but try to use the geometric meaning of a skew product. Geometrically oblique product of two vectors determines the oriented area of the parallelogram stretched on these vectors. Since the diagonal of the parallelogram breaks it into two equal-sized triangles, we can find the area of our triangle, as half the area of the parallelogram.
For vectors a (x 1 , y 1 ), b (x 2 , y 2 )
S = (x 1 y 2 - x 2 y 1 ) / 2 - the oriented area of the triangle
Given a point and a triangle given by the coordinates of its vertices. Determine whether the point is inside, on the border or outside of this triangle.
Decision
This problem has two fundamentally different solutions. Let's start with the least attractive.
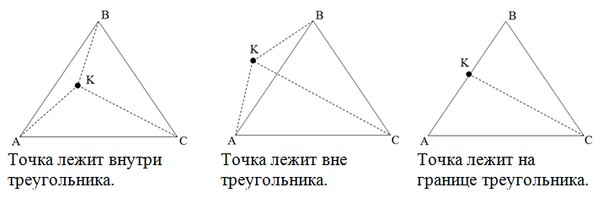
If the sum of the areas of the triangles AKB, AKC, BKC (not oriented, but “ordinary”) is greater than the area of the triangle ABC, the point lies outside the triangle. If the sum of the first three areas is equal to the fourth, then you need to check whether one of the three areas is not equal to zero. If equal, then the point lies on the border of the triangle, otherwise - inside.
To calculate the areas of triangles, of course, it is necessary through the skew product of vectors. This method is not very good. Because it uses a comparison of floating-point numbers, and this in turn can lead to making the wrong decision when comparing. The second method again relies on vectors, it is much more effective in all respects.
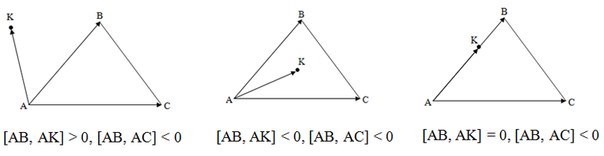
In the first example, the side AB divides the vertex C and the point K along different half-planes, so the point lies outside.
Calculate the area of a polygon given by the coordinates of its vertices.
Decision
By a polygon we mean a simple polygon, that is, without self-intersections. Moreover, it can be either convex or not convex.
This problem can be solved in two ways: by calculating oriented areas of trapezium and triangles.
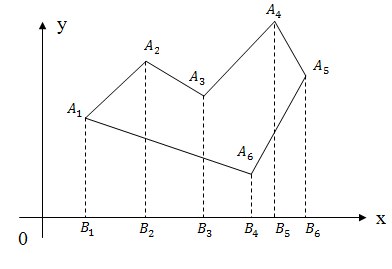
In order to calculate the area of a polygon, you need to split it into a trapezium, as shown in the figure, and then add the oriented areas of the obtained trapeziums to be the oriented area of the original polygon.
S = S A 1 A 2 B 2 B 1 + S A 2 A 3 B 3 B 2 + S A 3 A 4 B 5 B 3 + S A 4 A 5 B 6 B 5 + S A 5 A 6 B 4 B 6 + S A 6 A 1 B 1 B 4
We consider the trapezium areas according to the well-known formula: half-sum of bases for height
S A 1 A 2 B 2 B 1 = 0.5 * (A 1 B 1 + A 2 B 2 ) * (B 2 - B 1 )
Since the resulting area is oriented, it is necessary to calculate its module.
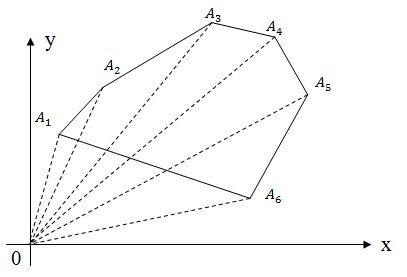
Similarly to the previous method, you can split a polygon not into a trapezoid, but into triangles, as shown in the figure. As a result, adding the oriented areas of these triangles, we again obtain the oriented area of the polygon.
S = S O A 1 A 2 + S O A 2 A 3 + S O A 3 A 4 + S O A 4 A 5 + S O A 5 A 6 + S O A 6 A 1
As you can see, the task of calculating the area of a polygon is quite simple. I don’t know why, but I prefer to solve this problem by splitting into a trapezoid (probably because I solved it in all the Olympiads). Moreover, with the second solution, the areas of the triangles must be calculated through the skew product. On the formula of Gerona must be forgotten !!!
The polygon is given by the coordinates of its vertices in the order of its traversal. It is necessary to check whether the polygon is convex.
Decision
Recall that a polygon is called convex if it lies in the same half-plane with respect to any straight line containing its side.
The problem again reduces to calculating the skew product of vectors, namely, on a convex polygon, the signs of the skew products [A i A i + 1 , A i + 1 A i + 2 ] are either positive or negative. Therefore, if we know the direction of the traversal, then the sign of skew products for a convex polygon is the same: it is non-negative when going counterclockwise and nonpositive when going around clockwise.
The polygon (not necessarily convex) on the plane is given by the coordinates of its vertices. It is required to count the number of points with integer coordinates lying inside it (but not on its boundary).
Decision
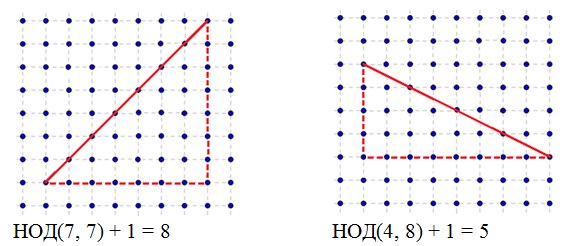
To solve this problem, we consider an auxiliary problem: a segment is given by the coordinates of its ends, which are integers. It is necessary to count the number of integer points lying on the segment. It is clear that if the segment is vertical or horizontal, then it is necessary to subtract the coordinates of the ends and add one. Of interest is the case when the segment is not vertical or horizontal. It turns out that in this case it is necessary to complete the segment to a right-angled triangle and the answer will be a number equal to the greatest common divider of the lengths of the legs of this triangle plus one.
For any polygon with integer coordinates of the vertices, the Peak formula is valid: S = n + m / 2 - 1, where S is the area of the polygon, n is the number of integer points lying strictly inside the polygon, m is the number of integer points lying on the boundary of the polygon. Since the area of the polygon we know how to calculate, then S is known. We can also calculate the number of integer points lying on the boundary of the polygon, therefore, in the Pick formula, there is only one unknown unknown that we can find.
Consider an example:
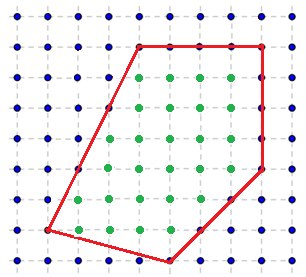
S = 16 + 4 + 4.5 + 6 + 1 + 2 = 33.5
m = 15
n = 33.5 - 7.5 +1 = 27 - points lie strictly inside the polygon
This is how this problem is solved!
That's all! I hope you liked the article, and I will write its second part.
A bit of history
I am a student already 4 courses of the Faculty of Mathematics, and before I started programming, I considered myself a mathematician 100 percent.
At the end of the first course, my computer science teacher, who is involved in Olympiad programming, drew attention to me. They just lacked one math in a team. So slowly they began to teach me to Olympiad programming. Frankly, for me it was very difficult: for a person who learned the word Delphi in the first year. However, my teacher turned out to be a very competent specialist and found a good approach to me. He began to give me mathematical problems, which I first solved purely mathematically, and only then wrote the code (with a sin in half).
')
I really like the approach of my teacher: “deal with this topic, and then tell us, so much so that we all understand.”
So, the first really important task that I was assigned to understand was computational geometry, it was necessary to understand the typical tasks of this section of computer science. And I decided to approach this task with all the responsibility.
I remember how long I suffered with these tasks so that they passed all tests on informatics.mccme. But now I am very glad that I went through all the tests and I know what computational geometry problems are.
Introduction
“Computational geometry is a branch of computer science that studies algorithms for solving geometric problems. Such tasks arise in computer graphics, design of integrated circuits, technical devices, etc. The initial data in such tasks can be a set of points, a set of segments, polygons, etc. The result can be either an answer to a question or a geometric object. ”
Since the article is quite large, I decided to split it into two parts: the first part is devoted to polygons, the second is the mutual arrangement of various geometric objects.
A bit of theory about vectors
The segment for which it is indicated which of its ends is considered to be the beginning, and which which is the end, is called a vector. Any point in space can also be considered as a vector. Such a vector is called zero. The beginning and end of the zero vector coincide, and it does not have any particular direction.
The length of a nonzero vector AB is the length of the segment AB. The length of the zero vector is considered to be zero.
Two nonzero vectors are called collinear vectors if they lie on one line or on parallel lines. If two non-zero vectors AB and CD are collinear, and if in this case the rays AB and CD are co-directed, then the vectors AB and CD are called co-directed, and if these rays are not co-directed, then the vectors AB and CD are called oppositely directed. The zero vector is considered to be aligned with any vector.
Dot product of vectors
The scalar product of vectors is a number equal to the product of the lengths of these vectors and the cosine of the angle between them.
(a, b) = | a || b | cos∠ (a, b)
If the vectors are given by their own coordinates a (x 1 , y 1 ), b (x 2 , y 2 ) then the scalar product (a, b) = x 1 x 2 + y 1 y 2 .
Oblique product of vectors
Pseudoscalar or oblique product of vectors on a plane is the number
[a, b] = | a || b | sinθ
Where
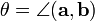- rotation angle (counterclockwise) from a to b. If at least one of the vectors a and b is zero, then [a, b] = 0 is assumed.
If the vectors are given by their own coordinates a (x 1 , y 1 ), b (x 2 , y 2 ) then the skew product [a, b] = x 1 y 2 - x 2 y 1 .
Geometrically oblique product of vectors is an oriented area of a parallelogram spanned by these vectors.
Oblique product of vectors in computational geometry problems occupies the same honorable place as recursion in combinatorics. This is a kind of gem of computational geometry. Virtually every computational geometry problem has a simpler solution using a skew product instead of a frontal solution.
Now let's practice
Let's start with triangles
Task number 1
The task is very simple, namely: from the entered three numbers a, b, c to determine if there is a triangle with such sides.
Decision
It is clear that here it is only necessary to check the triangle inequality: a + b> c, a + c> b, b + c> a. Interestingly, when studying the triangle inequality, did I only have a question: could negative numbers also satisfy these three inequalities? It turns out no! If we add each inequality, we get a> 0, b> 0, c> 0. Therefore, the triangle inequality is a necessary and sufficient condition for the existence of a triangle.
Problem number 2
The task is very similar to the previous one with the difference that the triangle is defined not by the sides, but by the coordinates of the vertices.
Decision
At first glance, the solution seems obvious: calculate the sides of the triangle and reduce the problem to the previous one. However, since the distance between two points A (x 1 , y 1 ), B (x 2 , y 2 ) is calculated by the formula √ (x 1 -x 2 ) 2 + (y 1 -y 2 ) 2, then when you extract the root, you can lose accuracy, which is bad for checking the triangle inequality. It turns out that if a triangle is given by the coordinates of its vertices, then it is not necessary to calculate the lengths of its sides and check the triangle inequality. In this case, a triangle does not exist if and only if these three points lie on one straight line. And this is easily verified through the skew product of vectors. If it is zero, then the vectors are collinear, that is, all three points lie on the same line.
In all the following problems, we assume that a triangle exists, since we have just considered the procedure for checking the existence of a triangle.
Task number 3
The triangle is given by its sides. Determine the type of triangle: obtuse, rectangular or acute.
Decision
Recall what each kind of triangle represents.
It is known from the course of geometry that a greater angle lies opposite the larger side (we need it). Therefore, if we find out what is the larger angle, then we will understand the type of triangle:
- Angle greater than 90 ° - obtuse-angled triangle
- Angle less than 90 ° - acute triangle
- Angle is 90 ° - right triangle
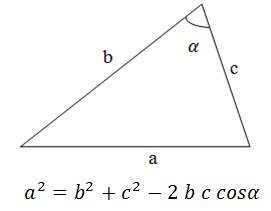
Obviously, if the cosine of the angle is greater than zero, then the angle is less than 90 °, if it is equal to zero, then the angle is equal to 90 °, if it is less than zero, then the angle is greater than 90 °. However, after some thought you can understand that it is not necessary to calculate the cosine of an angle, you only need to take into account its sign:
- If cosα> 0, then a 2 <b 2 + c 2 is an acute triangle
- If cosα = 0, then a 2 = b 2 + c 2 is a right triangle
- If cosα <0, then a 2 > b 2 + c 2 is an obtuse triangle
Task number 4
The task is similar to the previous task, only the triangle is defined not by its sides, but by the coordinates of the vertices.
Decision
Similar to Problem 2, we can say that this problem is completely reduced to the previous problem (the way it is). However, as in the second problem, the solution can be simplified. In general, if a triangle is given by the coordinates of its vertices, then it is always easier to work with it through vectors, rather than calculate sides. Similar to the previous problem, it is necessary to determine which is the largest of the angles of the triangle. The type of angle is easily determined by the sign of the scalar product of the vectors that form it: it is positive for an acute angle, zero for a right angle and negative for an obtuse angle. Therefore, it is necessary to count all three scalar products and multiply them and by the sign of a given number one can judge the type of triangle.
Problem number 5
According to the sides of the triangle find its area.
Decision
Obviously the solution is to apply the Heron formula.
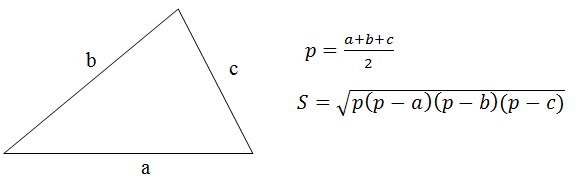
By the way, nobody was interested in the proof of this formula?
Evidence
That's all!
That's all!
Problem number 6
Calculate the area of a triangle given by the coordinates of its vertices.
Decision
We will not talk about the solution, which reduces to the previous problem, but try to use the geometric meaning of a skew product. Geometrically oblique product of two vectors determines the oriented area of the parallelogram stretched on these vectors. Since the diagonal of the parallelogram breaks it into two equal-sized triangles, we can find the area of our triangle, as half the area of the parallelogram.
For vectors a (x 1 , y 1 ), b (x 2 , y 2 )
S = (x 1 y 2 - x 2 y 1 ) / 2 - the oriented area of the triangle
Task number 7
Given a point and a triangle given by the coordinates of its vertices. Determine whether the point is inside, on the border or outside of this triangle.
Decision
This problem has two fundamentally different solutions. Let's start with the least attractive.
Square method
If the sum of the areas of the triangles AKB, AKC, BKC (not oriented, but “ordinary”) is greater than the area of the triangle ABC, the point lies outside the triangle. If the sum of the first three areas is equal to the fourth, then you need to check whether one of the three areas is not equal to zero. If equal, then the point lies on the border of the triangle, otherwise - inside.
To calculate the areas of triangles, of course, it is necessary through the skew product of vectors. This method is not very good. Because it uses a comparison of floating-point numbers, and this in turn can lead to making the wrong decision when comparing. The second method again relies on vectors, it is much more effective in all respects.
Check the half-planes
If at least one of the sides of the triangle divides the opposite vertex and point along different half-planes, then the point lies outside the triangle. Otherwise, if a point belongs to at least one of the lines containing the sides of the triangle, then it is on the border of the triangle. Otherwise, the point lies inside the triangle.
In the first example, the side AB divides the vertex C and the point K along different half-planes, so the point lies outside.
Problem number 8
Calculate the area of a polygon given by the coordinates of its vertices.
Decision
By a polygon we mean a simple polygon, that is, without self-intersections. Moreover, it can be either convex or not convex.
This problem can be solved in two ways: by calculating oriented areas of trapezium and triangles.
Trapezium method
In order to calculate the area of a polygon, you need to split it into a trapezium, as shown in the figure, and then add the oriented areas of the obtained trapeziums to be the oriented area of the original polygon.
S = S A 1 A 2 B 2 B 1 + S A 2 A 3 B 3 B 2 + S A 3 A 4 B 5 B 3 + S A 4 A 5 B 6 B 5 + S A 5 A 6 B 4 B 6 + S A 6 A 1 B 1 B 4
We consider the trapezium areas according to the well-known formula: half-sum of bases for height
S A 1 A 2 B 2 B 1 = 0.5 * (A 1 B 1 + A 2 B 2 ) * (B 2 - B 1 )
Since the resulting area is oriented, it is necessary to calculate its module.
Triangle method
Similarly to the previous method, you can split a polygon not into a trapezoid, but into triangles, as shown in the figure. As a result, adding the oriented areas of these triangles, we again obtain the oriented area of the polygon.
S = S O A 1 A 2 + S O A 2 A 3 + S O A 3 A 4 + S O A 4 A 5 + S O A 5 A 6 + S O A 6 A 1
As you can see, the task of calculating the area of a polygon is quite simple. I don’t know why, but I prefer to solve this problem by splitting into a trapezoid (probably because I solved it in all the Olympiads). Moreover, with the second solution, the areas of the triangles must be calculated through the skew product. On the formula of Gerona must be forgotten !!!
Problem number 9
The polygon is given by the coordinates of its vertices in the order of its traversal. It is necessary to check whether the polygon is convex.
Decision
Recall that a polygon is called convex if it lies in the same half-plane with respect to any straight line containing its side.
The problem again reduces to calculating the skew product of vectors, namely, on a convex polygon, the signs of the skew products [A i A i + 1 , A i + 1 A i + 2 ] are either positive or negative. Therefore, if we know the direction of the traversal, then the sign of skew products for a convex polygon is the same: it is non-negative when going counterclockwise and nonpositive when going around clockwise.
Problem number 10
The polygon (not necessarily convex) on the plane is given by the coordinates of its vertices. It is required to count the number of points with integer coordinates lying inside it (but not on its boundary).
Decision
To solve this problem, we consider an auxiliary problem: a segment is given by the coordinates of its ends, which are integers. It is necessary to count the number of integer points lying on the segment. It is clear that if the segment is vertical or horizontal, then it is necessary to subtract the coordinates of the ends and add one. Of interest is the case when the segment is not vertical or horizontal. It turns out that in this case it is necessary to complete the segment to a right-angled triangle and the answer will be a number equal to the greatest common divider of the lengths of the legs of this triangle plus one.
For any polygon with integer coordinates of the vertices, the Peak formula is valid: S = n + m / 2 - 1, where S is the area of the polygon, n is the number of integer points lying strictly inside the polygon, m is the number of integer points lying on the boundary of the polygon. Since the area of the polygon we know how to calculate, then S is known. We can also calculate the number of integer points lying on the boundary of the polygon, therefore, in the Pick formula, there is only one unknown unknown that we can find.
Consider an example:
S = 16 + 4 + 4.5 + 6 + 1 + 2 = 33.5
m = 15
n = 33.5 - 7.5 +1 = 27 - points lie strictly inside the polygon
This is how this problem is solved!
That's all! I hope you liked the article, and I will write its second part.
Source: https://habr.com/ru/post/147691/
All Articles