Single-line C / C ++. Part 2

Earlier, I already published an article about odnostrochnikikov in C ++ . So in this post I want to mention a few more algorithms, as well as several implementations of the algorithm for the exchange of two numbers (with the calculation of operating time).
I ask all who are interested under the cat;)

1. Check for simplicity

To call this function, write prime(100, int(sqrt(100)));

 bool prime(int n, int div) { return ( div == 1) ? true : (n % div != 0) && (prime(n, div-1)); } 

To avoid this, you can create a wrapper function:

 bool prime(int n) { return ( n == 1 )? 0 : ( prime( n, int(sqrt(n))) ) ; } 

and now it is enough to write prime(100) to call a function

2. Gray code

Gray code is such a numbering system of non-negative numbers, when the codes of two adjacent numbers differ in exactly one bit.

 int codeGrey (int n) { return n ^ (n >> 1); } 

And also finding Gray's reverse code

 int revCodeGrey (int g) { int n; for (n=0; g; n ^=g, g>>=1); return n; } 

Gray codes have several uses in various areas:

• the gray bit code corresponds to the Hamiltonian cycle over the n-dimensional cube
• in solving the problem of the towers of Hanoi
• application in the theory of genetic algorithms

')

3. Calculate the binomial coefficient

The binomial coefficient is the coefficient in the Newton binomial expansion 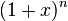by powers of x.

 int binomialCoefficient(int k, int n) { return (n==k || k==0)?1:binomialCoefficient(k-1,n-1)+binomialCoefficient(k,n-1); } 

4. Finding the degree of factorial divisor

Two numbers are given: [n] and [k]. It is required to calculate the degree to which the divisor [k] is included in the number [n].

 int factPow(int n, int k) { return (n)? (n/k + factPow(n/k, k)):0; } 

5. Raising the number [a] to the power [b] modulo [p].

 nt powM(int a, int b, int p) { return b ? (a * powM(a-1, b, p) % p) : 1; } 

Also here you can use the Indian exponentiation algorithm.

 int powM(int a, int b, int p) { return b ? ((b&1?a:1)*powM(a*a, b/2, p) % p) : 1; } 

---

My SWAPa study

So I got the idea to explore a variety of SWAPs, which one is the fastest.
SWAP test will be such a program

  int a=1, b=2; for(int i=0; i<=300000000; i++) { swap(&a, &b); } 

where instead of swap, there will be different algorithms for exchanging two values.

SWAP0

So let's start perhaps from STLivskogo standard algorithm:

 template <class T> void swap0 ( T& a, T& b ) { T c(a); a=b; b=c; } 

his indicators were as follows:

  1,996 sec. 1,986 sec. 1,996 sec. 

SWAP1

The next SWAP will be the so-called XOR SWAP:

 void swap1(int *a, int *b) { *a ^= ( *b ^= ( *a ^= *b )); } 

his indicators were as follows:

  3,603 sec. 3,603 sec. 3,608 sec. 

SWAP2

 void swap2(int *a, int *b) { *a += *b -= *a = *b - *a; } 

her indicators were as follows:

  3.728 sec. 3.723 sec. 3.728 sec. 

SWAP3

 void swap3(int *a, int *b) { *a /= *b = (*a= *a * (*b)) / (*b); } 

her indicators were as follows:

  7.878 sec. 7.862 sec. 7.862 sec. 

SWAP4

 void swap4(int *a, int *b) { *b= *a + *b - (*a = *b); } 

her indicators were as follows:

  2.012 sec. 2.007 sec. 2.012 sec. 

SWAP5

 void swap5(int *a, int *b) { *a=(*b=(*a=*b^*a)^*b)^*a; } 

her indicators were as follows:

  3.198 sec. 3.213 sec. 3.198 sec. 

SWAP6

Well, and the assembler insert for the GCC compiler

 void swap7(int *a, int *b) { asm volatile( "XOR %%EAX, %%EBX; \n\t" "XOR %%EBX, %%EAX; \n\t" "XOR %%EAX, %%EBX; \n\t" :"=a"(*a),"=b"(*b) :"a"(*a),"b"(*b) ); } 

her indicators were as follows:

  2.199 sec. 2.153 sec. 2.167 sec. 

As you can see, our research table is:

1.  SWAP0 - 1.992 sec. 

2.  SWAP4 - 2.010 sec. 

3.  SWAP6 - 2.173 sec. 

4.  SWAP5 - 3.203 sec. 

5.  SWAP1 - 3.604 sec. 

6.  SWAP2 - 3.726 sec. 

7.  SWAP3 - 7.867 sec.