Higgs Boson and Mass Transfer
The roots of the topic here .
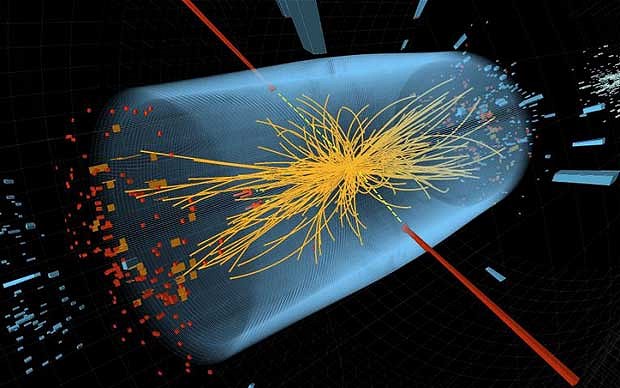
Today at the conference at CERN they officially announced that the ZZ decay channels and the photon-photon give a total confidence of 5 sigma. This means that the threshold between a successful guess and a scientific discovery has been overcome. They definitely discovered the particle. At the same time, the ATLAS experiment is more restrained in its mood.
And this is a great moment to figure out what we know about this particle. Personally, I, as a physics student, are interested in the destruction of the cult of endowing Mass. On this and concentrate. I will try, as far as it is generally possible, to simply and clearly explain the phrase that everyone has heard.
')
To do this, you need to get acquainted with the two cornerstones of theoretical physics - the principle of least action and the Noether theorem .
Many phenomena of modern theory can be explained by a simple construction: giving the Universe a certain symmetry — the Noether theorem is a well-known physical phenomenon. A few examples:
Using the same principle, we can choose a set of symmetries and get a system that corresponds to the modern Standard model. But then we get 4 gauge bosons - photon, W ± and Z, which will have no mass .
At the same time, in the experiment we unambiguously observe 1 massless (photon) and 3 rather heavy particles .
Here it is important to understand that in physics a multitude of phenomena vary greatly in appearance, depending on how we view them - but at the same time, different “representations” still describe the same phenomenon. In quantum physics in general, it is hard to talk about some particles or states - properties strongly depend on the basis on which we decompose them. Recall, at least, kaon oscillations.
We turn specifically to the endowment of mass. The simplest way to understand why we predict massless particles, and we measure massive ones, is in the mechanism of spontaneous symmetry breaking in the system. To understand this mechanism, basic knowledge in classical mechanics is necessary (we study it in the 2nd year at the university) - I cannot count on it, so I will do without formulas as much as I can. Further I refer to Wikipedia.
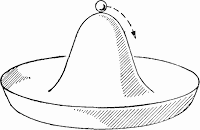
Let us digress and consider the simplest mechanical system: a cylinder of some homogeneous material, placed vertically, on the bases of which we will press. For a while, everything will go well: the cylinder is symmetrical and it gradually becomes shorter under pressure. But at some point the tension inside the cylinder will grow so much that it will become unprofitable for it to condense in length - a condition in which the cylinder is bent to the side becomes preferable and the system tends to it.
At this point, the question arises: which way to bend the cylinder? All directions are the same and the cylinder begins to resemble an antique donkey, who died choosing between two identical haystacks. On the other hand, the system must take some position - and it is not arbitrary, but depends on a much more complex system dynamics. For us, considering the system kinematically, the choice will be random, spontaneous .
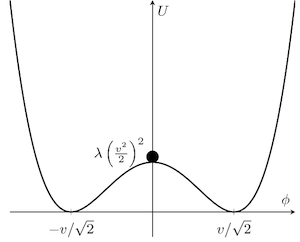
If we look at it in the language of mathematics, we get the following picture:
This is a graph of the energy of the system, and the ball symbolizes its current state. Equivalent to this system will be even simpler: a massless particle in a potential that has the shape exactly as in the image above. But we will look even simpler - on a particle in one dimension on one central section of this graph:
Update: as rightly noted by newpavlov , this is not exactly classical mechanics - here it is more than classical field theory. Therefore, a particle is described not by its coordinate, but by the value of its “density” at points in space. Thank.
Now we will see how it gains mass. Formulas begin. Classical mechanics, 2 course. The first volume of Landau, if you like :) Or else - an article on Wikipedia .
Lagrangian system:

(L is the Lagrange function, phi is the particle density field and depends on the coordinates and time, lambda and v are the parameters of the potential, the derivative is taken from the coordinates and time)
The first term is kinetic, the second one corresponds to the potential in which the particle is located. But everything magically changes if we change the frame of reference. Move 0 of the system to one of the potential minima - we will spontaneously break the symmetry . In fact, we assume that the system has slipped into a certain minimum.

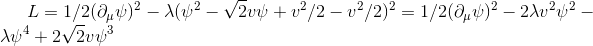
Then it looks like this:

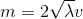
What do we see? Due to the change of variables in the system, a term was singled out, a factor in which we can interpret as the mass of our particle. However, in reality, nothing supernatural happened . We simply changed, if you will, the point of view - moved 3 steps to the left.
In a similar way - only in a much more complicated form - we can see that the recently existing incomplete Standard Model can become not only self-consistent in practice, but also consistent with a much more general theoretical construction.
I note: the Higgs boson can be considered without all of the above. If we forget about symmetries, the Higgs boson becomes just a particle, thanks to the existence of which the experiment converges with theory.
However, this does not detract from the achievement. Today we received confirmation of one of the most successful guesses in theoretical physics.
This is how I imagine the simplest explanation of this interesting focus. Have a good day everyone, do not be fooled by populism!
Special thanks to m0nhawk for help with the pictures.
Today at the conference at CERN they officially announced that the ZZ decay channels and the photon-photon give a total confidence of 5 sigma. This means that the threshold between a successful guess and a scientific discovery has been overcome. They definitely discovered the particle. At the same time, the ATLAS experiment is more restrained in its mood.
And this is a great moment to figure out what we know about this particle. Personally, I, as a physics student, are interested in the destruction of the cult of endowing Mass. On this and concentrate. I will try, as far as it is generally possible, to simply and clearly explain the phrase that everyone has heard.
')

To do this, you need to get acquainted with the two cornerstones of theoretical physics - the principle of least action and the Noether theorem .
Symmetry
Many phenomena of modern theory can be explained by a simple construction: giving the Universe a certain symmetry — the Noether theorem is a well-known physical phenomenon. A few examples:
- homogeneous space - symmetry with respect to translation - the law of conservation of momentum
- time is homogeneous - symmetry with respect to movement in time - the law of conservation of energy (in fact, the same law as with impulse)
- isotropic space - symmetry with respect to rotations - the law of conservation of angular momentum (from this moment you can ride a bicycle)
- a bit more complicated: if we assume that the theory is symmetrical with respect to local gauge transformations - in a few steps you can get light, electricity and all the benefits of civilization
Using the same principle, we can choose a set of symmetries and get a system that corresponds to the modern Standard model. But then we get 4 gauge bosons - photon, W ± and Z, which will have no mass .
At the same time, in the experiment we unambiguously observe 1 massless (photon) and 3 rather heavy particles .
Here it is important to understand that in physics a multitude of phenomena vary greatly in appearance, depending on how we view them - but at the same time, different “representations” still describe the same phenomenon. In quantum physics in general, it is hard to talk about some particles or states - properties strongly depend on the basis on which we decompose them. Recall, at least, kaon oscillations.
Spontaneous symmetry breaking
We turn specifically to the endowment of mass. The simplest way to understand why we predict massless particles, and we measure massive ones, is in the mechanism of spontaneous symmetry breaking in the system. To understand this mechanism, basic knowledge in classical mechanics is necessary (we study it in the 2nd year at the university) - I cannot count on it, so I will do without formulas as much as I can. Further I refer to Wikipedia.
Let us digress and consider the simplest mechanical system: a cylinder of some homogeneous material, placed vertically, on the bases of which we will press. For a while, everything will go well: the cylinder is symmetrical and it gradually becomes shorter under pressure. But at some point the tension inside the cylinder will grow so much that it will become unprofitable for it to condense in length - a condition in which the cylinder is bent to the side becomes preferable and the system tends to it.
At this point, the question arises: which way to bend the cylinder? All directions are the same and the cylinder begins to resemble an antique donkey, who died choosing between two identical haystacks. On the other hand, the system must take some position - and it is not arbitrary, but depends on a much more complex system dynamics. For us, considering the system kinematically, the choice will be random, spontaneous .
If we look at it in the language of mathematics, we get the following picture:

This is a graph of the energy of the system, and the ball symbolizes its current state. Equivalent to this system will be even simpler: a massless particle in a potential that has the shape exactly as in the image above. But we will look even simpler - on a particle in one dimension on one central section of this graph:

Update: as rightly noted by newpavlov , this is not exactly classical mechanics - here it is more than classical field theory. Therefore, a particle is described not by its coordinate, but by the value of its “density” at points in space. Thank.
Now we will see how it gains mass. Formulas begin. Classical mechanics, 2 course. The first volume of Landau, if you like :) Or else - an article on Wikipedia .
Lagrangian system:

(L is the Lagrange function, phi is the particle density field and depends on the coordinates and time, lambda and v are the parameters of the potential, the derivative is taken from the coordinates and time)
The first term is kinetic, the second one corresponds to the potential in which the particle is located. But everything magically changes if we change the frame of reference. Move 0 of the system to one of the potential minima - we will spontaneously break the symmetry . In fact, we assume that the system has slipped into a certain minimum.

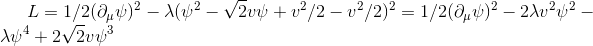
Then it looks like this:

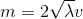
What do we see? Due to the change of variables in the system, a term was singled out, a factor in which we can interpret as the mass of our particle. However, in reality, nothing supernatural happened . We simply changed, if you will, the point of view - moved 3 steps to the left.
findings
In a similar way - only in a much more complicated form - we can see that the recently existing incomplete Standard Model can become not only self-consistent in practice, but also consistent with a much more general theoretical construction.
I note: the Higgs boson can be considered without all of the above. If we forget about symmetries, the Higgs boson becomes just a particle, thanks to the existence of which the experiment converges with theory.
However, this does not detract from the achievement. Today we received confirmation of one of the most successful guesses in theoretical physics.
This is how I imagine the simplest explanation of this interesting focus. Have a good day everyone, do not be fooled by populism!
Special thanks to m0nhawk for help with the pictures.
Source: https://habr.com/ru/post/147100/
All Articles