Tic-tac-toe on Erlang

Introduction

In the article we will try to write a tic-tac-toe game on a 10x10 field, a player (person) with a bot (computer) with the possibility of playing through a browser , the game is considered finished, in the case of one of the 3-oh outcomes:



1) Player won

2) won the computer

3) Draw



Such moments as: installation, verification, configuration of packages are deliberately missed, they repeatedly wrote about the installation of Erlang'a, yet, this program is not built on the principles of OTP. I will accompany all significant moments with schematic pictures.

')

All tests were performed on the hardware:



RAM 4 GB, i5, MAC OS X



The game works correctly in browsers (in the rest the check was not made):

Chrome 19.0.1084.56

FF 13.0.1

Safari 5.1.6 (7534.56.5)

Opera 11.64



Small dictionary:



List - can be viewed as an array;

The symbol is a cross or a toe;

A cell, a point is a cell for a turn, has coordinates (X; Y), where 0 <X and Y <= 10;

Direction - any of 4 variations: horizontal, vertical, first diagonal or second diagonal;

The sequence is a list of 5 coordinates.

Networking

To interact with the user, the program will listen to the port - 8000, and wait for connections, after the client has connected, to initialize the game.



The important point is that the user’s side (browser) must support keep-alive (persistent) connections, the fact is that all player interactions with the program are implemented via ajax get requests, with such an implementation all subsequent ajax get requests will occur through one connection (socket) in unlimited quantity *.



* I didn’t find a specific figure after which browsers forcibly break the connection, but I can definitely say that up to 1000 ajax get requests through one connection, browsers do not initialize the closing of the socket, and in the worst case, one game will need 50 requests to the server.



The code snippet that is responsible for handling clients:

s(Port)-> spawn( fun () -> {ok, Socket} = gen_tcp:listen(Port, [list,{active, false},{packet, http}]), accept_loop(Socket) end). accept_loop(Socket) -> {ok, CSocket} = gen_tcp:accept(Socket), Pid = spawn( fun () -> client_socket() end), gen_tcp:controlling_process(CSocket, Pid), Pid ! {take_socket, Csocket}, % race condition accept_loop(Socket). client_socket() -> Socket = receive {take_socket, S} -> S end, client_loop(Socket, [], []). 

Algorithm

The basic idea of ​​the algorithm is based on the evaluation function, all empty cells are viewed and the efficiency coefficient for this cell is calculated, this is the benefit that we will get if we make a move to this cell, similar actions and for an opponent, what benefit it will receive by making a move to this cell .



Basic formula:



G = M + A * N



M - the benefit of the bot in this cell

N - the benefit of the player in this cell

A is the coefficient of aggressiveness, if the coefficient is increased, the bot will move to a defensive strategy, if reduced, the bot will seek to seize the initiative.



Now let's take a closer look:



Imagine a typical game situation:







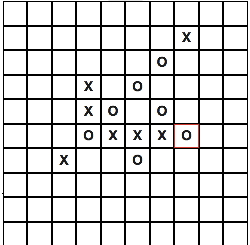
First you need to generate all the nearby coordinates for a single cell, they can be respectively:



3 - if the cell is angular

5 - if the cell is initial or final

8 - for all other options



The code that is responsible for generating is:

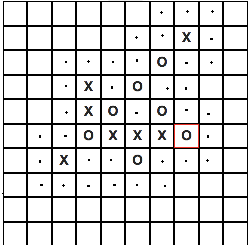
 get_all_empty_points([]) -> []; get_all_empty_points([Head | Tail]) -> lists:usort(get_nearby_points(Head) ++ get_all_empty_points(Tail)). %  get_nearby_points({X,Y}) when X =:= 1 andalso Y =:=1 -> [{X, Y+1}, {X+1, Y+1}, {X+1, Y}]; get_nearby_points({X,Y}) when X =:= 1 andalso Y =:=10 -> [{X+1, Y}, {X+1, Y-1}, {X, Y-1}]; get_nearby_points({X,Y}) when X =:= 10 andalso Y =:=10 -> [{X-1, Y}, {X-1, Y-1}, {X, Y-1}]; get_nearby_points({X,Y}) when X =:= 10 andalso Y =:=1 -> [{X, Y+1}, {X-1, Y+1}, {X-1, Y}]; %   X,Y get_nearby_points({X,Y}) when X =:= 1 -> [{X, Y-1}, {X+1, Y-1}, {X+1, Y}, {X+1, Y+1}, {X, Y+1}]; get_nearby_points({X,Y}) when Y =:= 10 -> [{X+1, Y}, {X+1, Y-1}, {X, Y-1}, {X-1, Y-1}, {X-1, Y}]; get_nearby_points({X,Y}) when X =:= 10 -> [{X, Y-1}, {X-1, Y-1}, {X-1, Y}, {X-1, Y+1}, {X, Y+1}]; get_nearby_points({X,Y}) when Y =:= 1 -> [{X-1, Y}, {X-1, Y+1}, {X, Y+1}, {X+1, Y+1}, {X+1, Y}]; %  get_nearby_points({X,Y}) -> [{X-1, Y+1}, {X, Y+1}, {X+1, Y+1}, {X+1,Y}, {X+1, Y-1}, {X, Y-1}, {X-1, Y-1}, {X-1, Y}]. 

We perform similar actions for each cell to which a move was made, it does not matter if it is a player’s or a bot’s move, after which we delete duplicates and the moves that are already available. As a result, we get a list with the coordinates of all nearby cells, the dots indicate the coordinates that we should get:







Next, you need to calculate directly the benefit of the move to each of the cells. Consider the private option for a single cell and is applicable to all cells in the list that we received earlier.



It is necessary to generate all the continuations (well, or the end, as you like) of the current cell: the horizontal, vertical, first diagonal, second diagonal, in the figure are indicated by dots - the result we should get:







The code that is responsible for generating the coordinates:

 generate_point (horizontal, {X, Y}) -> [{X2,Y} || X2<-lists:seq(X-4, X+4, 1), X2 > 0, X2 < 11]; generate_point (vertical, {X, Y}) -> [{X,Y2} || Y2<-lists:seq(Y-4, Y+4, 1), Y2 > 0, Y2 < 11]; generate_point (fdiagonal, {X, Y}) -> [{X2,Y2} || X2<-lists:seq(X-4, X+4, 1), Y2<-lists:seq(Y-4,Y+4, 1), X2 > 0, Y2 > 0, X2 < 11, Y2 < 11, X2-Y2 == XY]; generate_point (sdiagonal, {X, Y}) -> [{X2,Y2} || X2<-lists:seq(X-4, X+4, 1), Y2<-lists:seq(Y-4,Y+4, 1), X2 > 0, Y2 > 0, X2 < 11, Y2 < 11, X2+Y2 == X+Y]. 

Now consider the private version of the evaluation of effectiveness for the horizontal direction, these actions will be absolutely similar for other areas (verticals, diagonals).



It is necessary to look through all the segments with a length of 5 cells, for this we find the most extreme point, counting 5 cells, and then with a shift of one cell we look through 4 more segments, you can clearly see in the picture:







The picture above shows a simple example just for clarity, unrelated to the game situation. When we look at a segment of 5 cells, we must follow some instructions for each of the 5 sequences:



1) If the sequence is interrupted by the opposite symbol, the weight of this sequence is equal to zero.

2) If there is a cell with the current symbol in the sequence, the counter value is incremented by 1, and we move to the next position.

3) If an empty cell is present in the sequence, we skip it and go to the next position, without increasing the counter value.

4) If a sequence of 5 current symbols is assembled, a sequence is equal to a large weight, if a sequence has collected a bot - its weight is equal to 10,000, if the sequence is collected by a player - its weight is equal to 1,000, the fact is that the bot must rate its victory higher than your defense in this situation.

5) If the sequence length is 1, we equate it to 0, this is only our imaginary move.



The formula for the evaluation function:



L

Gh = ∑ K ^C

i = 1



L is the total number of nonzero sequences

K - coefficient, in our case - 3

C - the total number of characters in the sequence, paragraph 2.



Similarly, we calculate for all directions: verticals, for 2 diagonals, then we summarize all the values, this is a numerical benefit:



M, N = Ghor + Gver + Gfdiag + Gsdiag



The code that is responsible for calculating the efficiency:

 calculate_point_gravity(_, _, [], _) -> []; calculate_point_gravity(MovesX , MovesY, [Move | Rest], Aggress) -> PGravityX = calculate(generate_point(horizontal, Move), MovesX ++ [Move], MovesY, [], Move, 1000) + calculate(generate_point(vertical, Move), MovesX ++ [Move], MovesY, [], Move, 1000) + calculate(generate_point(fdiagonal, Move), MovesX ++ [Move], MovesY, [], Move, 1000) + calculate(generate_point(sdiagonal, Move), MovesX ++ [Move], MovesY, [], Move, 1000), PGravityY = calculate(generate_point(horizontal, Move), MovesY ++ [Move], MovesX, [], Move, 10000) + calculate(generate_point(vertical, Move), MovesY ++ [Move], MovesX, [], Move, 10000) + calculate(generate_point(fdiagonal, Move), MovesY ++ [Move], MovesX, [], Move, 10000) + calculate(generate_point(sdiagonal, Move), MovesY ++ [Move], MovesX, [], Move, 10000), PGravity = PGravityY + Aggress * PGravityX, [{PGravity, Move}] ++ calculate_point_gravity(MovesX, MovesY, Rest, Aggress). loop(_,_,_,0, Counter) -> Counter; loop([],_,_,_, Counter) -> Counter; loop(_,_,_,_, opponent_point_find) -> 0; loop([FC | RC], MovesX, MovesY, Num, Counter) -> Res = case exist_in_list(MovesX, FC) of true -> Counter + 1; %   false -> %    case exist_in_list(MovesY, FC) of true -> opponent_point_find; %     false -> Counter % ,  end end, loop(RC ,MovesX, MovesY, Num - 1, Res). calculate(CList, MovesX, MovesY, Current, BreakElement, W) when Current == BreakElement -> 0; calculate(CList, MovesX, MovesY, Current, BreakElement, W) -> Res = loop(CList, MovesX, MovesY, 5, 0) NewRes = case Res of opponent_point_find -> 0; 0 -> 0; 1 -> 0; % 1   5 -> W; %    5, _ -> math:pow(3, Res) %      end, [Head | Rest] = CList, NewRes + calculate(Rest, MovesX, MovesY, Head, BreakElement, W). 

I want to note that in the functions calculate and calculate_point_gravity, tail recursion is not used, I do not think that this will somehow affect performance or memory consumption, due to the fact that the number of iterations is negligible.



When we calculated the coefficient of effectiveness for each cell, we choose the highest one:

 lists:max(calculate_point_gravity(PlayerMovesX , PlayerMovesY, AllVariants, Agress)). 

You can still add chance, but I found it redundant.

Check

Any game loses its meaning, without determining two sides: the winner and the loser, but sometimes also the variant with a draw.



Now let's take a quick look at the win check algorithm, the check is initialized after each subsequent player move, and checks 3 outcomes in turn: player win, bot win, draw, the check function takes 2 arguments at the input, 1 - all the steps made by the player, 2 - the last player move.







The picture shows the basic algorithm (there are 8 rays in all directions, due to compression it is not visible) - viewing all cells with the current symbol and increasing the counter value, but with a small nuance, each of the 4 directions is divided into two parts: the upper and the lower, after checking both parts, perform the summation and add one, if the sum is equal to 5, the winning sequence is found.

Rest

And of course, the demo:



http://88.198.65.2:8000/



The complexity of the game is dynamic, you can change it until the next turn, by default - 0.8, the greater the difficulty coefficient - the bot goes into a defensive strategy, the less - the attack strategy, I advise you to experiment with complexity, I think the bot plays quite well within [0.5 , one].



I apologize in advance to people who are behind a proxy, or those who have port 8000 closed, I now have no opportunity to transfer the game to port 80.



Sources are available on github'e - github.com/Tremax/eTicTacToe



I do not consider the client part, due to the fact that everything is trivial there.

Links

algolist.manual.ru/games/fiveinarow.php



I will be glad to hear your feedback.