Implementing the k-means algorithm on c # (with a generalized metric)
Hello. Continuing the topic that Andrew Ng did not have time to tell in the course on machine learning , I will give an example of my own implementation of the k-means algorithm. My task was to implement the clustering algorithm, but I needed to take into account the degree of correlation between the quantities. I decided to use the Mahalanobis distance as a metric, I note that the size of the data for clustering is not so large, and there was no need to do caching of clusters to disk. For implementation, please under the cat.
To begin, consider the problem, why not just replace the Euclidean distance with any other metric. The k-means algorithm uses two parameters for input: the data for clustering and the number of clusters into which the data should be split. The algorithm consists of the following steps.
')
For understanding mathematics, which is behind this simple algorithm, I advise you to read articles on Bayesian clustering and the expectation-maximization algorithm .
The problem of replacing the Euclidean distance by another metric is in the M-step. For example, if we have textual data and use Levenshtein distance as a metric, then finding the average value is not an entirely trivial task. For me, even finding the Mahalanobis average was not a quickly solvable problem, but I was lucky and I came across an article that described a very simple way to select the “centroid”, and I did not have to puzzle over the Mahalanobis average value. In quotation marks, because the exact value of the centroid is not searched for, but its approximate value is chosen, which in that article is called clusteroid (or, by analogy with k-medoids, it can be called a medoid). Thus, the maximization step is replaced by the following algorithm.
By the way, for me the question of convergence is still open, but the good, there are many ways to stop the algorithm at some suboptimal solution. In this implementation, we will stop the algorithm if the cost function begins to grow.
The cost function for the current partition will use the following formula: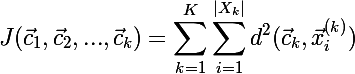
where K is the number of clusters, 
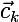- the current center of the cluster, 
- the set of elements assigned to cluster k, and 
- i-th element of the cluster k.
Regarding the search for the average distance, it is worth noting that if the metric function is continuous and differentiable, then to search for the clusteroid you can use the gradient descent algorithm , which minimizes the following cost function: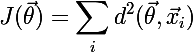
, where X's are elements related to the current cluster. I plan to consider this option in the next article, but for now in the implementation we will take into account that some method will soon add its own way to search for a centroid / clusteroid.
First, let's create a general metric representation and then implement the common logic and concrete implementation of several metrics.
Thus, the metric is abstracted from the data type and we will be able to implement it both the Euclidean distance between the numerical vectors and the Levenshtein distance between the lines and sentences.
Now we will create a base class for metrics in which we implement the function of searching for the clusteroid using a simple method described above.
In the GetCentroid method, we are looking for an element for which the sum of squares of distances to the remaining data elements is minimal. First we create a symmetric matrix, in which the elements contain the distances between the corresponding data elements. Using the properties of metrics: d (x, x) = 0 and d (x, y) = d (y, x), we can safely fill the diagonal with zeros and reflect the matrix along the main diagonal. Then we sum up in the lines and we look for the minimum value.
For example, let's create an implementation of the distances of Mahalanobis and Euclid.
As you can see from the code, the GetCentroid method is not redefined, although in the next article I will try to override this method with a gradient descent algorithm.
In the implementation of the Euclidean distance, the GetCentroid method is redefined, and searches for the exact centroid value: the average values of each of the coordinates are calculated.
Let's proceed to the implementation of the clustering algorithm. Again, first create an interface for clustering algorithms.
Where the result of clustering is as follows:
And the item class:
We are interested only in the Input property, since it is learning without a teacher.
Let us turn to the implementation of the k-means algorithm using the above interfaces.
The following data is fed into the clustering algorithm (I have reduced my code a little so as not to bother with the initialization methods of the initial centroids, we will use random initialization of points, we can afford it here, because we cluster the
Problem
To begin, consider the problem, why not just replace the Euclidean distance with any other metric. The k-means algorithm uses two parameters for input: the data for clustering and the number of clusters into which the data should be split. The algorithm consists of the following steps.
- Initial initialization of cluster centroids in some way (for example, you can set initial values by randomly selected points from the space in which data is defined; random points can be selected from the input data array, etc.).
- E-step ( expectation ): an association occurs between data elements and clusters, which are represented as their centers (centroids).
- M-step ( maximization ): centers of clusters are recalculated as average values of data that were included with the corresponding cluster (or, in other words, the model parameters are modified in such a way as to maximize the probability that the element will fall into the selected cluster). If the cluster after step 2 was empty, then it is reinitialized in some other way.
- Steps 2-3 are repeated until convergence, or until another criterion for stopping the algorithm is reached (for example, if a certain number of iterations is exceeded).
')
For understanding mathematics, which is behind this simple algorithm, I advise you to read articles on Bayesian clustering and the expectation-maximization algorithm .
The problem of replacing the Euclidean distance by another metric is in the M-step. For example, if we have textual data and use Levenshtein distance as a metric, then finding the average value is not an entirely trivial task. For me, even finding the Mahalanobis average was not a quickly solvable problem, but I was lucky and I came across an article that described a very simple way to select the “centroid”, and I did not have to puzzle over the Mahalanobis average value. In quotation marks, because the exact value of the centroid is not searched for, but its approximate value is chosen, which in that article is called clusteroid (or, by analogy with k-medoids, it can be called a medoid). Thus, the maximization step is replaced by the following algorithm.
- M-step: among all data elements that were assigned to the centroid, the element is selected for which the sum of the distances to all other cluster elements is minimal; this element becomes the new cluster center.
By the way, for me the question of convergence is still open, but the good, there are many ways to stop the algorithm at some suboptimal solution. In this implementation, we will stop the algorithm if the cost function begins to grow.
The cost function for the current partition will use the following formula:
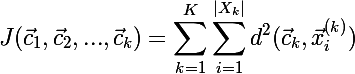where K is the number of clusters, 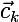- the current center of the cluster, - the set of elements assigned to cluster k, and - i-th element of the cluster k.Regarding the search for the average distance, it is worth noting that if the metric function is continuous and differentiable, then to search for the clusteroid you can use the gradient descent algorithm , which minimizes the following cost function:
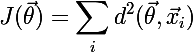, where X's are elements related to the current cluster. I plan to consider this option in the next article, but for now in the implementation we will take into account that some method will soon add its own way to search for a centroid / clusteroid.Metrics
First, let's create a general metric representation and then implement the common logic and concrete implementation of several metrics.
public interface IMetrics<T> { double Calculate(T[] v1, T[] v2); T[] GetCentroid(IList<T[]> data); } Thus, the metric is abstracted from the data type and we will be able to implement it both the Euclidean distance between the numerical vectors and the Levenshtein distance between the lines and sentences.
Now we will create a base class for metrics in which we implement the function of searching for the clusteroid using a simple method described above.
public abstract class MetricsBase<T> : IMetrics<T> { public abstract double Calculate(T[] v1, T[] v2); public virtual T[] GetCentroid(IList<T[]> data) { if (data == null) { throw new ArgumentException("Data is null"); } if (data.Count == 0) { throw new ArgumentException("Data is empty"); } double[][] dist = new double[data.Count][]; for (int i = 0; i < data.Count - 1; i++) { dist[i] = new double[data.Count]; for (int j = i; j < data.Count; j++) { if (i == j) { dist[i][j] = 0; } else { dist[i][j] = Math.Pow(Calculate(data[i], data[j]), 2); if (dist[j] == null) { dist[j] = new double[data.Count]; } dist[j][i] = dist[i][j]; } } } double minSum = Double.PositiveInfinity; int bestIdx = -1; for (int i = 0; i < data.Count; i++) { double dSum = 0; for (int j = 0; j < data.Count; j++) { dSum += dist[i][j]; } if (dSum < minSum) { minSum = dSum; bestIdx = i; } } return data[bestIdx]; } } In the GetCentroid method, we are looking for an element for which the sum of squares of distances to the remaining data elements is minimal. First we create a symmetric matrix, in which the elements contain the distances between the corresponding data elements. Using the properties of metrics: d (x, x) = 0 and d (x, y) = d (y, x), we can safely fill the diagonal with zeros and reflect the matrix along the main diagonal. Then we sum up in the lines and we look for the minimum value.
For example, let's create an implementation of the distances of Mahalanobis and Euclid.
internal class MahalanobisDistanse : MetricsBase<double> { private double[][] _covMatrixInv = null; internal MahalanobisDistanse(double[][] covMatrix, bool isInversed) { if (!isInversed) { _covMatrixInv = LinearAlgebra.InverseMatrixGJ(covMatrix); } else { _covMatrixInv = covMatrix; } } public override double Calculate(double[] v1, double[] v2) { if (v1.Length != v2.Length) { throw new ArgumentException("Vectors dimensions are not same"); } if (v1.Length == 0 || v2.Length == 0) { throw new ArgumentException("Vector dimension can't be 0"); } if (v1.Length != _covMatrixInv.Length) { throw new ArgumentException("CovMatrix and vectors have different size"); } double[] delta = new double[v1.Length]; for (int i = 0; i < v1.Length; i++) { delta[i] = v1[i] - v2[i]; } double[] deltaS = new double[v1.Length]; for (int i = 0; i < deltaS.Length; i++) { deltaS[i] = 0; for (int j = 0; j < v1.Length; j++) { deltaS[i] += delta[j]*_covMatrixInv[j][i]; } } double d = 0; for (int i = 0; i < v1.Length; i++) { d += deltaS[i]*delta[i]; } d = Math.Sqrt(d); return d; } } As you can see from the code, the GetCentroid method is not redefined, although in the next article I will try to override this method with a gradient descent algorithm.
internal class EuclideanDistance : MetricsBase<double> { internal EuclideanDistance() { } #region IMetrics Members public override double Calculate(double[] v1, double[] v2) { if (v1.Length != v2.Length) { throw new ArgumentException("Vectors dimensions are not same"); } if (v1.Length == 0 || v2.Length == 0) { throw new ArgumentException("Vector dimension can't be 0"); } double d = 0; for (int i = 0; i < v1.Length; i++) { d += (v1[i] - v2[i]) * (v1[i] - v2[i]); } return Math.Sqrt(d); } public override double[] GetCentroid(IList<double[]> data) { if (data.Count == 0) { throw new ArgumentException("Data is empty"); } double[] mean = new double[data.First().Length]; for (int i = 0; i < mean.Length; i++) { mean[i] = 0; } foreach (double[] item in data) { for (int i = 0; i < item.Length; i++) { mean[i] += item[i]; } } for (int i = 0; i < mean.Length; i++) { mean[i] = mean[i]/data.Count; } return mean; } #endregion } In the implementation of the Euclidean distance, the GetCentroid method is redefined, and searches for the exact centroid value: the average values of each of the coordinates are calculated.
Clustering
Let's proceed to the implementation of the clustering algorithm. Again, first create an interface for clustering algorithms.
public interface IClusterization<T> { ClusterizationResult<T> MakeClusterization(IList<DataItem<T>> data); } Where the result of clustering is as follows:
public class ClusterizationResult<T> { public IList<T[]> Centroids { get; set; } public IDictionary<T[], IList<DataItem<T>>> Clusterization { get; set; } public double Cost { get; set; } } And the item class:
public class DataItem<T> { private T[] _input = null; private T[] _output = null; public DataItem(T[] input, T[] output) { _input = input; _output = output; } public T[] Input { get { return _input; } } public T[] Output { get { return _output; } set { _output = value; } } } We are interested only in the Input property, since it is learning without a teacher.
Let us turn to the implementation of the k-means algorithm using the above interfaces.
internal class KMeans : IClusterization<double> The following data is fed into the clustering algorithm (I have reduced my code a little so as not to bother with the initialization methods of the initial centroids, we will use random initialization of points, we can afford it here, because we cluster the
IClusterization):
clusterCount - IMetrics metrics -
IClusterization):
clusterCount - IMetrics metrics -
IClusterization):
clusterCount - IMetrics metrics -
IClusterization):-
clusterCountIMetrics metrics -IClusterization):-
clusterCountIMetrics metrics -
Source: https://habr.com/ru/post/146556/
All Articles