A simple example of encoding a text string according to Huffman
You've probably heard about David Huffman and his popular compression algorithm. If not, then I suggest you search on the Internet yourself - in this article I will not pester you with the lessons of history or mathematics. I will try to show you in practice how to apply this algorithm to a text string. Our application will simply generate the code values for the characters from the entered string and set it - it will recreate the original string from the presented code.
The idea of Huffman coding is based on the frequency of use of characters in a string. The most common character needs to give the shortest possible code value, and the least frequently found one as long as possible. Due to the fact that during archiving, the most frequently encountered characters should occupy less space than before, and the least frequently encountered can occupy more space - if there are few of them, this will not greatly affect the result.
For our example, I decided to make the symbol 8-bit, i.e. type char. With the same success it was possible to choose the length and sixteen, ten or twenty bits. The length of the symbol should be chosen depending on the expected input data. For example, for encoding video files, I would select a character the same size as the pixel. Keep in mind that increasing or decreasing the length of a character affects the length of the code for each of the characters - the longer the length, the more characters of this length can exist: the ways to write ones and zeros in eight bits are much less than sixteen. Therefore, the length of the character must be adjusted depending on the task.
The Huffman algorithm actively uses binary trees and priority queues , so if you are not familiar with them, you will have to fill in the knowledge gaps first.
')
Suppose we have the string “beep boop beer!”, Which takes 15 * 8 = 120 bits in memory. After Huffman coding, this size can be reduced to 40 bits. If you find fault with the details, we will display a string consisting of 40 char elements (zeros and ones), and in order for it to occupy exactly 40 bits in memory, this string needs to be converted into bits using binary arithmetic operations, which we will not here consider in detail.
So, consider the string "beep boop beer!". To construct code values for all elements depending on their frequency, you need to build such a binary tree, in which each sheet contains a symbol from a given string. We will build a tree from leaves to the root, so that the elements with a smaller frequency are farther from the root, and the more frequent ones are closer to it. Find out soon why.
For the construction of such a tree, we will use the priority queue, but with a slightly modified queue - we invert priorities so that the element with the lowest priority is the most important. It turns out that the queue will first return the elements with the least frequency. This modification will help us build a tree starting from the leaves.
First, let's calculate the frequency of each symbol:
After that, we will create elements of the binary tree for each symbol and represent them as a queue with priority, for which we will use the frequency.

Now take the first two items from the queue and create the third one, which will be their parent. We will place this new item in a queue with a priority equal to the sum of the priorities of its two descendants. In other words, equal to the sum of their frequencies.

Further we will repeat the steps similar to the previous one:

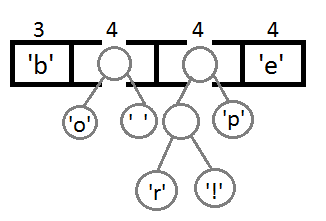
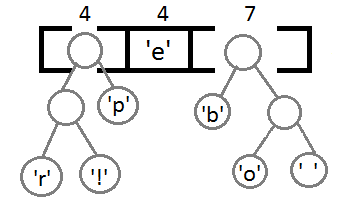

Now, after combining the last two elements with the help of their new parent, we get the final binary tree:

It remains to assign each character its code. To do this, we will launch a detour into the depth and each time, considering the right subtree, we will write to code 1, and considering the left subtree - 0.
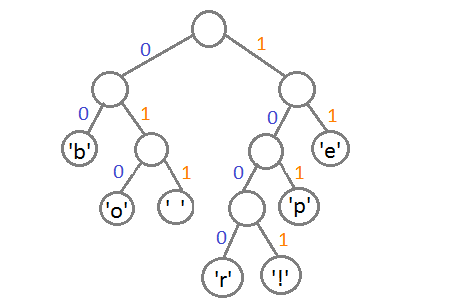
As a result, the correspondence between symbols and code values is obtained as follows:
Decoding a sequence of bits is very simple: you need to bypass the tree, discarding the left subtree, if one is encountered and right, if it is 0. You need to continue traversing until you meet the sheet, i.e. The value of the encoded character. For example, the encoded string “101 11 101 11” and our decoding tree correspond to the string “pepe”.
It is important to note here that no code value is a prefix of any other. In our example, 00 is the character code “b”. This means that 000 can no longer be a code for any other character, since otherwise, it would lead to conflict when decoding. After all, if, after passing through 00, we came to the “b” sheet, then by the code value 000, we will not find any other symbol.
In practice, after generating the Huffman tree, you also need to construct a Huffman table. A table (in the form of a coherent list or array) will make the coding procedure more efficient, because finding a symbol in the tree and simultaneously recording its code is unnecessarily time consuming. Since we do not know for sure where this symbol is located, at worst we will have to search through the whole tree in its search. As a rule, the Huffman table is used for encoding, and the Huffman tree is used for decoding.
Input string: beep boop beer!
Input string in binary form: 0110 0010 0110 0101 0110 0101 0111 0000 0010 0000 0110 0010 0110 1111 0110 1111 0111 0000 0010 0000 0110 0010 0110 0101 0110 0101 0111 0010 0010 0001
Encoded line: 0011 1110 1011 0001 0010 1010 1100 1111 1000 1001
It is easy to notice the significant difference between the ASCII-coding of the string and its appearance in the Huffman code.
It should be noted that the article only explains the principle of the algorithm. For practical use, you will have to add a Huffman tree to the beginning or end of the encoded sequence. The recipient of the message must know how to separate the tree from the content and how to restore it from the textual representation. A good way to do this is to bypass the tree in any pre-selected order, writing 0 for each non-leaf item encountered, and 1 for each leaf. Following the unit, you can write the source symbol (in our case, the char type, 8 bits in ASCII). A tree recorded in this form can be placed at the beginning of the coded sequence — then the recipient, having built the tree at the very beginning of the analysis, will already know how to decode the message written further and get the original from it.
Read about a more advanced version of the algorithm, you can in the article " Adaptive Huffman coding ."
PS (from translator)
Thank you bobuk for giving the link to the original article in your linkblog .
The idea of Huffman coding is based on the frequency of use of characters in a string. The most common character needs to give the shortest possible code value, and the least frequently found one as long as possible. Due to the fact that during archiving, the most frequently encountered characters should occupy less space than before, and the least frequently encountered can occupy more space - if there are few of them, this will not greatly affect the result.
For our example, I decided to make the symbol 8-bit, i.e. type char. With the same success it was possible to choose the length and sixteen, ten or twenty bits. The length of the symbol should be chosen depending on the expected input data. For example, for encoding video files, I would select a character the same size as the pixel. Keep in mind that increasing or decreasing the length of a character affects the length of the code for each of the characters - the longer the length, the more characters of this length can exist: the ways to write ones and zeros in eight bits are much less than sixteen. Therefore, the length of the character must be adjusted depending on the task.
The Huffman algorithm actively uses binary trees and priority queues , so if you are not familiar with them, you will have to fill in the knowledge gaps first.
')
Suppose we have the string “beep boop beer!”, Which takes 15 * 8 = 120 bits in memory. After Huffman coding, this size can be reduced to 40 bits. If you find fault with the details, we will display a string consisting of 40 char elements (zeros and ones), and in order for it to occupy exactly 40 bits in memory, this string needs to be converted into bits using binary arithmetic operations, which we will not here consider in detail.
So, consider the string "beep boop beer!". To construct code values for all elements depending on their frequency, you need to build such a binary tree, in which each sheet contains a symbol from a given string. We will build a tree from leaves to the root, so that the elements with a smaller frequency are farther from the root, and the more frequent ones are closer to it. Find out soon why.
For the construction of such a tree, we will use the priority queue, but with a slightly modified queue - we invert priorities so that the element with the lowest priority is the most important. It turns out that the queue will first return the elements with the least frequency. This modification will help us build a tree starting from the leaves.
First, let's calculate the frequency of each symbol:
| Symbol | Frequency |
|---|---|
| 'b' | 3 |
| 'e' | four |
| 'p' | 2 |
| '' | 2 |
| 'o' | 2 |
| 'r' | one |
| '!' | one |
After that, we will create elements of the binary tree for each symbol and represent them as a queue with priority, for which we will use the frequency.

Now take the first two items from the queue and create the third one, which will be their parent. We will place this new item in a queue with a priority equal to the sum of the priorities of its two descendants. In other words, equal to the sum of their frequencies.

Further we will repeat the steps similar to the previous one:




Now, after combining the last two elements with the help of their new parent, we get the final binary tree:

It remains to assign each character its code. To do this, we will launch a detour into the depth and each time, considering the right subtree, we will write to code 1, and considering the left subtree - 0.

As a result, the correspondence between symbols and code values is obtained as follows:
| Sivol | Code value |
|---|---|
| 'b' | 00 |
| 'e' | eleven |
| 'p' | 101 |
| '' | 011 |
| 'o' | 010 |
| 'r' | 1000 |
| '!' | 1001 |
Decoding a sequence of bits is very simple: you need to bypass the tree, discarding the left subtree, if one is encountered and right, if it is 0. You need to continue traversing until you meet the sheet, i.e. The value of the encoded character. For example, the encoded string “101 11 101 11” and our decoding tree correspond to the string “pepe”.
It is important to note here that no code value is a prefix of any other. In our example, 00 is the character code “b”. This means that 000 can no longer be a code for any other character, since otherwise, it would lead to conflict when decoding. After all, if, after passing through 00, we came to the “b” sheet, then by the code value 000, we will not find any other symbol.
In practice, after generating the Huffman tree, you also need to construct a Huffman table. A table (in the form of a coherent list or array) will make the coding procedure more efficient, because finding a symbol in the tree and simultaneously recording its code is unnecessarily time consuming. Since we do not know for sure where this symbol is located, at worst we will have to search through the whole tree in its search. As a rule, the Huffman table is used for encoding, and the Huffman tree is used for decoding.
Input string: beep boop beer!
Input string in binary form: 0110 0010 0110 0101 0110 0101 0111 0000 0010 0000 0110 0010 0110 1111 0110 1111 0111 0000 0010 0000 0110 0010 0110 0101 0110 0101 0111 0010 0010 0001
Encoded line: 0011 1110 1011 0001 0010 1010 1100 1111 1000 1001
It is easy to notice the significant difference between the ASCII-coding of the string and its appearance in the Huffman code.
It should be noted that the article only explains the principle of the algorithm. For practical use, you will have to add a Huffman tree to the beginning or end of the encoded sequence. The recipient of the message must know how to separate the tree from the content and how to restore it from the textual representation. A good way to do this is to bypass the tree in any pre-selected order, writing 0 for each non-leaf item encountered, and 1 for each leaf. Following the unit, you can write the source symbol (in our case, the char type, 8 bits in ASCII). A tree recorded in this form can be placed at the beginning of the coded sequence — then the recipient, having built the tree at the very beginning of the analysis, will already know how to decode the message written further and get the original from it.
Read about a more advanced version of the algorithm, you can in the article " Adaptive Huffman coding ."
PS (from translator)
Thank you bobuk for giving the link to the original article in your linkblog .
Source: https://habr.com/ru/post/146346/
All Articles