I can not write a binary search
Recently (literally two years ago) an article ran through here. Only 10% of programmers are able to write a binary search . Binary search is a classic search algorithm. Moreover, it is still an extremely simple algorithm that can be very easily described: take a sorted array, look in the middle, if you do not find a number there, depending on what is in the middle - we are looking for this number using the same method either on the left side or on the right, tilting the middle element. For functions also, we simply take not an array, but a function. Everything is very, very simple, the algorithm is described almost everywhere, all the bugs are recorded and described.
So, I can not implement a binary search. For me, he is not a bit trivial. I guess I'm not a real programmer. But it is, I am only a student, but this is no excuse? More specifically, I cannot implement a good, correct, beautiful binary search. All the time, the problem comes to me either with correctness, or with prettiness, or with both. So, yes, the title is a little yellowish.
Before reading this topic, write your version of the binary search - for a sorted array. Moreover, depending on the parameter, the search should produce either the first element or any of the duplicates. For comparison, write a binary search for functions
For starters, I will write C # code. I hope fans of other languages will easily understand my code. I will represent the boundaries of the search in the form of a half-interval [left; right) i.e. the left point is turned on, and the right point is turned off. For me, the intervals are more convenient, I’m already used to their behavior, and besides, the use of half-intervals has some advantages when programming various algorithms (which we will talk about later). In general, it is more correct to use half-intervals in terms of supporting the “common programming style”, as I write loops like this:
, , . :
, . , . , ,
, . off-by-one. , :
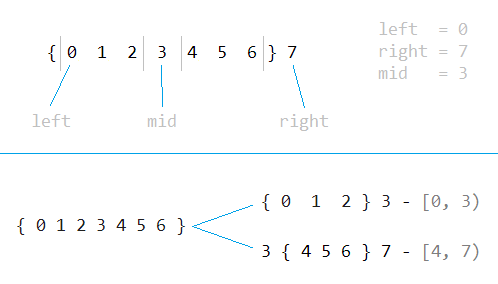
, [0, 3) [4, 7), .. [left, mid) [mid + 1, right). , «» ( ), , , , . , , , , .
, : [left, right], [left, mid — 1] [mid + 1; right] ( , , ).
1 ( , ), — 2 — , .
, ( [left, mid) [mid, right)), 1 ( [left, mid] [mid + 1, right], [left, mid — 1] [mid, right]).
, , , , (array[mid]), (key). — , , , , :-). - . , , «».
, , . - , ? - . ? ( , -1)? int int? null? (int? c# — , null). , - , ? - ? … , « ?». , , : , . , , , null, null.
-(1 + left), , , , . , — , . DRY, - , . , .
, left == right, .., — [left, right). , right — left < 1 right — left <= 0. , , , - ( , ).
, . ||, &&, , XOR':
.. descendingOrder , , , . «», , - . , .
, . «» — , . , , … .
, , :
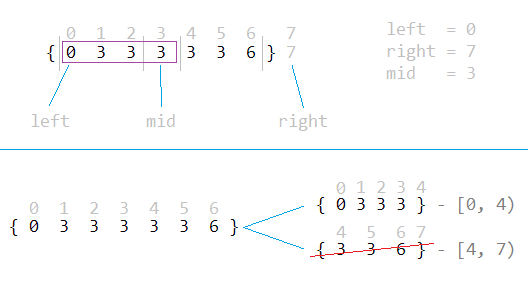
, , , . , , . , , . (. )
, , , , . , , :
, ? , 3 , ? , , , ( ).
, , / getFirstHalf, getSecondHalf ( ), getStartPoint/getLastPoint ( / ), increaseLength/decreaseLength ( ), moveStartPoint. - . , .
, , . … , « », . :
. ? ? float'? ( , ?, , - ).
? left; right? [left, right], [left, right), (left, right], (left, right)? . :
, left . right (). .. a b, a, b, - . .
, , , mid /. .
- , func(left) == key func(right) == key, .
, : , .
, , - . , - .
, - , : , — , a/b. : a b . -: O(lgn).
, : - — , // , , ?
P.S: , . ,
P.P.S: ?
UPD1: fox_anthony -(1 + left) ~left. : ~, msdn, c#
So, I can not implement a binary search. For me, he is not a bit trivial. I guess I'm not a real programmer. But it is, I am only a student, but this is no excuse? More specifically, I cannot implement a good, correct, beautiful binary search. All the time, the problem comes to me either with correctness, or with prettiness, or with both. So, yes, the title is a little yellowish.
Before reading this topic, write your version of the binary search - for a sorted array. Moreover, depending on the parameter, the search should produce either the first element or any of the duplicates. For comparison, write a binary search for functions
For starters, I will write C # code. I hope fans of other languages will easily understand my code. I will represent the boundaries of the search in the form of a half-interval [left; right) i.e. the left point is turned on, and the right point is turned off. For me, the intervals are more convenient, I’m already used to their behavior, and besides, the use of half-intervals has some advantages when programming various algorithms (which we will talk about later). In general, it is more correct to use half-intervals in terms of supporting the “common programming style”, as I write loops like this:
for (int i = 0; i < array.Length; i++)for (int i = 0; i <= array.Length - 1; i++), , . :
static int BinarySearch_Rec_Wrapper(int[] array, int element)
{
BinarySearch_Rec(array, element, 0, array.Length);
}, . , . , ,
int mid = (left + right) / 2 int mid = left + (right - left) / 2, . off-by-one. , :

, [0, 3) [4, 7), .. [left, mid) [mid + 1, right). , «» ( ), , , , . , , , , .
, : [left, right], [left, mid — 1] [mid + 1; right] ( , , ).
1 ( , ), — 2 — , .
, ( [left, mid) [mid, right)), 1 ( [left, mid] [mid + 1, right], [left, mid — 1] [mid, right]).
, , , , (array[mid]), (key). — , , , , :-). - . , , «».
:
static int BinarySearch_Rec(int[] array, int key, int left, int right)
{
int mid = left + (right - left) / 2;
if (array[mid] == key)
return mid;
else if (array[mid] > key)
return BinarySearch_Rec(array, key, left, mid);
else
return BinarySearch_Rec(array, key, mid + 1, right);
}
:
static int BinarySearch_Iter(int[] array, int key)
{
int left = 0;
int right = array.Length;
while (true)
{
int mid = left + (right - left) / 2;
if (array[mid] == key)
return mid;
if (array[mid] > key)
right = mid;
else
left = mid + 1;
}
}
:
, , , . while(true), , . , , . , ., , . - , ? - . ? ( , -1)? int int? null? (int? c# — , null). , - , ? - ? … , « ?». , , : , . , , , null, null.
-(1 + left), , , , . , — , . DRY, - , . , .
, left == right, .., — [left, right). , right — left < 1 right — left <= 0. , , , - ( , ).
:
static int BinarySearch_Rec(int[] array, int key, int left, int right)
{
int mid = left + (right - left) / 2;
if (left >= right)
return -(1 + left);
if (array[mid] == key)
return mid;
else if (array[mid] > key)
return BinarySearch_Rec(array, key, left, mid);
else
return BinarySearch_Rec(array, key, mid + 1, right);
}
:
static int BinarySearch_Iter(int[] array, int key)
{
int left = 0;
int right = array.Length;
int mid = 0;
while (!(left >= right))
{
mid = left + (right - left) / 2;
if (array[mid] == key)
return mid;
if (array[mid] > key)
right = mid;
else
left = mid + 1;
}
return -(1 + left);
}
:
, . , , . , - , .№3
, . ||, &&, , XOR':
| descendingOrder | array[mid] > key | XOR |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
.. descendingOrder , , , . «», , - . , .
:
static int BinarySearch_Rec(int[] array, bool descendingOrder, int key, int left, int right)
{
int mid = left + (right - left) / 2;
if (left >= right)
return -(1 + left);
if (array[mid] == key)
return mid;
else if ((array[mid] > key) ^ descendingOrder)
return BinarySearch_Rec(array, descendingOrder, key, left, mid);
else
return BinarySearch_Rec(array, descendingOrder, key, mid + 1, right);
}
static int BinarySearch_Rec_Wrapper(int[] array, int key)
{
if (array.Length == 0)
return -1;
bool descendingOrder = array[0] > array[array.Length - 1];
return BinarySearch_Rec(array, descendingOrder, key, 0, array.Length);
}
:
static int BinarySearch_Iter(int[] array, bool descendingOrder, int key)
{
int left = 0;
int right = array.Length;
int mid = 0;
while (!(left >= right))
{
mid = left + (right - left) / 2;
if (array[mid] == key)
return mid;
if ((array[mid] > key) ^ descendingOrder)
right = mid;
else
left = mid + 1;
}
return -(1 + left);
}
static int BinarySearch_Iter_Wrapper(int[] array, int key)
{
if (array.Length == 0)
return -1;
bool descendingOrder = array[0] > array[array.Length - 1];
return BinarySearch_Iter(array, descendingOrder, key);
}
:
: , . .№4
, . «» — , . , , … .
, , :

, , , . , , . , , . (. )
:
static int BinarySearch_Rec(int[] array, bool descendingOrder, int key, int left, int right)
{
int mid = left + (right - left) / 2;
if (left >= right)
return -(1 + left);
if (array[left] == key)
return left;
if (array[mid] == key)
{
if (mid == left + 1)
return mid;
else
return BinarySearch_Rec(array, descendingOrder, key, left, mid + 1);
}
else if ((array[mid] > key) ^ descendingOrder)
return BinarySearch_Rec(array, descendingOrder, key, left, mid);
else
return BinarySearch_Rec(array, descendingOrder, key, mid + 1, right);
}
static int BinarySearch_Rec_Wrapper(int[] array, int key)
{
if (array.Length == 0)
return -1;
bool descendingOrder = array[0] > array[array.Length - 1];
return BinarySearch_Rec(array, descendingOrder, key, 0, array.Length);
}
:
static int BinarySearch_Iter(int[] array, bool descendingOrder, int key)
{
int left = 0;
int right = array.Length;
int mid = 0;
while (!(left >= right))
{
mid = left + (right - left) / 2;
if (array[left] == key)
return left;
if (array[mid] == key)
{
if (mid == left + 1)
return mid;
else
right = mid + 1;
}
else if ((array[mid] > key) ^ descendingOrder)
right = mid;
else
left = mid + 1;
}
return -(1 + left);
}
static int BinarySearch_Iter_Wrapper(int[] array, int key)
{
if (array.Length == 0)
return -1;
bool descendingOrder = array[0] > array[array.Length - 1];
return BinarySearch_Iter(array, descendingOrder, key);
}
№5
, , , , . , , :
?
?
enum ElementToChoose
{
First,
Last,
NoCare
}
/// <summary>
/// Finds element equal to value in sorted array in range [low, high)
/// </summary>
static int binarySearch(int value, int[] array, bool ascendingOrder, ElementToChoose elementToChoose, int low, int high) {
// return valid invalid position
if (low >= high)
return -(low + 1);
// return first or last found element
if (elementToChoose == ElementToChoose.First)
if (value == array[low])
return low;
int last = high - 1;
if (elementToChoose == ElementToChoose.Last)
if (value == array[last])
return last;
int mid = low + (high - low) / 2;
// we have found some element
if (value == array[mid]) {
switch (elementToChoose) {
case ElementToChoose.NoCare:
return mid;
case ElementToChoose.First:
if (mid - low <= 1)
// array[mid] is the earliest element in array, return it
// because array[low] != value && array[low+1] == value, where mid == low + 1
return mid;
else
// try to find first element
// don't forget to capture current element {|0, 0|, 1} -> {0, 0}
return binarySearch(value, array, ascendingOrder, elementToChoose, low, mid + 1);
case ElementToChoose.Last:
if (last - mid <= 1)
// array[mid] is the last element in array, return it
// because array[last] != value && array[last - 1] == value, where mid == last - 1
return mid;
else
// try to find last element
// don't forget to capture current element {0, |0, 1|} -> {0, 1}
return binarySearch(value, array, ascendingOrder, elementToChoose, mid, high);
}
}
// choose left or right half, depending on sorting order & comparing value and mid
if ((value < array[mid]) ^ !ascendingOrder)
return binarySearch(value, array, ascendingOrder, elementToChoose, low, mid);
else
return binarySearch(value, array, ascendingOrder, elementToChoose, mid + 1, high);
}
, ? , 3 , ? , , , ( ).
, , / getFirstHalf, getSecondHalf ( ), getStartPoint/getLastPoint ( / ), increaseLength/decreaseLength ( ), moveStartPoint. - . , .
, , . … , « », . :
// - Func<float, float> , float float
static float BinarySearch_Func(Func<float, float> func, bool descendingOrder, float key, float left, float right)
{
float mid = (left + right) / 2;
if (left == mid || mid == right)
return mid;
if ((func(mid) > key) ^ descendingOrder)
return BinarySearch_Func(func, descendingOrder, key, left, mid);
else
return BinarySearch_Func(func, descendingOrder, key, mid, right);
}
static float BinarySearch_Func_Wrapper(Func<float, float> func, float key, float left, float right)
{
if (left > right)
return float.NaN;
bool descendingOrder = func(left) > func(right);
bool isOk = true;
if (!descendingOrder)
isOk = func(left) <= key && key <= func(right);
else
isOk = func(right) <= key && key <= func(left);
if (isOk)
return BinarySearch_Func(func, descendingOrder, key, left, right);
else
return float.NaN;
}
. ? ? float'? ( , ?, , - ).
? left; right? [left, right], [left, right), (left, right], (left, right)? . :
// x => x - - f(x) = x
Console.WriteLine(BinarySearch_Func_Wrapper(x => x, 0.7f, 0.7f, 100.0f)); // : 0.7
Console.WriteLine(BinarySearch_Func_Wrapper(x => x, 0.8f, 0.8f, 100.0f)); // : 0,8000001
Console.WriteLine(BinarySearch_Func_Wrapper(x => x, 0.9f, 0.9f, 100.0f)); // : 0,9
Console.WriteLine("{0:0.00000000}",0.8f); // : 0,80000000
, left . right (). .. a b, a, b, - . .
, , , mid /. .
- , func(left) == key func(right) == key, .
, : , .
, , - . , - .
, - , : , — , a/b. : a b . -: O(lgn).
, : - — , // , , ?
P.S: , . ,
P.P.S: ?
UPD1: fox_anthony -(1 + left) ~left. : ~, msdn, c#
')
Source: https://habr.com/ru/post/146228/
All Articles