Soft integrals
Some of you have probably seen this problem in the open spaces of the network: what number is the next row going on?
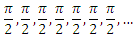
This obvious correct answer was suggested:
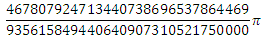
For those to whom it is not obvious how it was received, an explanation was offered. Let be
(well, 1 for x = 0, although it does not matter). Then each member of the series is the value of the following integral in the chain:
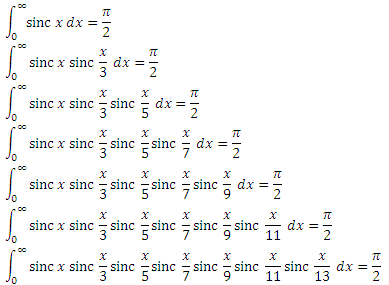
So far everything is going well, but then suddenly:
In principle, this is enough to amuse fellow mathematicians, but I wanted to know how such integrals are generally considered and why such a ridiculous result is obtained. If someone else wants to shake the old days and remember the matan with the function, please read on.
First, let's look at the first integral separately:
Some time ago I thought: “Hey, I haven’t completely forgotten the matan! Let me take this integral as indefinite, and then I will substitute the limits. Surely a couple of times in parts, and it's in the bag. Right now on a piece of paper I will decide everything without help. ” I want to warn you: do not repeat my mistakes. A sleepless night is waiting for you, and then you look in the directory and find out that the indefinite integral is not taken in elementary functions. For him, even a special function introduced.
However, with these specific limits, the integral can be taken in different ways. We will go the way that requires a minimum of basic knowledge (the most severe - the same integration in parts). To begin with, we will make a sudden replacement:
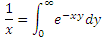
You ask: where did it all come from and why do we need another integral, which is not enough? Calmly, so necessary (familiar with the properties of the Laplace transformation fun grin). Substitute the replacement in the original formula and change the order of integration:
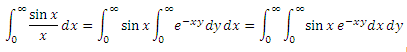
Inside it turned out to be an almost classical integral over dx , with which everyone was frightened in our physics school. It can also be taken as indefinite, twice using the integration formula in parts. Then on the right you will get some kind of murkiness and once again the same integral multiplied by something, and as a result you can solve the equation for this integral and get an answer, and then substitute the limits. Who cares, do it yourself, and I will idly write down the finished result:
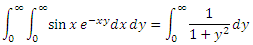
Well, now everything is quite simple: it is a table integral of high school, which is equal to arctangent. In infinity pi to half, in zero - zero, so we got the answer.
The integral, by the way, is so good that it has its own name - the Dirichlet integral . Under the link you can find other ways to take it.
')
For the next trip, we will need four things: a rectangular function, a cosine Fourier transform, a convolution, and the Parseval theorem. First I will say a few words about these wonderful things.
The rectangular function is that we will have such a step around zero:
The value 1/2 at the points of discontinuity is mainly needed to comply with the properties of the Fourier transform, in general it is not fundamental for our task.
Cosine Fourier transform . For simplicity, we digress a little from mathematical accuracy and formulate coarsely. For a sufficiently good even function f (x), the following relations hold:
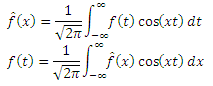
Function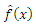
and is called the cosine Fourier transform (FCT) of f (x) (it is also called the image f). That is, the cosine transform of the cosine transform gives the original function f (x) again!
People familiar with signal processing are well aware that FCT from a rectangular function is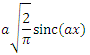
. It is easy to prove, using the above formulas and school knowledge. Since the rectangular function outside the interval [-a, a] is zero, you can simply integrate cos (xt) dt over this interval, there is a simple replacement of the variable and a table integral. The above property says that FCT from 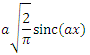- This is a rectangular function.
Convolution is another beautiful thing, without which signal processing can not do. For two functions f 1 (x) and f 2 (x), you can define a convolution function (indicated by an asterisk) like this:
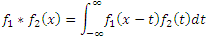
The convolution has a wonderful property for which it is loved: the Fourier transform turns it into multiplication, and the multiplication into convolution. More specifically, the cosine transform of the product of two good even functions is a convolution of their images divided by the root of two pi:
.
Parseval's theorem is a very cool statement about the equality of signal energy and its spectrum, which is written differently for different purposes. We need this version: for even and fairly good functions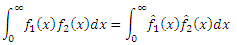
.
Take the second integral of our wonderful sequence. As many have already guessed, we will use Parseval's theorem and replace the multipliers with their FCT images:
The first rectangular function under the integral is equal to one for arguments less than one and zero for arguments to more than one. Therefore, nothing prevents us from removing it from the integral, adjusting the limits of integration:
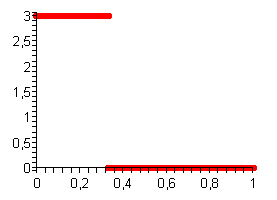
Under the integral there is a step of height 3 and width 1/3. Even a third-grader will take such an integral: you just need to multiply 3 and 1/3. The unit of the integral remains, and we have the pi we need! Thus, we almost honestly took the second integral from the series. Whoever wants to do this quite honestly, he will have to figure out what is the goodness of the function and prove that our functions are good.
To further it was easier, we denote this step under the integral as F 1 (x) and draw its graph:
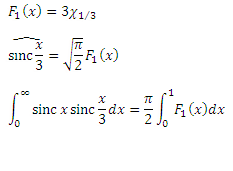
Let's go have fun further and look at the integral with three factors. To apply the Parseval theorem, we will now consider all factors from the second as one factor:
. With the image of the first factor, everything is already clear, and the image of the second factor is expressed through convolution:
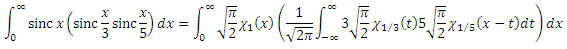
At first glance, scary. But it is possible to raise something, shorten something and substitute our F 1 (x) . Then we get:
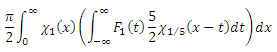
The internal integral is just a rectangular filter, a kind of “blur” for the function F 1 (x) : we simply average all values for plus and minus one-fifth for each point. Again, you can get rid of the rectangular function by shuffling the limits of integration. And with the external integral we will do the same procedure. Here is the result:
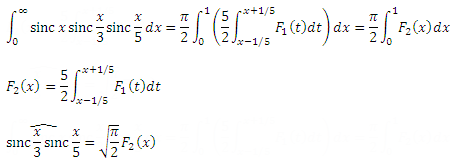
On the left is a graph of the function F 2 (x) , which is actually a smoothed F 1 (x) . It is easy to prove that after smoothing the function over the normalized kernel its integral does not change. Well, actually, we are talking about the integral from -∞ to + ∞, but for an even function this is true for the integral from zero. In this case, the core was a step from -1/5 to +1/5, multiplied by 5/2. The area under the step is one, which means that the core is normalized. Here, too, can be compared with the blur in Photoshop: after applying the blur, the picture as a whole does not become lighter or darker. And if so, then the integral F 2 (x) is exactly equal to the integral F 1 (x) , that is, one, therefore the third integral is equal to pi-half!
Further, the procedure is largely similar. The fourth integral is grouped as follows: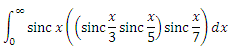
. First, Parseval's theorem, for convolution brackets, and we already know how to express the image of the inner bracket in F 2 (x) . Then everything is the same as last time, and as a result we get:
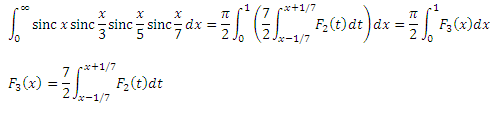
Now we already have F 3 (x) , which in reality is a smooth F 2 (x) with a kernel 2/7 wide. The kernel is normalized, so the integral F 3 (x) is equal to the integral F 2 (x) , that is, one, and again we have pi-half!
Great, we now click these integrals like nuts. But in theory, if it goes on like this, will they all be infinitely pi equal in half? Let's look further. Fifth integral:
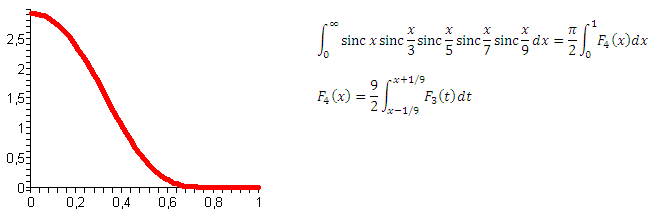
It seems all the same. All right, the sixth integral:
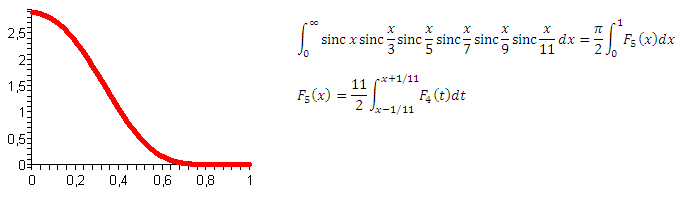
And there are no problems. Well, we take the seventh:
Nothing new! Okay, and the eighth?
Stop stop stop! Here we can not do without the team CSI!
The function has leaked through the unit! The integral F 7 (x) is still equal to unity, but if we integrate it from 0 to ∞. And we integrate to the unit! Until now, all functions were zero with x greater than one, but sooner or later it should have ended.
And how to understand when the end comes? It is very simple. F 1 (x) was non-zero at x <1/3. F 2 (x) smoothed it over ± 1/5, which means it was non-zero at x <1/3 + 1/5. Similarly, it is possible to find the boundary of nonzero values for all these functions, and for F 7 (x) this boundary for the first time exceeds unity:
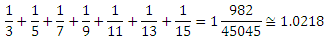
It is easy to even calculate how much specifically leaked, and thereby calculate the exact value of the eighth integral. Note that to the left of the boundary, F 1 (x) is a constant 3. F 2 (x) is a minus integral of this constant with a factor of 5/2, that is, a straight line with a factor of 3 × 5/2. F 3 (x) in sufficient proximity to the boundary 1/3 + 1/5 + 1/7 is the integral of that line with a factor of 7/2, that is, something like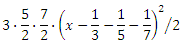
. Continuing the similar reasoning, we obtain the formula for F 7 (x) in the vicinity of the boundary:
Actually, the usual parabola of the sixth degree, shifted and multiplied. If we integrate it from one to the border 1/3 + 1/5 + 1/7 + 1/9 + 1/11 + 1/13 + 1/15, then we will find out how much function has flowed beyond the limits of the unit. You can solve this problem entirely in ordinary fractions. It turns out that's how much:
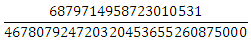
If this number is subtracted from one and multiplied by pi-halves, we get the final value of the eighth integral:
Such integrals are called the bornwein integrals in honor of David and Jonathan Borwein, who described them. If you want rigorous mathematical proofs (without any “good functions”) and other properties of these remarkable integrals, read the article of the authors .
Having opened these integrals, Jonathan Borwein introduced them into the Maple software package and, having made sure that Maple correctly took all eight integrals, informed the developers about the "bug": they say, the eighth integral should also be pi-halved, and you get what. Three days and three nights, he was killed by Jacques Caret , one of the Maple developers, in search of a mistake, until he realized that he was being cruelly joking. And they also say that mathematicians are boring people!
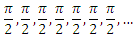
This obvious correct answer was suggested:
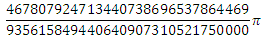
For those to whom it is not obvious how it was received, an explanation was offered. Let be
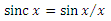(well, 1 for x = 0, although it does not matter). Then each member of the series is the value of the following integral in the chain: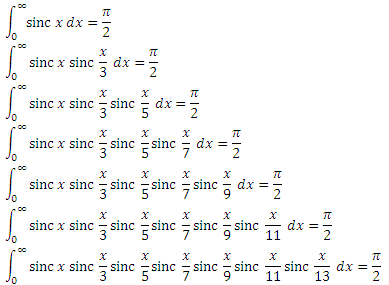So far everything is going well, but then suddenly:
In principle, this is enough to amuse fellow mathematicians, but I wanted to know how such integrals are generally considered and why such a ridiculous result is obtained. If someone else wants to shake the old days and remember the matan with the function, please read on.
The tale begins to affect
First, let's look at the first integral separately:
Some time ago I thought: “Hey, I haven’t completely forgotten the matan! Let me take this integral as indefinite, and then I will substitute the limits. Surely a couple of times in parts, and it's in the bag. Right now on a piece of paper I will decide everything without help. ” I want to warn you: do not repeat my mistakes. A sleepless night is waiting for you, and then you look in the directory and find out that the indefinite integral is not taken in elementary functions. For him, even a special function introduced.
However, with these specific limits, the integral can be taken in different ways. We will go the way that requires a minimum of basic knowledge (the most severe - the same integration in parts). To begin with, we will make a sudden replacement:
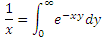
You ask: where did it all come from and why do we need another integral, which is not enough? Calmly, so necessary (familiar with the properties of the Laplace transformation fun grin). Substitute the replacement in the original formula and change the order of integration:
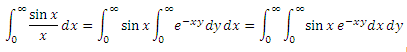
Inside it turned out to be an almost classical integral over dx , with which everyone was frightened in our physics school. It can also be taken as indefinite, twice using the integration formula in parts. Then on the right you will get some kind of murkiness and once again the same integral multiplied by something, and as a result you can solve the equation for this integral and get an answer, and then substitute the limits. Who cares, do it yourself, and I will idly write down the finished result:
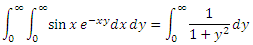
Well, now everything is quite simple: it is a table integral of high school, which is equal to arctangent. In infinity pi to half, in zero - zero, so we got the answer.
The integral, by the way, is so good that it has its own name - the Dirichlet integral . Under the link you can find other ways to take it.
')
Soon the tale is affected, and not soon the work is done
For the next trip, we will need four things: a rectangular function, a cosine Fourier transform, a convolution, and the Parseval theorem. First I will say a few words about these wonderful things.
The rectangular function is that we will have such a step around zero:
The value 1/2 at the points of discontinuity is mainly needed to comply with the properties of the Fourier transform, in general it is not fundamental for our task.
Cosine Fourier transform . For simplicity, we digress a little from mathematical accuracy and formulate coarsely. For a sufficiently good even function f (x), the following relations hold:
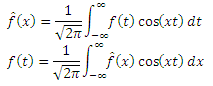
Function
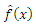and is called the cosine Fourier transform (FCT) of f (x) (it is also called the image f). That is, the cosine transform of the cosine transform gives the original function f (x) again!People familiar with signal processing are well aware that FCT from a rectangular function is
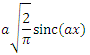. It is easy to prove, using the above formulas and school knowledge. Since the rectangular function outside the interval [-a, a] is zero, you can simply integrate cos (xt) dt over this interval, there is a simple replacement of the variable and a table integral. The above property says that FCT from 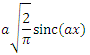- This is a rectangular function.Convolution is another beautiful thing, without which signal processing can not do. For two functions f 1 (x) and f 2 (x), you can define a convolution function (indicated by an asterisk) like this:
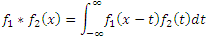
The convolution has a wonderful property for which it is loved: the Fourier transform turns it into multiplication, and the multiplication into convolution. More specifically, the cosine transform of the product of two good even functions is a convolution of their images divided by the root of two pi:
.Parseval's theorem is a very cool statement about the equality of signal energy and its spectrum, which is written differently for different purposes. We need this version: for even and fairly good functions
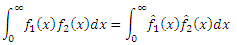.Dosselev Makar digging kitchen gardens, but now Makar got into the governor
Take the second integral of our wonderful sequence. As many have already guessed, we will use Parseval's theorem and replace the multipliers with their FCT images:
The first rectangular function under the integral is equal to one for arguments less than one and zero for arguments to more than one. Therefore, nothing prevents us from removing it from the integral, adjusting the limits of integration:
Under the integral there is a step of height 3 and width 1/3. Even a third-grader will take such an integral: you just need to multiply 3 and 1/3. The unit of the integral remains, and we have the pi we need! Thus, we almost honestly took the second integral from the series. Whoever wants to do this quite honestly, he will have to figure out what is the goodness of the function and prove that our functions are good.
To further it was easier, we denote this step under the integral as F 1 (x) and draw its graph:
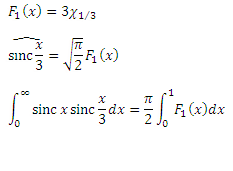
Let's go have fun further and look at the integral with three factors. To apply the Parseval theorem, we will now consider all factors from the second as one factor:
. With the image of the first factor, everything is already clear, and the image of the second factor is expressed through convolution: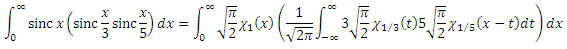At first glance, scary. But it is possible to raise something, shorten something and substitute our F 1 (x) . Then we get:
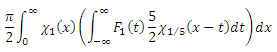
The internal integral is just a rectangular filter, a kind of “blur” for the function F 1 (x) : we simply average all values for plus and minus one-fifth for each point. Again, you can get rid of the rectangular function by shuffling the limits of integration. And with the external integral we will do the same procedure. Here is the result:
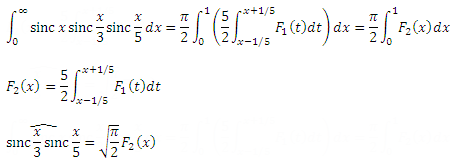
On the left is a graph of the function F 2 (x) , which is actually a smoothed F 1 (x) . It is easy to prove that after smoothing the function over the normalized kernel its integral does not change. Well, actually, we are talking about the integral from -∞ to + ∞, but for an even function this is true for the integral from zero. In this case, the core was a step from -1/5 to +1/5, multiplied by 5/2. The area under the step is one, which means that the core is normalized. Here, too, can be compared with the blur in Photoshop: after applying the blur, the picture as a whole does not become lighter or darker. And if so, then the integral F 2 (x) is exactly equal to the integral F 1 (x) , that is, one, therefore the third integral is equal to pi-half!
Further, the procedure is largely similar. The fourth integral is grouped as follows:
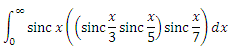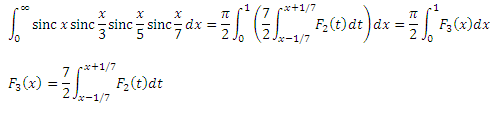
. First, Parseval's theorem, for convolution brackets, and we already know how to express the image of the inner bracket in F 2 (x) . Then everything is the same as last time, and as a result we get:Now we already have F 3 (x) , which in reality is a smooth F 2 (x) with a kernel 2/7 wide. The kernel is normalized, so the integral F 3 (x) is equal to the integral F 2 (x) , that is, one, and again we have pi-half!
Great, we now click these integrals like nuts. But in theory, if it goes on like this, will they all be infinitely pi equal in half? Let's look further. Fifth integral:
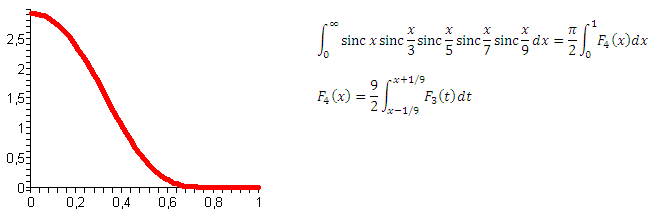
It seems all the same. All right, the sixth integral:
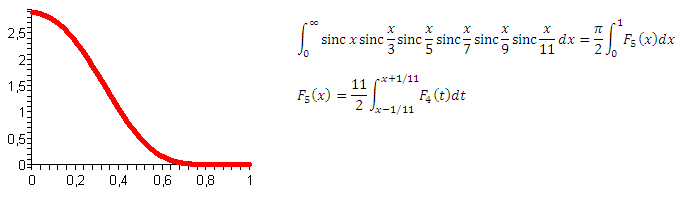
And there are no problems. Well, we take the seventh:
Nothing new! Okay, and the eighth?
Stop stop stop! Here we can not do without the team CSI!
The function has leaked through the unit! The integral F 7 (x) is still equal to unity, but if we integrate it from 0 to ∞. And we integrate to the unit! Until now, all functions were zero with x greater than one, but sooner or later it should have ended.
And how to understand when the end comes? It is very simple. F 1 (x) was non-zero at x <1/3. F 2 (x) smoothed it over ± 1/5, which means it was non-zero at x <1/3 + 1/5. Similarly, it is possible to find the boundary of nonzero values for all these functions, and for F 7 (x) this boundary for the first time exceeds unity:
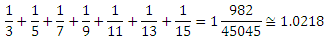
It is easy to even calculate how much specifically leaked, and thereby calculate the exact value of the eighth integral. Note that to the left of the boundary, F 1 (x) is a constant 3. F 2 (x) is a minus integral of this constant with a factor of 5/2, that is, a straight line with a factor of 3 × 5/2. F 3 (x) in sufficient proximity to the boundary 1/3 + 1/5 + 1/7 is the integral of that line with a factor of 7/2, that is, something like
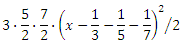. Continuing the similar reasoning, we obtain the formula for F 7 (x) in the vicinity of the boundary:Actually, the usual parabola of the sixth degree, shifted and multiplied. If we integrate it from one to the border 1/3 + 1/5 + 1/7 + 1/9 + 1/11 + 1/13 + 1/15, then we will find out how much function has flowed beyond the limits of the unit. You can solve this problem entirely in ordinary fractions. It turns out that's how much:
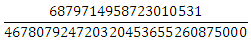
If this number is subtracted from one and multiplied by pi-halves, we get the final value of the eighth integral:
Such integrals are called the bornwein integrals in honor of David and Jonathan Borwein, who described them. If you want rigorous mathematical proofs (without any “good functions”) and other properties of these remarkable integrals, read the article of the authors .
Conclusion: eighty-level trolling
Having opened these integrals, Jonathan Borwein introduced them into the Maple software package and, having made sure that Maple correctly took all eight integrals, informed the developers about the "bug": they say, the eighth integral should also be pi-halved, and you get what. Three days and three nights, he was killed by Jacques Caret , one of the Maple developers, in search of a mistake, until he realized that he was being cruelly joking. And they also say that mathematicians are boring people!
Source: https://habr.com/ru/post/146140/
All Articles