This article is intended to clarify the essence of the fundamental methods of building and optimizing "artificial intelligence" for computer games (mostly antagonistic ). On the example of the game of hare and wolves, the Minimax algorithm and the Alpha Beta Clipping algorithm will be considered. In addition to the text description, the article contains illustrations, tables, sources, and a ready-made cross-platform game with open source, in which you can compete with an intelligent agent.

Game "Hare and wolves"

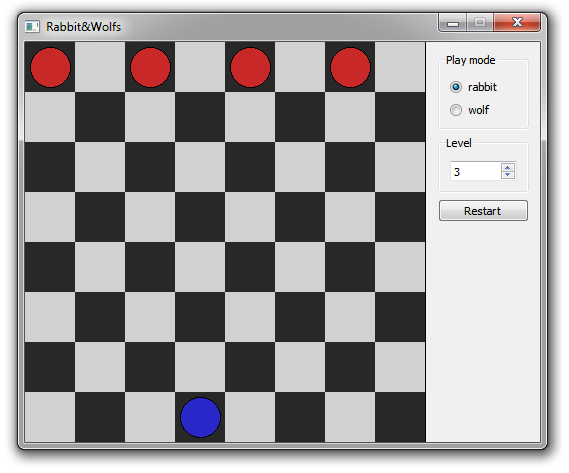
On the chessboard there are 4 wolves on top (on the black squares), and 1 hare on the bottom (on one of the black ones). The hare goes first. You can walk only one space diagonally, besides, wolves can only walk down, and the hare in any direction. The hare wins when it has reached one of the upper cages, and the wolves, when they have surrounded or pressed the hare (when the hare has nowhere to go).

Before continuing to read, I recommend to play , it will be easier to understand.

Heuristic

In practical engineering understanding, the minimax method relies on heuristics , which we will consider before proceeding to the essence of the algorithms.

In the context of a minimax, heuristics are needed to estimate the probability of a player’s victory, for a particular state. The task is to build a heuristic evaluation function , which is sufficiently quickly and accurately, in the selected metric, can indicate an estimate of the probability of a particular player's victory for a particular location of the figures, not relying on how the players came to this state. In my example, the evaluation function returns values ​​from 0 to 254, where 0 is the victory of the hare, 254 is the victory of the wolf, intermediate values ​​are the interpolation of the two estimates above. Estimation of probability is not a probability, and does not have to be limited, linear, continuous.

An example of the evaluation function 1 . The higher the hare, the greater his chances of winning. Such heuristics are effective in terms of speed (O (1)), but they are completely algorithmically unsuitable. The “height” of the hare correlates with the probability of victory, but it distorts the main goal of the hare — to win. This evaluation function tells the hare to move up, but with a small depth of calculation it will cause the hare to move up, regardless of obstacles, and fall into traps.

An example of the evaluation function 2 . The hare is more likely to win, the less he needs to make moves to win, with frozen wolves. This is a more cumbersome algorithm with complexity O (n), where n is the number of cells. Calculating the number of moves is reduced to the search in width:


Attention. The sources in the article are modified in such a way that the reader can understand their essence outside the context of the main application. Look for reliable sources at the end of the article.

The code that performs the search in width, or rather filling the map with values ​​equal to the “distance” from the hare:

this->queue.enqueue(this->rabbitPosition); while (!this->queue.empty()) { QPoint pos = this->queue.dequeue(); for (int i = 0; i < 4; i++) if (canMove(pos + this->possibleMoves[i])) { QPoint n = pos + this->possibleMoves[i]; this->map[ny()][nx()] = this->map[pos.y()][pos.x()] + 1; this->queue.enqueue(n); } } 

The result of the evaluation function should be a value equal to the “distance” to the nearest upper cell, or 254, if it is impossible to reach them. Despite the shortcomings that I will describe below, it is this heuristics used in the game.

For those who will look at the source and understand - attention! The application architecture is designed so that the evaluation function can be redone without affecting other parts of the code. But, you should use the previously selected metric, otherwise the algorithms will not understand the indications of the evaluation function.

Minimax

We introduce some concepts and notation:

• The state, it is the node of the decision tree - the location of the pieces on the board
• Terminal state is a state from which there are no more moves (someone won / draw).
  
• Vi is the i state.
• Vik is the k -th state, which can be reached in one move from the Vi state. In the context of a decision tree, this is a child node of Vi.
• f (Vi) is a calculated estimate of the probability of victory for the state Vi.
• g (Vi) is the heuristic estimate of the probability of victory for the state Vi.

f (Vi) differs from g (Vi) in that g (Vi) uses information only about Vi , and f (Vi) also uses Vik and other states, recursively.

The method is designed to solve the problem of choosing a move from the Vi state It is logical to choose a move for which the probability estimate will be the most profitable for the player who walks. In our metric, for wolves - the maximum score for the hares minimum. And the score is considered as follows:

• f (Vi) = g (Vi) , if Vi is a terminal state, or the depth limit of the calculations is reached.
• f (Vi) = max (f (Vi1), f (Vi2) ... f (Vik)) , if Vi is the state from which the player goes with the search for the maximum score.
• f (Vi) = min (f (Vi1), f (Vi2) ... f (Vik)) , if Vi is the state from which the player goes with the search for the minimum score.

The method relies on common sense. We go in such a way as to maximize our own victory P’s estimate, but in order to calculate at least something, we need to know how the enemy will walk, and the enemy will walk so as to maximize his victory score (minimize the P score). In other words, we know how the enemy will walk, and thus we can build estimates of probabilities. It's time to point out that the algorithm is optimal if the enemy has the same evaluation function, and it acts optimally. In this case, intelligence depends on the depth of the calculation, and on the quality of the evaluation function.

It's time to give an example:


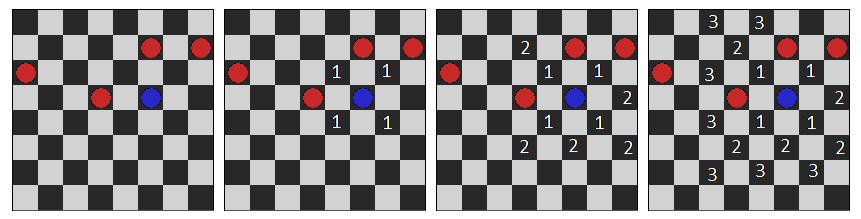
In this example, the player plays the hare, and the computer wolves. After the hare was like, the computer starts the minimax algorithm, in this example with a depth of 1. What does the algorithm do? Who knows? The algorithm goes through all possible moves for a wolf, and for them it gets an estimate of the probability of victory. This estimate, as we said earlier, consists of the same launch of the minimax algorithm, but for other states, and with the move of another player, and with minimization, instead of maximization. This will already be the second level, the last one for the specified depth 1, and the minimax algorithm does not start any further, but returns the heuristic evaluation function.

This example will be easier to understand if viewed from below. At the second level, we have states for which we get a heuristic estimate (it is written down by numbers). For the second level, the first one gets its estimates, respectively, by choosing the minimum values ​​from those that are checked at the next level. Well, the zero level, selects the maximum grade, from those that are provided to him by the first level.

Now that we have all the grades, what to do? Rejoice. Need to choose a move. Everything is obvious here; for a wolf, the move that shows the highest estimate chooses, for the hare, the move that shows the smallest. But after all, the estimates for different moves can be equal, and then ideally you need to choose randomly, but then the nuances begin. I’ll say right away that for me the first move from the list with the maximum rating is taken for the wolf, and the last of the list with the minimum rating for the wolf. And this is sad, since a rather serious optimization relies on the fact that the first move will always be selected from the desired list. But for a hare it does not fit. The fact is that the wolf very often (as far as possible) moves so that the estimate is equal to infinity (254), which makes any move of the hare “meaningless”, and if he chooses any move, he will walk down or whatever , and we need to make him go up, breaking through the front of the wolves. It would be correct to make the heuristic function take into account how high the hare is, but with a lower coefficient than the main heuristics, but I did not do it, but as I described earlier. Therefore, the last move from the list is selected, which indicates the hare to go up.

An example implementation of the algorithm:

  //    f(Vi) int Game::runMinMax(MonsterType monster, int recursiveLevel) { int test = NOT_INITIALIZED; //    ( )     if (recursiveLevel >= this->AILevel * 2) return getHeuristicEvaluation(); //  . 0-7 -   , 8-11 -    int bestMove = NOT_INITIALIZED; bool isWolf = (monster == MT_WOLF); int MinMax = isWolf ? MIN_VALUE : MAX_VALUE; //      for (int i = (isWolf ? 0 : 8); i < (isWolf ? 8 : 12); i++) { int curMonster = isWolf ? i / 2 + 1 : 0; QPoint curMonsterPos = curMonster == 0 ? rabbit : wolfs[curMonster - 1]; QPoint curMove = possibleMoves[isWolf ? i % 2 : i % 4]; if (canMove(curMonsterPos + curMove)) { //...,     temporaryMonsterMovement(curMonster, curMove); //,   ,    test = runMinMax(isWolf ? MT_RABBIT : MT_WOLF, recursiveLevel + 1); //   ,     - ,    if ((test > MinMax && monster == MT_WOLF) || (test <= MinMax && monster == MT_RABBIT)) { MinMax = test; bestMove = i; } //...     temporaryMonsterMovement(curMonster, -curMove); } } if (bestMove == NOT_INITIALIZED) return getHeuristicEvaluation(); //  , ,      if (recursiveLevel == 0 && bestMove != NOT_INITIALIZED) { if (monster == MT_WOLF) wolfs[bestMove / 2] += possibleMoves[bestMove % 2]; else rabbit += possibleMoves[bestMove % 4]; } return MinMax; } 

Attention! Here the variable bestMove encapsulates a lot of sense (I’ll clarify it when prompted), I urge you never to invest so much sense in 4 bits, if you are not sure that you are doing everything right.

Being literate and educated people, you have already guessed that where there are decision trees, there is also a treasure for optimizations. This example is no exception.

Alpha beta clipping

The alpha-beta pruning is based on the idea that the analysis of some moves can be stopped early, ignoring the result of their testimony. Alpha-beta pruning is often described as a separate algorithm, but I find it invalid and will describe it as an optimizing modification. Alpha-beta belongs to the class of branch and bound methods.

Roughly speaking, optimization introduces two additional variables, alpha and beta , where alpha is the current maximum value, less than which the maximization player (wolves) will never choose, and beta - the current minimum value, more than which the minimization player (hare) will never choose. Initially, they are set to -∞, + ∞, respectively, and as the estimates of f (Vi) are obtained, they are modified:

• alpha = max (alpha, f (Vi)); for the level of maximization.
• beta = min (beta, f (Vi)); for minimization level.

As soon as the condition alpha> beta becomes true, which means a conflict of expectations, we interrupt the analysis of Vik and return the last estimate of this level.

In our example, in the second figure, with the help of alpha-beta clipping, the 3 lower rows are completely truncated, but without the leftmost column. I believe that this is not a good example for an explanation, and therefore I will take an example from Wikipedia, which is a little more successful.


Legend in the example:

• Vi are the nodes of the decision search tree; i in no way correlates with the tree traversal order.
• Vi [alpha, beta] - nodes with the indicated current values ​​of alpha, beta.
• Ci is the i-th alpha-beta clipping.
• MIN, MAX - levels of maximization and minimization, respectively. Be careful, the states at the maximum level will choose their maxima from the states of the next level, where MIN is indicated, and vice versa. That is, the maximum is chosen from those on which MIN is written, and the minimum of those on which MAX is written, do not confuse.

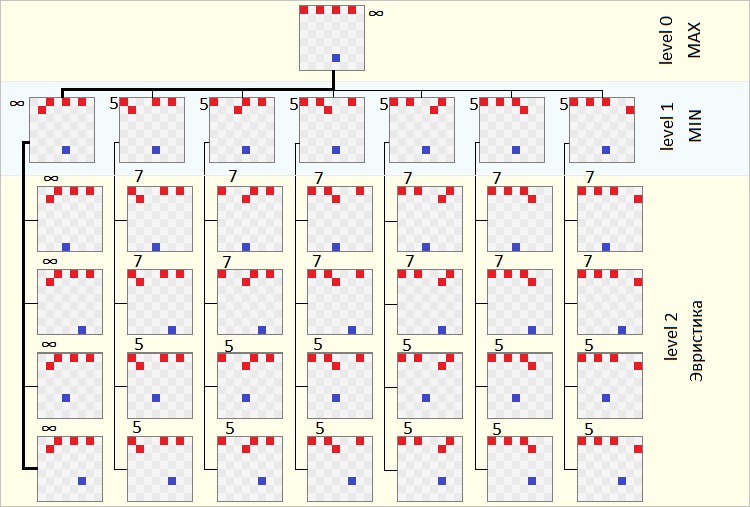
Consider clipping 1. After the variant with node V3 has been fully processed for node V1, and its estimate is f (V3) = 6, the algorithm refines the value of alpha for this node (V1) and passes its value to the next node - V4 . Now, for all child nodes of V4, the minimum alpha = 6. After the node V4 has processed the variant with node V5, and obtained the estimate f (V5) = 5, the algorithm refines the value beta for the node V4. After the update, for the V4 node we got a situation in which alpha> beta, and therefore no other variants of the V4 node need be considered. And it does not matter to us what grade the cut-off node will have:

• If the value of the clipped node is less than or equal to 5 (beta), then an estimate that is no more than 5 will be selected in node V4, and accordingly the option with node V4 will never be selected by node V1, because the estimate of node V3 is better.
• If the value of the cut-off node is greater than or equal to 6 (beta + 1), then the node will not be considered all the more, since the V4 node will choose the variant with the V5 node, since its estimate is lower (better).

Cut-off 2 is absolutely identical in structure, and I would recommend that you try to disassemble it yourself. Cut-off 3 is much more interesting, the attention , the example on Wikipedia is clearly somewhat wrong. He allows himself to cut off if (alpha> = beta), although alpha-beta should be an optimization, and not influence the choice of the path. The fact is that everywhere they write that clipping should work when alpha> = beta, although in the general case, only when alpha> beta.

Suppose for some decision tree, all children show the same score. Then you could choose any of them, randomly, and that would be correct. But you will not be able to do so, using the conditions alpha> = beta, because after the first assessment all the others can be cut off. But it doesn't matter, for example, your algorithm will not implement stochastic behavior, it is not so important, but if in your algorithm the choice of the best of the values ​​with the same rating is important, then such a cut-off condition will result in the algorithm simply failing and going not optimal. Be carefull!

Alpha-beta pruning is a very simple algorithm to implement, and its essence is that you need to add 2 alpha and beta variables to the minimax function in the interface of the minimax procedure, and a small piece of code into its body immediately after receiving the estimate.

An example of a modification of the minimax algorithm with alpha-beta clipping (for greater clarity, the modifications made are commented out, but remember that this is an important code, not comments):

 int Game::runMinMax(MonsterType monster, int recursiveLevel/*, int alpha, int beta*/) { int test = NOT_INITIALIZED; if (recursiveLevel >= this->AILevel * 2) return getHeuristicEvaluation(); int bestMove = NOT_INITIALIZED; bool isWolf = (monster == MT_WOLF); int MinMax = isWolf ? MIN_VALUE : MAX_VALUE; for (int i = (isWolf ? 0 : 8); i < (isWolf ? 8 : 12); i++) { int curMonster = isWolf ? i / 2 + 1 : 0; QPoint curMonsterPos = curMonster == 0 ? this->rabbit : this->wolfs[curMonster - 1]; QPoint curMove = this->possibleMoves[isWolf ? i % 2 : i % 4]; if (canMove(curMonsterPos + curMove)) { temporaryMonsterMovement(curMonster, curMove); test = runMinMax(isWolf ? MT_RABBIT : MT_WOLF, recursiveLevel + 1, alpha, beta); temporaryMonsterMovement(curMonster, -curMove); if ((test > MinMax && monster == MT_WOLF) || (test <= MinMax && monster == MT_RABBIT)) { MinMax = test; bestMove = i; } /* if (isWolf) alpha = qMax(alpha, test); else beta = qMin(beta, test); if (beta < alpha) break; */ } } if (bestMove == NOT_INITIALIZED) return getHeuristicEvaluation(); if (recursiveLevel == 0 && bestMove != NOT_INITIALIZED) { if (monster == MT_WOLF) this->wolfs[bestMove / 2] += this->possibleMoves[bestMove % 2]; else this->rabbit += this->possibleMoves[bestMove % 4]; } return MinMax; } 

As I said earlier, alpha-beta clipping is very effective, and the following indicators are proof of this. For each case, at three different levels of calculation depth, I measured the number of entries in the heuristic evaluation function (less is better), and this is what happened:

As a conclusion, I can say that the use of this cut-off algorithm will not only speed up the work of the intellect, but will also increase its level.

Nuances

The algorithm makes optimal moves only if its opponent thinks optimally. The quality of the course mainly depends on the depth of the recursion, and on the quality of the heuristics. But it should be noted that this algorithm evaluates the quality of the course deep enough, and in no way is tied (if not explicitly prescribed somewhere in the heuristics) for the number of moves. In other words, if you apply this algorithm to chess, without additional modifications, it will put the mats later than it could. And in this example, if the hare realizes that he has no way to win, with the optimal strategy of the wolves, he can commit suicide, despite the fact that he could delay the loss.

Again, never make alpha-beta cut-off for alpha-beta, unless you are 100% sure that this is acceptable for your implementation. Otherwise, your alpha beta will degrade the intelligence of the algorithm as a whole, with a high probability.

The algorithm is fundamental, in the sense that it is the foundation for a large variety of different modifications. In the form in which it is presented here, it cannot be used for checkers, chess, go. Most modifications seek:

• Reuse calculations.
• Analyze different situations with different depths.
• Increase the number of cuts, due to the general principles and heuristics for a particular game.
• Introduce move patterns. For example, in chess, the first few moves are openings, not a minimax job.
• Introduce third-party quality measures moves. For example, to check whether it is possible to win in one move, and if it is possible to win, and not to launch the minimax.
• Much more.

A huge number of modifications and allow the computer to play chess, and even beat the person. Without such modifications, minimax is practically not applicable to chess, even on modern super computers. Without optimizations, in chess for three moves, it would be necessary to check about 30 ^ 6 moves (729 billion), but we need the depth of calculation to be more ...

Happy end

As promised - the source , the version for Windows (should work in vayne). I recommend trying to write the same thing for checkers, chess is useful.