Russian Code Cup 2012: Analysis of the tasks of the second qualifying round
Last Saturday, the second qualifying round of the Russian Code Cup 2012 programming contest was held.

The Russian Code Cup is an individual sports programming competition held annually by the Mail.Ru Group . It traditionally consists of three stages: at the beginning of the summer three qualifying rounds take place, then the best take part in the qualifying round, the first fifty winners of the qualifying round compete in the final. Personal presence will require only the last of them, the rest are held online. All finalists will be awarded with valuable gifts, and the prize for the participant who won first place will be $ 10,000. For the second and third place rely 5,000 and 3,000 dollars.
')
In this article, I will examine in detail the tasks submitted to the competition, as well as share the statistics of the round. I tried to clarify the details so that the solution of problems was understandable even to those who are still taking the first steps. Also, this material will help to get an idea of how difficult the tasks are offered at the qualifying stages of the Russian Code Cup programming championship.
This Sunday, June 10, at 11:00, the last qualifying round will be held, from which two hundred participants will go to the "semi-final" - the qualifying round. In the second round, it was enough to solve two problems - one simple and one difficult, and to meet the half of the allotted time. We are waiting for you on Sunday and good luck!
Well, now move on to the tasks.
- no more than 1 S and no more than 2 OC,
- no more than 2 S and no more than 1 OC.
In all other cases, “no” should have been output.
Full condition, see the site RussianCodeCup.ru
It probably does not make sense to analyze this problem in detail here - it is really very simple.
Here it is interesting that the solution of this problem recursively fits the definition of a simple task. One of its most elegant solutions is to check the sum of squares of the entered values: (OV * OV + OT * OT) <6.
A total of 1261 solutions were sent for verification, of which the correct 722 (57%). 77% of the participants of the Russian Code Cup coped with this task. The first decision came from Andrei Maxi 1 minute 37 seconds after the start of the round.
(N characters) string (M characters) actions (N characters),
for all cases where the prefix and suffix do not overlap with each other. An example when this is possible was demonstrated in the statement of the problem — then the suffix and prefix defined the same characters: ababc was an encrypted bab.
Full condition, see the site RussianCodeCup.ru
Obviously, to restore the string, you must find a sequence that has an exact mirror image. That is, the maximum continuous sequence of positions i, for which the condition s [i] = s [l - i - 1] is satisfied, constitutes the search string.
To do this, for each position i, we can calculate the value of k — the length of the largest substring s [i — k..i], in which all characters satisfy our condition. The values found are stored in an array, after which we find in it the position of the leftmost occurrence of the maximum value.
To calculate the length of the substring p [i], we will use the already calculated value of p [i — 1], this will greatly reduce the time and resources.
The answer is a substring of length p [max], ending in the character with the number max, where max is the position of the leftmost occurrence of the maximum value in the array p.
A total of 1,158 solutions were sent for verification, of which 337 were correct (29%). 36% of participants of the Russian Code Cup QR2 coped with this task. The first decision came from Kurtov Nikolay 9 minutes after the start of the round.
Full condition, see the site RussianCodeCup.ru
Let me remind you that a tetrahedron is a polyhedron whose faces are four triangles (in other words, a triangular pyramid).
It all starts with the fact that we iterate over possible matches of matches to the edges of a tetrahedron. Denote the desired tetrahedron as ABCD. It has six edges: AB, AC, AD, BC, BD and CD. Let's go through all 6! = 720 variants, which match corresponds to which edge. Now it remains to verify that the corresponding tetrahedron exists.
How to check the existence of a tetrahedron? There are at least three solutions.
The first solution is based on calculating the volume of a tetrahedron. The simplest solution is to find a formula for calculating the volume of a tetrahedron by faces. This task itself is not an easy one; I will give here a formula:
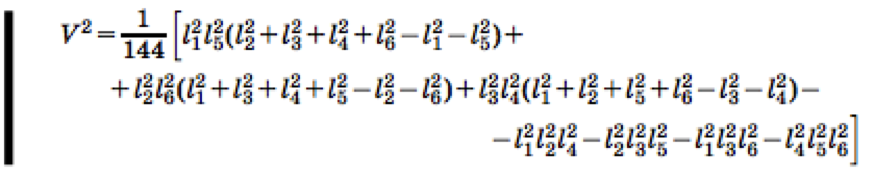
Accordingly, if the right-hand side of the equation turns out to be negative or the triangles in the faces cannot be constructed (the triangle inequality), then the tetrahedron will not converge.
For those interested - here this formula is displayed: http://www.mccme.ru/free-books/mmmf-lectures/book.21.pdf
The second approach to solving the problem is geometric. First, make sure that ABC and BCD exist. Now try to make a tetrahedron. It is clear that when building a volumetric figure, a problem can arise only with the last edge - it can be either too long or too short. Therefore, this solution proposes to find the range of the length of the last edge.
There are two limiting ways for placing faces in which the tetrahedron turns into a flat figure. The first is when the faces are rotated 180 degrees relative to each other (CAB and CBD), and the second is when they are “folded” and form a “zero angle” (CA'D and CDB). All admissible positions of faces relative to each other are in the range between these boundary ones. The last edge (AD) reaches its greatest length in the first limiting variant (AD), and the smallest - in the last (A'D). Consequently, a tetrahedron will exist if this length of the last edge fits into the range found by us (from A'D to AD).
In order to find the distance between points A and D and A 'and D, we first find their coordinates, taking one of the common vertices for the triangles as zero, and draw the abscissa axis through one of the edges emanating from this vertex. To find the coordinates of all the other vertices in this coordinate system is quite simple: we will determine the vertex positions in polar coordinates (angle, distance) through the aspect ratios and cosines of the angles, then we translate them into Cartesian coordinate systems. Knowing the coordinates of the vertices, it is quite simple to calculate the maximum and minimum distances between unbound vertices.
The program should check if the length of the remaining face fits into the specified ranges. If yes, then a tetrahedron of such lengths can be “assembled”.
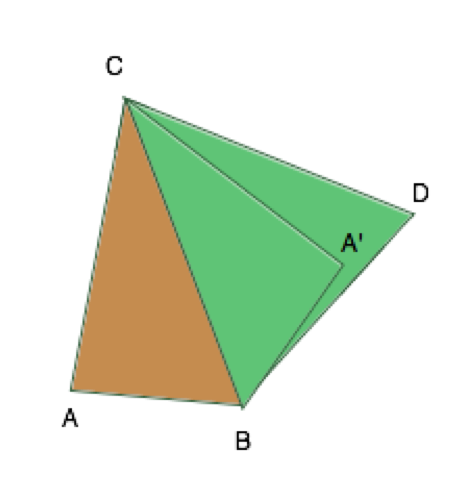
The third way is also geometric. First you need to check the existence of all triangles with the specified sides. If at least one triangle cannot be built on the indicated values of the sides, then a tetrahedron cannot be built either. For verification, it is necessary to verify the inequality of a non-degenerate triangle — each of its sides must be strictly less than the sum of the two others.
In many cases, this decision was limited; Meanwhile, there are situations when triangles with specified sides can be constructed, and a tetrahedron cannot be assembled from them.
For example, if we have faces (100,100,2,101,100,2), then the triangles (100,100,2) and (101,100,2) formally satisfy the triangle inequality, but the tetrahedron of these triangles cannot be folded. From the figure we see that the edge AC is almost parallel to AB, which means that the distance from D to C will almost not change at any inclination of the face ABD relative to AB, from which it can be concluded that DB is almost perpendicular to BC. In this case, the DC can be roughly estimated as the root of the sum of the squares of the legs, that is, the DC should be about 10, and not at all 2, as we assumed in the condition.

Therefore, in addition to checking for triangles in the edges, it is necessary to perform an additional check for triangular angles. There are two necessary and sufficient conditions for the existence of a triangular angle:
The plane angle is through the cosine theorem for the triangle.
In total, 1088 solutions were sent for verification, of which only 74 were correct (7%). 8% of participants of the Russian Code Cup QR2 coped with this task. The first decision came from a participant with the nickname AVictor 30 minutes after the start of the round.
Full condition, see the site RussianCodeCup.ru
The key solution in this problem is the choice of a dynamic programming method for subsets (masks). The method involves encoding the set through bit sequences for the convenience of further operations. It is easy to work with small sets through bit operations. In particular, the encoding of the theme set requires 18 bits. Then thei-th bit in the binary number will be responsible for whether the i-th theme is already taken (1), or not yet (0). As a result, all the sets of themes can be stored in the standard 32-bit whole. In total, there are 2 ^ 18 masks defining 2 ^ 18 subsets.
Storing subsets in bits is also convenient because the standard bit AND (AND) operations allow you to cross sets, and bit OR (OR) allows you to combine sets.
Since there is a constraint in the formulation of the problem, which requires that the task of each level of complexity be presented, we introduce another dimension, the dp [i] [j] array. It will determine whether it is possible, taking on the task from the first i levels of complexity, to type in a set of topics given by the bit mask j, without intersecting the topics between the tasks taken.
Then we go to the level above (i + 1), choosing among tasks of complexity i + 1 is the one, the bit mask of which does not intersect with the state mask, and so on until we reach the situation when all the topics are exhausted (right upper matrix angle). If such problems of complexity i + 1 could not be found, then the answer is Impossible.
A total of 407 solutions were sent to check, of which only 115 were correct (28%). 12% of participants of the Russian Code Cup QR2 coped with this task. The first decision came from Nikita Ioffe 16 minutes after the start of the round.
Full condition, see the site RussianCodeCup.ru
Despite the fairly simple formulation, this problem is the most difficult of the presented. Here the main difficulty is that the text size can be large, and using sequential scanning and direct counting is inefficient.
To solve the problem, the segment tree data structure is used. It allows you to quickly perform operations of changing any element to a new value and quickly calculate some functions (sum, minimum, maximum) on an arbitrary interval from i to j. “Fast” in this case means behind O (log n), that is, much faster than with sequential viewing.
The algorithm that implements the concept of a segment tree can be found here: e-maxx.ru/algo/segment_tree .
In our case, in the segment tree we will store the current “depth” of the bracket sequence for each position in the text. It will be stored in the leaves of the tree, the calculated minima will be stored in the tops, in the root of the tree - the absolute minimum throughout the tree.
Accordingly, the search for the closing bracket is reduced to the search for the element on the right (for the opening bracket) or on the left (for the closing bracket) having the same depth. Instead of sequential viewing, there will be a descent through the tree - by minima of values not exceeding the depth before the opening bracket or after the closing bracket.
When inserting a bracket, it is necessary to recalculate all elements to the right of it, as well as all the minima at the vertices covering these elements. Here so-called can be used. “Late” update - information about the change remains at the vertices and goes down to the “leaves” when you need to refer to them.
In total, 159 solutions were sent to check, of which only 8 were correct (5%). Less than 1% of the participants of the Russian Code Cup QR2 coped with this task. The first decision came from Sergey Fedorov 54 minutes after the start of the round.

The Russian Code Cup is an individual sports programming competition held annually by the Mail.Ru Group . It traditionally consists of three stages: at the beginning of the summer three qualifying rounds take place, then the best take part in the qualifying round, the first fifty winners of the qualifying round compete in the final. Personal presence will require only the last of them, the rest are held online. All finalists will be awarded with valuable gifts, and the prize for the participant who won first place will be $ 10,000. For the second and third place rely 5,000 and 3,000 dollars.
')
In this article, I will examine in detail the tasks submitted to the competition, as well as share the statistics of the round. I tried to clarify the details so that the solution of problems was understandable even to those who are still taking the first steps. Also, this material will help to get an idea of how difficult the tasks are offered at the qualifying stages of the Russian Code Cup programming championship.
This Sunday, June 10, at 11:00, the last qualifying round will be held, from which two hundred participants will go to the "semi-final" - the qualifying round. In the second round, it was enough to solve two problems - one simple and one difficult, and to meet the half of the allotted time. We are waiting for you on Sunday and good luck!
Well, now move on to the tasks.
"Simple Task"
Obviously, this task with “speaking” name and content was for warming up — it had to be solved quickly and on the first attempt. The participant's program should have answered whether the task is simple by checking the criteria for a simple task. At the input, the number of branch operators (OV) and cycle operators (OC) was given and it was necessary to output “yes” in one of two cases:- no more than 1 S and no more than 2 OC,
- no more than 2 S and no more than 1 OC.
In all other cases, “no” should have been output.
Full condition, see the site RussianCodeCup.ru
It probably does not make sense to analyze this problem in detail here - it is really very simple.
Here it is interesting that the solution of this problem recursively fits the definition of a simple task. One of its most elegant solutions is to check the sum of squares of the entered values: (OV * OV + OT * OT) <6.
A total of 1261 solutions were sent for verification, of which the correct 722 (57%). 77% of the participants of the Russian Code Cup coped with this task. The first decision came from Andrei Maxi 1 minute 37 seconds after the start of the round.
"Key"
This task is a little more difficult. By the condition of the problem, our string is mirrored relative to the center of the encrypted string, therefore, the cipher is the following construction:(N characters) string (M characters) actions (N characters),
for all cases where the prefix and suffix do not overlap with each other. An example when this is possible was demonstrated in the statement of the problem — then the suffix and prefix defined the same characters: ababc was an encrypted bab.
Full condition, see the site RussianCodeCup.ru
Obviously, to restore the string, you must find a sequence that has an exact mirror image. That is, the maximum continuous sequence of positions i, for which the condition s [i] = s [l - i - 1] is satisfied, constitutes the search string.
To do this, for each position i, we can calculate the value of k — the length of the largest substring s [i — k..i], in which all characters satisfy our condition. The values found are stored in an array, after which we find in it the position of the leftmost occurrence of the maximum value.
To calculate the length of the substring p [i], we will use the already calculated value of p [i — 1], this will greatly reduce the time and resources.
p [i] = 0 if s [i] <> s [l - i - 1] p [i] = 1 if i = 0 and s [0] = s [l —1] p [i] = p [i-1] + 1, if i> 0 and s [i] = s [l - i - 1]
| No | 0 | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Characters | c | x | b | a | y | d | z | a | b | x | e |
| c = e? | x = x? | b = b? | a = a? | y = z? | d = d? | z = y? | a = a? | b = b? | x = x? | e = c? | |
| not | Yes | Yes | Yes | not | Yes | not | Yes | Yes | Yes | not | |
| 0 | 0 + 1 = | 1 + 1 = | 2 + 1 = | 0 | 0 + 1 = | 0 | 0 + 1 = | 1 + 1 = | 2 + 1 = | 0 | |
| 0 | one | 2 | 3 | 0 | one | 0 | one | 2 | 3 | 0 | |
| 3 | 3 | 0 |
The answer is a substring of length p [max], ending in the character with the number max, where max is the position of the leftmost occurrence of the maximum value in the array p.
A total of 1,158 solutions were sent for verification, of which 337 were correct (29%). 36% of participants of the Russian Code Cup QR2 coped with this task. The first decision came from Kurtov Nikolay 9 minutes after the start of the round.
"Tetrahedron"
In the first qualification, the match problem was the simplest: it was necessary to calculate whether the parallelepiped could be folded from the specified set. Folding a tetrahedron from the same matches was not so easy - the first correct decision came 30 minutes after the start of the tournament.Full condition, see the site RussianCodeCup.ru
Let me remind you that a tetrahedron is a polyhedron whose faces are four triangles (in other words, a triangular pyramid).
It all starts with the fact that we iterate over possible matches of matches to the edges of a tetrahedron. Denote the desired tetrahedron as ABCD. It has six edges: AB, AC, AD, BC, BD and CD. Let's go through all 6! = 720 variants, which match corresponds to which edge. Now it remains to verify that the corresponding tetrahedron exists.
How to check the existence of a tetrahedron? There are at least three solutions.
The first solution is based on calculating the volume of a tetrahedron. The simplest solution is to find a formula for calculating the volume of a tetrahedron by faces. This task itself is not an easy one; I will give here a formula:
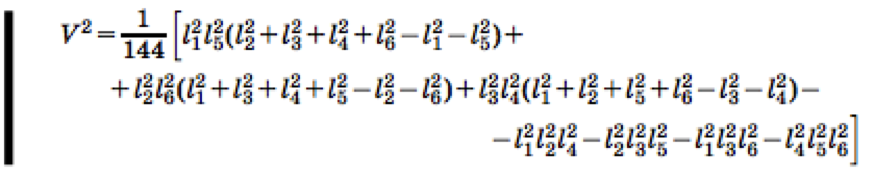
Accordingly, if the right-hand side of the equation turns out to be negative or the triangles in the faces cannot be constructed (the triangle inequality), then the tetrahedron will not converge.
For those interested - here this formula is displayed: http://www.mccme.ru/free-books/mmmf-lectures/book.21.pdf
The second approach to solving the problem is geometric. First, make sure that ABC and BCD exist. Now try to make a tetrahedron. It is clear that when building a volumetric figure, a problem can arise only with the last edge - it can be either too long or too short. Therefore, this solution proposes to find the range of the length of the last edge.
There are two limiting ways for placing faces in which the tetrahedron turns into a flat figure. The first is when the faces are rotated 180 degrees relative to each other (CAB and CBD), and the second is when they are “folded” and form a “zero angle” (CA'D and CDB). All admissible positions of faces relative to each other are in the range between these boundary ones. The last edge (AD) reaches its greatest length in the first limiting variant (AD), and the smallest - in the last (A'D). Consequently, a tetrahedron will exist if this length of the last edge fits into the range found by us (from A'D to AD).
In order to find the distance between points A and D and A 'and D, we first find their coordinates, taking one of the common vertices for the triangles as zero, and draw the abscissa axis through one of the edges emanating from this vertex. To find the coordinates of all the other vertices in this coordinate system is quite simple: we will determine the vertex positions in polar coordinates (angle, distance) through the aspect ratios and cosines of the angles, then we translate them into Cartesian coordinate systems. Knowing the coordinates of the vertices, it is quite simple to calculate the maximum and minimum distances between unbound vertices.
The program should check if the length of the remaining face fits into the specified ranges. If yes, then a tetrahedron of such lengths can be “assembled”.

The third way is also geometric. First you need to check the existence of all triangles with the specified sides. If at least one triangle cannot be built on the indicated values of the sides, then a tetrahedron cannot be built either. For verification, it is necessary to verify the inequality of a non-degenerate triangle — each of its sides must be strictly less than the sum of the two others.
In many cases, this decision was limited; Meanwhile, there are situations when triangles with specified sides can be constructed, and a tetrahedron cannot be assembled from them.
For example, if we have faces (100,100,2,101,100,2), then the triangles (100,100,2) and (101,100,2) formally satisfy the triangle inequality, but the tetrahedron of these triangles cannot be folded. From the figure we see that the edge AC is almost parallel to AB, which means that the distance from D to C will almost not change at any inclination of the face ABD relative to AB, from which it can be concluded that DB is almost perpendicular to BC. In this case, the DC can be roughly estimated as the root of the sum of the squares of the legs, that is, the DC should be about 10, and not at all 2, as we assumed in the condition.

Therefore, in addition to checking for triangles in the edges, it is necessary to perform an additional check for triangular angles. There are two necessary and sufficient conditions for the existence of a triangular angle:
- the sum of the flat corners of the triangular angle should be less than 360 degrees,
- each flat angle of the triangular angle should be less than the sum of the two other flat angles.
The plane angle is through the cosine theorem for the triangle.
In total, 1088 solutions were sent for verification, of which only 74 were correct (7%). 8% of participants of the Russian Code Cup QR2 coped with this task. The first decision came from a participant with the nickname AVictor 30 minutes after the start of the round.
"Tasks"
By the condition of the task, it was necessary to find a subset of competitive tasks for which the requirements would be fulfilled: 1) one task at each level of complexity, 2) each topic is presented, 3) no two tasks overlap by topic. The input data contained descriptions of the tasks: which set of topics corresponds to which tasks and the complexity of the tasks. At the output, it was necessary to display the required subset of tasks in the form of their indices (numbers) or to derive Impossible, if such a subset does not exist.Full condition, see the site RussianCodeCup.ru
The key solution in this problem is the choice of a dynamic programming method for subsets (masks). The method involves encoding the set through bit sequences for the convenience of further operations. It is easy to work with small sets through bit operations. In particular, the encoding of the theme set requires 18 bits. Then the
Storing subsets in bits is also convenient because the standard bit AND (AND) operations allow you to cross sets, and bit OR (OR) allows you to combine sets.
Since there is a constraint in the formulation of the problem, which requires that the task of each level of complexity be presented, we introduce another dimension, the dp [i] [j] array. It will determine whether it is possible, taking on the task from the first i levels of complexity, to type in a set of topics given by the bit mask j, without intersecting the topics between the tasks taken.
Then we go to the level above (i + 1), choosing among tasks of complexity i + 1 is the one, the bit mask of which does not intersect with the state mask, and so on until we reach the situation when all the topics are exhausted (right upper matrix angle). If such problems of complexity i + 1 could not be found, then the answer is Impossible.
for (int[] t : P) { Arrays.fill(t, -1);} // “-1” P[0][0] = -2; // for (int i = 0; i < tl.length; ++i) { // for (Task t : tl[i]) { // for (int mask = 0; mask < P[i].length; ++mask) { // if ((mask & t.mask) == 0 && P[i][mask] != -1) { // // dp[i + 1][mask | t.mask] = t.num; } } } } // if (dp[d][(1 << m) - 1] == -1) { out.println("Impossible"); // … } else { out.println("OK"); int[] ans = new int[d]; int mask = (1 << m) - 1; // for (int i = d; i > 0; --i) { ans[i - 1] = dp[i][mask] + 1; mask ^= mm[dp[i][mask]]; } for (int i : ans) { out.print(i + " "); } } A total of 407 solutions were sent to check, of which only 115 were correct (28%). 12% of participants of the Russian Code Cup QR2 coped with this task. The first decision came from Nikita Ioffe 16 minutes after the start of the round.
"Text editor"
In the input task, we get the position and the character (alphabetic + brackets) entered in this position, at the output - with each input of the bracket we must return the position of the previously entered pair bracket, or −1 if the pair bracket does not exist. It is necessary to correctly handle the situation that the input data can change one previously added bracket to another, as well as the fact that there can be a lot of characters and brackets (text size is 100000).Full condition, see the site RussianCodeCup.ru
Despite the fairly simple formulation, this problem is the most difficult of the presented. Here the main difficulty is that the text size can be large, and using sequential scanning and direct counting is inefficient.
To solve the problem, the segment tree data structure is used. It allows you to quickly perform operations of changing any element to a new value and quickly calculate some functions (sum, minimum, maximum) on an arbitrary interval from i to j. “Fast” in this case means behind O (log n), that is, much faster than with sequential viewing.
The algorithm that implements the concept of a segment tree can be found here: e-maxx.ru/algo/segment_tree .
In our case, in the segment tree we will store the current “depth” of the bracket sequence for each position in the text. It will be stored in the leaves of the tree, the calculated minima will be stored in the tops, in the root of the tree - the absolute minimum throughout the tree.
Accordingly, the search for the closing bracket is reduced to the search for the element on the right (for the opening bracket) or on the left (for the closing bracket) having the same depth. Instead of sequential viewing, there will be a descent through the tree - by minima of values not exceeding the depth before the opening bracket or after the closing bracket.
When inserting a bracket, it is necessary to recalculate all elements to the right of it, as well as all the minima at the vertices covering these elements. Here so-called can be used. “Late” update - information about the change remains at the vertices and goes down to the “leaves” when you need to refer to them.
In total, 159 solutions were sent to check, of which only 8 were correct (5%). Less than 1% of the participants of the Russian Code Cup QR2 coped with this task. The first decision came from Sergey Fedorov 54 minutes after the start of the round.
- Analysis of tasks from the first qualification
Analysis of tasks from the third qualification
Aliyev Rauf
Director of Research and Education
Project Manager Russian Code Cup
Mail.Ru Group
Source: https://habr.com/ru/post/145262/
All Articles