The algorithm of parallel search for maximum, common substrings in two lines, and its implementation in C ++ (C ++ 11)
I decided to write an article about the parallel search algorithm for the maximum possible intersection of two lines. By writing this article I was motivated by two wishes:
It all started with a competition held by Intel, which I learned from the post . The essence of the competition came down to the development and implementation of an algorithm that solves the problem of finding the common substring in two strings as long as possible (I think it makes no sense to rewrite the whole task here). The reference code was attached to the problem, i.e. decision on which it was necessary to "be equal". A little later, from the forum dedicated to this competition, it became clear that the reference code does not solve this problem in the form in which it is formulated on the Intel website. Those. the whole point of the competition was as follows: “to make a program that exactly repeats the output of the reference code, with the same input parameters, only so that it is faster and more parallel”.
Well, okay, even despite the absurdity of the situation with the description of the task, I immediately rejected participation in the competition also because only students and graduates could participate there. I liked the task itself, the one that is described on the site.
Here is how I understood from the description this task:
There are two strings S1 and S2 , you need to find the longest common substring (s) (hereafter, we will call the desired substrings - subsets), the length of which is not less than M. As a result, output its coordinates.
The coordinates are four integers.
The first two refer to the string S1 - the position numbers of the first and last characters of the found substring.
The second two numbers have the same meaning, only refer to the second line - S2 .
For example, if we have the following input parameters:
')
S1 = ABCCA
S2 = ACCABABCCBAABCBAABCBACBACBACBAC
M = 2
then the answer will be:
0 3 5 8
(in the original formulation of the problem, the coordinates need to be output starting from 1, but these are details of the result output, and they do not belong to the algorithm itself).
Also in the requirements for the task there is one more additional input parameter K - the number of threads that can be used to parallelize the algorithm.
Let us sum up what is given to us at the entrance:
In fact, the idea of the solution is very simple and consists of 3 steps:
Consider the operation of the algorithm in the following example:
S1 = ABCCA
S2 = ACCABABCCBAABCBAABCBACBACBACBAC
M = 2
K = 2
1) Split S1 into segments, each with a length of M = 2:
AB , BC , CC , CA
2) We project each resulting segment on S2 :

or in the form of offsets:

so we got the projection of S1 to S2 :

we will call this projection - the intersection map.
In fact, the intersection map is a matrix of coordinates of all segments whose length is equal to M. Those. each element of the matrix characterizes the coordinate in row S2 , while the row number of the matrix characterizes the coordinate in row S1 . Having the intersection map at our disposal, we can find all the intersections (subsets) and choose the maximum ones.
3) Search for maximum subsets (a set of segments).
If you look at the intersection map in symbolic form, you can already visually find the longest subset:
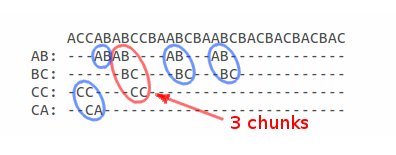
If we take into account that each segment can serve as the beginning of a subset, then using the intersection map, we can calculate the length of all subsets, the beginning of which are the segments that make up this projection.
The following illustration shows how to calculate the length of a subset, the beginning of which is the segment with coordinate 5 :

those. the subset starting at coordinate 5 has a maximum length - len = 4, for a subset starting at coordinate 3, the length will be 2, and so on.
Similarly, running through each segment in the intersection map, we find that the maximally long subset is a subset of length 4 with coordinates in the S1 and S2 lines: 0 and 5, respectively.
As you can see, every step in solving this problem (steps 1, 2, 3) is easily parallelized, Map-Reduce can be used.
1, 2) Each thread is assigned its own segment (or several segments) for which it builds a projection of the segment. In the aggregate, after the corresponding projections are obtained for all the segments, we get a ready intersection map.

3.1) Each thread is assigned its own sequence number (n). Further, the n-th stream, starting from the n-th position, processes each K- th element of the intersection map. Thus, we break the intersection map into several (number of flows) parts. From these parts, choose, in the manner described above, the maximum subsets:
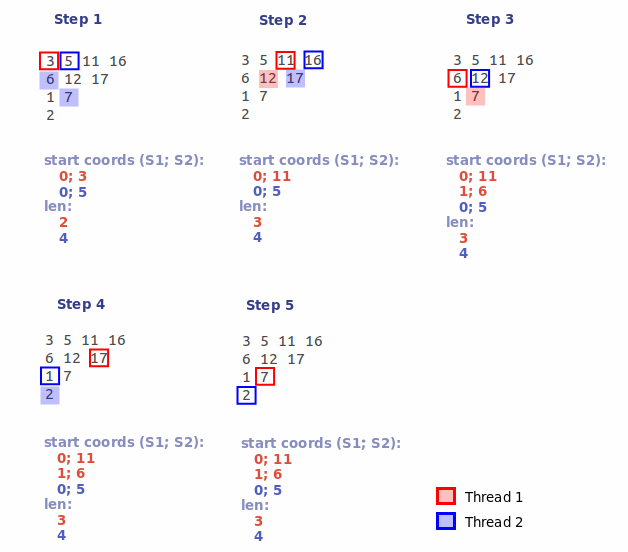
3.2) After all the threads have completed, we will get several groups of subsets. From the received groups we select groups with the maximum length of segments. In our example, these are two groups: a group formed by stream # 1 , containing segments of length 3 characters (with initial coordinates: 0; 11 and 1; 6 ), and a group formed by stream # 2 , containing one segment of length 4 characters (with coordinates 0; 5). Since the second group has the longest segment length, we immediately discard the first group.
As a result, we obtained the initial coordinates of the subset ( 0; 5 ) and its length - 4 . To find the final coordinates, we apply the formula: end_coord = start_coord + len - 1.
Thus we get the answer: 0 3 5 8 .
I decided not to touch upon the details of the implementation of this algorithm in C ++, since this is already beyond the scope of this article. You can get acquainted with the implementation of this algorithm in C ++ (C ++ 11) here , for compiling with GCC, we do not forget to set the -pthread and -std = ++ 0X flags.
This algorithm came to my mind as an obvious solution to the problem, but I do not know if it has a formal name and / or a formal description?
- Share with all the interesting algorithm and its implementation in C ++ (standard C ++ 11);
- Find out if this algorithm has a name and / or a formal description;
Prehistory
It all started with a competition held by Intel, which I learned from the post . The essence of the competition came down to the development and implementation of an algorithm that solves the problem of finding the common substring in two strings as long as possible (I think it makes no sense to rewrite the whole task here). The reference code was attached to the problem, i.e. decision on which it was necessary to "be equal". A little later, from the forum dedicated to this competition, it became clear that the reference code does not solve this problem in the form in which it is formulated on the Intel website. Those. the whole point of the competition was as follows: “to make a program that exactly repeats the output of the reference code, with the same input parameters, only so that it is faster and more parallel”.
Well, okay, even despite the absurdity of the situation with the description of the task, I immediately rejected participation in the competition also because only students and graduates could participate there. I liked the task itself, the one that is described on the site.
Formulation of the problem
Here is how I understood from the description this task:
There are two strings S1 and S2 , you need to find the longest common substring (s) (hereafter, we will call the desired substrings - subsets), the length of which is not less than M. As a result, output its coordinates.
The coordinates are four integers.
The first two refer to the string S1 - the position numbers of the first and last characters of the found substring.
The second two numbers have the same meaning, only refer to the second line - S2 .
For example, if we have the following input parameters:
')
S1 = ABCCA
S2 = ACCABABCCBAABCBAABCBACBACBACBAC
M = 2
then the answer will be:
0 3 5 8
(in the original formulation of the problem, the coordinates need to be output starting from 1, but these are details of the result output, and they do not belong to the algorithm itself).
Also in the requirements for the task there is one more additional input parameter K - the number of threads that can be used to parallelize the algorithm.
Let us sum up what is given to us at the entrance:
- S1 , S2 - two lines in which you want to search;
- M is the minimum possible length of the required substring;
- K is the number of threads that can be used for parallelization;
Algorithm
In fact, the idea of the solution is very simple and consists of 3 steps:
- Split S1 into the smallest possible (length M ) segments.
- Project segments on S2 .
- On the resulting projection, find the longest subsets (consisting of the maximum number of consecutive segments).
Consider the operation of the algorithm in the following example:
S1 = ABCCA
S2 = ACCABABCCBAABCBAABCBACBACBACBAC
M = 2
K = 2
1) Split S1 into segments, each with a length of M = 2:
AB , BC , CC , CA
2) We project each resulting segment on S2 :

or in the form of offsets:

so we got the projection of S1 to S2 :

we will call this projection - the intersection map.
In fact, the intersection map is a matrix of coordinates of all segments whose length is equal to M. Those. each element of the matrix characterizes the coordinate in row S2 , while the row number of the matrix characterizes the coordinate in row S1 . Having the intersection map at our disposal, we can find all the intersections (subsets) and choose the maximum ones.
3) Search for maximum subsets (a set of segments).
If you look at the intersection map in symbolic form, you can already visually find the longest subset:

If we take into account that each segment can serve as the beginning of a subset, then using the intersection map, we can calculate the length of all subsets, the beginning of which are the segments that make up this projection.
The following illustration shows how to calculate the length of a subset, the beginning of which is the segment with coordinate 5 :

those. the subset starting at coordinate 5 has a maximum length - len = 4, for a subset starting at coordinate 3, the length will be 2, and so on.
Similarly, running through each segment in the intersection map, we find that the maximally long subset is a subset of length 4 with coordinates in the S1 and S2 lines: 0 and 5, respectively.
Paralleling
As you can see, every step in solving this problem (steps 1, 2, 3) is easily parallelized, Map-Reduce can be used.
1, 2) Each thread is assigned its own segment (or several segments) for which it builds a projection of the segment. In the aggregate, after the corresponding projections are obtained for all the segments, we get a ready intersection map.

3.1) Each thread is assigned its own sequence number (n). Further, the n-th stream, starting from the n-th position, processes each K- th element of the intersection map. Thus, we break the intersection map into several (number of flows) parts. From these parts, choose, in the manner described above, the maximum subsets:

3.2) After all the threads have completed, we will get several groups of subsets. From the received groups we select groups with the maximum length of segments. In our example, these are two groups: a group formed by stream # 1 , containing segments of length 3 characters (with initial coordinates: 0; 11 and 1; 6 ), and a group formed by stream # 2 , containing one segment of length 4 characters (with coordinates 0; 5). Since the second group has the longest segment length, we immediately discard the first group.
As a result, we obtained the initial coordinates of the subset ( 0; 5 ) and its length - 4 . To find the final coordinates, we apply the formula: end_coord = start_coord + len - 1.
Thus we get the answer: 0 3 5 8 .
Conclusion
I decided not to touch upon the details of the implementation of this algorithm in C ++, since this is already beyond the scope of this article. You can get acquainted with the implementation of this algorithm in C ++ (C ++ 11) here , for compiling with GCC, we do not forget to set the -pthread and -std = ++ 0X flags.
Question
This algorithm came to my mind as an obvious solution to the problem, but I do not know if it has a formal name and / or a formal description?
Source: https://habr.com/ru/post/145198/
All Articles