Work with isometric matrices. Part 1
Isometry is a thing as old as computer games.
Now is the time when the Internet and games began to be combined in the browser (flash does not count).
There are many examples of browser games, most of them are casual games, but for geeks action, RTS and RPG genres are more interesting, and for developers, their implementation.
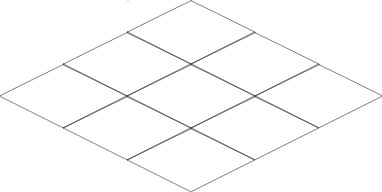
For the genre of RTS, RPG and step-by-step strategies, the matrix is the main mechanism for moving units, drawing textures and more. But when you try to combine the matrix and isometric textures, you will go to hell, from which you will not come out until you write a layer for controlling and influencing this matrix.
')
Under the cut, I will tell:
It is quite simple to draw an ordinary square matrix, it is symmetric, the search for coordinates is generally not a difficult task, but isometric matrices introduce 2 corrections to the work:
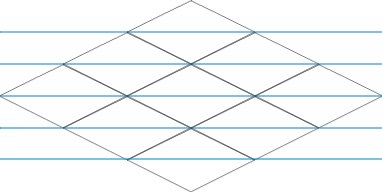
All these problems must be taken into account during implementation.
As mentioned in the first paragraph of the features of the isometric matrix, the drawing should come from the center of the canvas. So we need the middle of the canvas.
In the second paragraph you should pay attention to the visual deception. The brain, looking at the image, wants to draw it horizontally, but it needs to be done diagonally, as shown in the next image.
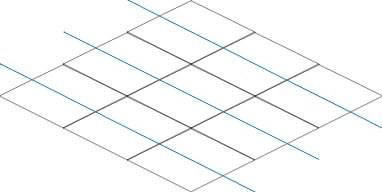
We have already examined the most basic problems, let's look at the implementation.
Everything is commented out, there is a working example, so you can see everything yourself.
Here is a finished example.
Well, we were able to draw an isometric matrix, now we need to draw it in fullscreen.
With her a little more complicated, but rather:
In practice, when drawing the standard matrix, we get an empty area in the form of a triangle,
which means we can calculate the unknown side and make a shift along its height so that there are no holes left.
We know the length of one leg and we can easily find out the length of the hypotinuse.
Side A is the known length of the leg (the width of the entire drawing area divided by 2). Those. 1024px / 2 = 512px, leg length A
side B - we do not know this leg, it will need to be calculated.
side C - Hypotenuse, to find out its length, we need to calculate the length of one of the sides of our small diamond.
To do this, take half of the width and half of the height of the rhombus, put them in a square and sum it up, and calculate the square root of the result.
Once we have calculated the length of one face of a rhombus, we must take half the width of the canvas, divide it by 32 and multiply the result by the length of the face of the rhombus.
Next, we give the well-known leg and the hypotenuse squared. We take away the leg from the hypotenuse, and calculate the square root of the result.
Everything, the equation is solved, it now remains to apply the result in the calculations of the drawing.
As you can see from this example , now we draw a rhombus so that there is no hole on top.
But now there was a problem number 2. It is necessary to calculate the additional height and width of the area.
This is not difficult to do, but now we abandon the static width or height of the matrix.
If the width is greater than the height, then the width must be divided by 32, otherwise the height
Well, as I said, we have a third problem. We are trying to draw areas that are outside the canvas.
This can be limited to the usual condition for the width and height of the canvas, but with an additional increase in the width and height of the image,
so that there are no empty areas.
That's all. Here is a complete example . Now you have learned how to draw full-fledged isometric matrices, but this is only half the battle.
It will be harder to find entries in the matrix, i.e. calculate which coordinate of the matrix was clicked and, in the case of calling the coordinate, calculate exactly where the center of this coordinate is. But more about that in the next article.
Now is the time when the Internet and games began to be combined in the browser (flash does not count).
There are many examples of browser games, most of them are casual games, but for geeks action, RTS and RPG genres are more interesting, and for developers, their implementation.

For the genre of RTS, RPG and step-by-step strategies, the matrix is the main mechanism for moving units, drawing textures and more. But when you try to combine the matrix and isometric textures, you will go to hell, from which you will not come out until you write a layer for controlling and influencing this matrix.
')
Under the cut, I will tell:
- How to draw an isometric matrix
- How to draw a fullscreen isometric matrix
Introduction
It is quite simple to draw an ordinary square matrix, it is symmetric, the search for coordinates is generally not a difficult task, but isometric matrices introduce 2 corrections to the work:
- Drawing the matrix should occur from the center of the canvas.
- Visual deception of rendering.

All these problems must be taken into account during implementation.
Matrix rendering
As mentioned in the first paragraph of the features of the isometric matrix, the drawing should come from the center of the canvas. So we need the middle of the canvas.
In the second paragraph you should pay attention to the visual deception. The brain, looking at the image, wants to draw it horizontally, but it needs to be done diagonally, as shown in the next image.

We have already examined the most basic problems, let's look at the implementation.
Everything is commented out, there is a working example, so you can see everything yourself.
Drawing implementation
var element = document.getElementById('canvas'); element.width = 1024; element.height = 512; var ctx = element.getContext('2d'); var image = new Image(); image.src = 'http://habrastorage.org/storage2/e61/42d/5b2/e6142d5b26d171611d60d5941e390398.png'; // var width = 128; var height = 64; image.onload = function() { function draw(x, y) { ctx.drawImage(image, x - width / 2, y - height / 2, width, height); } // X Y . // , // , . var Xo = 0; var Yo = 0; // var C = Math.floor(element.width / 2); // X, // Y var Xc = 0; var matrixHeight = 8; var matrixWidth = 8; for(var y = 0; y < matrixHeight; y++) { // , Yo = (height / 2) * y; // . Xc = C - (width / 2 * y); for(var x = 0; x < matrixWidth; x++) { // X . // , . // Xo = Xc + (x * (width / 2)); // Y. // X, // X, Y. Yo += height / 2; draw(Xo, Yo); } } } Here is a finished example.
Drawing fullscreen matrix
Well, we were able to draw an isometric matrix, now we need to draw it in fullscreen.
With her a little more complicated, but rather:
- Calculate the total height of the shift matrix
- It is necessary to calculate the additional height and width of the matrix, with which the empty area will be filled.
- Put restrictions on rendering invisible areas
Theory and practice of calculating the total shear height of the matrix
In practice, when drawing the standard matrix, we get an empty area in the form of a triangle,
which means we can calculate the unknown side and make a shift along its height so that there are no holes left.
We know the length of one leg and we can easily find out the length of the hypotinuse.
Side A is the known length of the leg (the width of the entire drawing area divided by 2). Those. 1024px / 2 = 512px, leg length A
side B - we do not know this leg, it will need to be calculated.
side C - Hypotenuse, to find out its length, we need to calculate the length of one of the sides of our small diamond.
To do this, take half of the width and half of the height of the rhombus, put them in a square and sum it up, and calculate the square root of the result.
... var width = 128; var height = 64; var grainLength = Math.sqrt((width / 2) * (width / 2) + (height / 2) * (height / 2)); // 71.554 // , 64px 128px image.onload = function() { ... Once we have calculated the length of one face of a rhombus, we must take half the width of the canvas, divide it by 32 and multiply the result by the length of the face of the rhombus.
... var grainLength = Math.sqrt((width / 2) * (width / 2) + (height / 2) * (height / 2)); var center = Math.floor(element.width / 2); var hypotenuse = center / (width / 2) * grainLength; image.onload = function() { ... Next, we give the well-known leg and the hypotenuse squared. We take away the leg from the hypotenuse, and calculate the square root of the result.
... var hypotenuse = center / (width / 2) * grainLength; var catheusA = center * center; hypotenuse *= hypotenuse; // , . var catheusB = Math.sqrt(hypotenyse - catheusA); image.onload = function() { ... Everything, the equation is solved, it now remains to apply the result in the calculations of the drawing.
... for(var y = 0; y < matrixHeight; y++) { Yo = (height / 2) * y; Xc = C - (64 * y); ... As you can see from this example , now we draw a rhombus so that there is no hole on top.
But now there was a problem number 2. It is necessary to calculate the additional height and width of the area.
This is not difficult to do, but now we abandon the static width or height of the matrix.
If the width is greater than the height, then the width must be divided by 32, otherwise the height
... var matrixHeight = (element.width > element.height ? element.width : element.height) / 32; var matrixWidth = (element.width > element.height ? element.width : element.height) / 32; ... Well, as I said, we have a third problem. We are trying to draw areas that are outside the canvas.
This can be limited to the usual condition for the width and height of the canvas, but with an additional increase in the width and height of the image,
so that there are no empty areas.
... Xo = Xc + (x * 64); Yo += 32; if(Xo < (width / -1) || Xo > element.width + width || Yo < (height / -1) || Yo > element.height + height) continue; draw(Xo, Yo); ... That's all. Here is a complete example . Now you have learned how to draw full-fledged isometric matrices, but this is only half the battle.
It will be harder to find entries in the matrix, i.e. calculate which coordinate of the matrix was clicked and, in the case of calling the coordinate, calculate exactly where the center of this coordinate is. But more about that in the next article.
Source: https://habr.com/ru/post/145141/
All Articles