Introduction to modular arithmetic
In ordinary life, we usually use the positional number system. In the positional number system, the value of each numeric character (number) in the number record depends on its position (digit) [1]. However, there are also so-called “nonpositional numeral systems”, one of which is the “residual class system” (SOC) (or the original Residue Number System (RNS)), which is the basis of modular arithmetic. Modular arithmetic is based on the “Chinese remainder theorem” [2], which for our case is as follows:
At first glance, it is unclear what advantage such a system can give, however, there are 2 properties that allow you to effectively use modular arithmetic in some areas of microelectronics:
But not everything is as smooth as we would like. Unlike the positional number system, the following operations (called “non-modular”) are more complicated than in the positional number system: comparison of numbers, control of overflow, division, square root, etc. The first successful attempts to use modular arithmetic in microelectronics were made as early as the 1950s, but due to difficulties with non-modular operations, interest has somewhat subsided. However, at present, modular arithmetic is again being returned to microelectronics for the following reasons:
At present, modular arithmetic is used in the following areas: digital signal processing, cryptography, image / audio / video processing, etc.
Direct conversion from a positional number system (usually in binary form) to a number system in the residuals consists in finding the residuals from the division for each of the modules of the system.
')
The implementation of finding a deduction in microelectronics for a given module is based on the following properties of deductions:
(a + b)% p = (a% p + b% p)% p
(a * b)% p = (a% p * b% p)% p
Any number X can be written as X% p = (x n-1 * 2 n-1 + x n-2 * 2 n-2 + x 0 * 2 0 )% p = ((x n-1 )% p * 2 n-1 % p) + ((x n-2 )% p * 2 n-2 % p) + ... + x 0 % p)% p. Since in this case x n-1 , ... x 0 is equal to 0 or 1, we actually need to add residues of the form (2 i % p).
The system of modules used is selected for a specific task. For example, to represent 32-bit numbers, the following system of modules is enough: (7, 11, 13, 17, 19, 23, 29, 31) - they are all mutually simple with each other, their product is 6685349671> 4294967296. Each of the modules is not exceeds 5 bits, that is, addition and multiplication operations will be performed on 5-bit numbers.
Of particular importance is also the system of modules of the form: (2 n -1, 2 n , 2 n +1) due to the fact that the direct and inverse transformations for them are carried out in the simplest way. To get the remainder of the division by 2 n, it suffices to take the last n digits of the binary representation of a number.
The inverse conversion from the number system in the residual classes to the positional number system is performed in one of two ways:
The rest of the methods proposed in various literature are essentially a mixture of these two.
The method based on the Chinese theorem on residuals is based on the following idea:
X = (x 1 , x 2 , ... x n ) = (x 1 , 0, ..., 0) + (0, x 2 , ..., 0) + ... + (0, 0, ..., x n ) = x 1 * (1, 0, ..., 0) + x 2 * (0, 1, ..., 0) + ... + x n * (0, 0, ..., 1).
That is, for the inverse transformation, it is required to find the system of orthogonal bases B1 = (1, 0, ..., 0), B2 = (0, 1, ..., 0), ..., BN = (0, 0, ..., 1). These vectors are found once for a given basis, and for their search it is required to solve an equation of the form: (M i * b i )% p i = 1, where M i = M / p i , and b i is the required number. In this case, the positional representation of B i = M i * b i and
X = (x 1 * (M 1 * b 1 ) + x 2 * (M 2 * b 2 ) +… + x n * (M n * b n ))% M
The disadvantage of this method is that the inverse transformation requires multiplication and addition of large numbers (M 1 , ..., M n ), as well as the operation of taking the remainder modulo a large number M.
The method based on the polyadic code is based on the idea that any number X can be represented in the system of coprime numbers p 1 , ... p n , as [4]:
X = a 1 + a 2 * p 1 + a 3 * p 1 * p 2 + ... + a n-1 * p 1 * p 2 * ... * p n-2 + a n * p 1 * p 2 * ... * p n-1 , where 0 <a i <p i
To use this method, constants of the form (p i -1 )% p k -1 are required. You may also notice that you can start calculating a 3 as soon as the value a 1 appears. Based on this method, you can build a conveyor converters.
The article is written somewhat messy, because the topic is quite large and it is not possible to contain everything in one article. In the following articles I will try to describe in more detail the various aspects of modular arithmetic. On Habré, I did not find anything at all related to this topic, only brief mentions in other articles, so it was decided to write a short review with simple examples. For those who are interested in the topic, I recommend reading the book number [3] from the list of references (in English), it is written in an accessible language with many examples.
[1] en.wikipedia.org/wiki/%D0%9F%D0%BE%D0% B7% D0% B8% D1% 86% D0% B8% D0% BE% D0% BD% D0% BD% D0% B0% D1% 8F_% D1% 81% D0% B8% D1% 81% D1% 82% D0% B5% D0% BC% D0% B0_% D1% 81% D1% 87% D0% B8% D1% 81% D0% BB% D0% B5% D0% BD% D0% B8% D1% 8F
[2] en.wikipedia.org/wiki/%D0%9A%D0%B8%D1%82%D0%B0%D0%B9%D1%81 %D0BA0DB %%D0 82% D0% B5% D0% BE% D1% 80% D0% B5% D0% BC% D0% B0_% D0% BE% D0% B1_% D0% BE% D1% 81% D1% 82% D0% B0% D1% 82% D0% BA% D0% B0% D1% 85
[3] Amos Omondi, Benjamin Premkumar, Residue Number Systems: Theory and Implementation, 2007.
[4] MA Soderstrand, WK Jenkins, GA Jullien and FJ Taylor. 1986. Residue Number System Arithmetic: Modern Applications in Digital Signal Processing, IEEE Press, New York.
For any system of mutually prime numbers p 1 , ... p n , any number X from the range [0; M), where M = p 1 * p 2 * ... * p p n is mutually uniquely representable as a vector (a 1 , a 2 , ..., a n ), where a i = X% p i (hereinafter "%" - the operation of taking the remainder of the integer division of X by p i ).
p 1 , ... p n - system modules
a 1 , a 2 , ..., a n - residues (deductions) of numbers according to a given system of modules
At first glance, it is unclear what advantage such a system can give, however, there are 2 properties that allow you to effectively use modular arithmetic in some areas of microelectronics:
- Lack of transfer of discharges in addition and multiplication. Let us be given two numbers X 1 and X 2 , represented as a system of residuals (x 11 , x 12 , ..., x 1n ) and (x 21 , x 22 , ..., x 2n ) in the system of mutually simple numbers (p 1 , p 2 , ..., p n ). In this case:
X 3 = X 1 + X 2 = ((x 11 + x 21 )% p 1 , (x 12 + x 22 )% p 2 , ..., (x 1n + x 2n )% p n )
X 4 = X 1 * X 2 = ((x 11 * x 21 )% p 1 , (x 12 * x 22 )% p 2 , ..., (x 1n * x 2n )% p n )
That is, to add or multiply two numbers, it is enough to add or multiply the corresponding elements of the vector, which for microelectronics means that this can be done in parallel and due to the small dimensions p 1 , p 2 , ..., p n to do it very quickly. - Error in one position of the vector does not affect the calculations in other positions of the vector. In contrast to the positional number system, all elements of the vector are equivalent and an error in one of them only leads to a reduction in the dynamic range. This fact allows you to design devices with high fault tolerance and error correction.
| Normal multiplication | Modular multiplication |
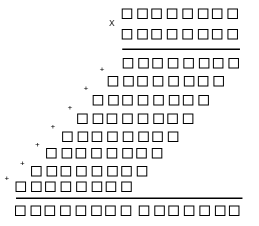 |  |
But not everything is as smooth as we would like. Unlike the positional number system, the following operations (called “non-modular”) are more complicated than in the positional number system: comparison of numbers, control of overflow, division, square root, etc. The first successful attempts to use modular arithmetic in microelectronics were made as early as the 1950s, but due to difficulties with non-modular operations, interest has somewhat subsided. However, at present, modular arithmetic is again being returned to microelectronics for the following reasons:
- large distribution of mobile processors, which require high speed with low power consumption. The absence of transference in arithmetic operations of addition / multiplication reduces energy consumption.
- The increasing density of elements on a chip in some cases does not allow for a full test, therefore the importance of the stability of processors to possible errors grows.
- the emergence of specialized processors with a large number of operations on vectors that require high speed and mainly include addition and multiplication of numbers (as an example, matrix multiplication, scalar product of vectors, Fourier transforms, etc.).
At present, modular arithmetic is used in the following areas: digital signal processing, cryptography, image / audio / video processing, etc.
Direct conversion
Direct conversion from a positional number system (usually in binary form) to a number system in the residuals consists in finding the residuals from the division for each of the modules of the system.
')
Example : Suppose you want to find a representation of the number X = 25 by the system of modules (3, 5, 7). X = (25% 3, 25% 5, 25% 7) = (1, 0, 4).
The implementation of finding a deduction in microelectronics for a given module is based on the following properties of deductions:
(a + b)% p = (a% p + b% p)% p
(a * b)% p = (a% p * b% p)% p
Any number X can be written as X% p = (x n-1 * 2 n-1 + x n-2 * 2 n-2 + x 0 * 2 0 )% p = ((x n-1 )% p * 2 n-1 % p) + ((x n-2 )% p * 2 n-2 % p) + ... + x 0 % p)% p. Since in this case x n-1 , ... x 0 is equal to 0 or 1, we actually need to add residues of the form (2 i % p).
Example : let the number 25 be given or in binary notation 11001 and it is required to find the remainder modulo 7.
25% 7 = (1 * 2 4 + 1 * 2 3 + 0 * 2 2 + 0 * 1 + 1 * 2 0 )% 7 = (2 4 % 7 + 2 3 % 7 + 1% 7)% 7 = (2 + 1 + 1)% 7 = 4
The system of modules used is selected for a specific task. For example, to represent 32-bit numbers, the following system of modules is enough: (7, 11, 13, 17, 19, 23, 29, 31) - they are all mutually simple with each other, their product is 6685349671> 4294967296. Each of the modules is not exceeds 5 bits, that is, addition and multiplication operations will be performed on 5-bit numbers.
Of particular importance is also the system of modules of the form: (2 n -1, 2 n , 2 n +1) due to the fact that the direct and inverse transformations for them are carried out in the simplest way. To get the remainder of the division by 2 n, it suffices to take the last n digits of the binary representation of a number.
Arithmetic operations
Example : let the system of modules (3, 5, 7) be given, that is, we can perform operations whose result does not exceed 3 * 5 * 7 = 105. Multiply two numbers 8 and 10.
8 = (8% 3, 8% 5, 8% 7) = (2, 3, 1)
10 = (10% 3, 10% 5, 10% 7) = (1, 0, 3)
8 * 10 = ((2 * 1)% 3, (3 * 0)% 5, (1 * 3)% 7) = (2, 0, 3)
Check
80 = (80% 3, 80% 5, 80% 7) = (2, 0, 3)
Inverse transform
The inverse conversion from the number system in the residual classes to the positional number system is performed in one of two ways:
- Based on the Chinese theorem on residues or a system of orthogonal bases
- Based on polyadic code (other names are mixed-radix system, mixed base system)
The rest of the methods proposed in various literature are essentially a mixture of these two.
The method based on the Chinese theorem on residuals is based on the following idea:
X = (x 1 , x 2 , ... x n ) = (x 1 , 0, ..., 0) + (0, x 2 , ..., 0) + ... + (0, 0, ..., x n ) = x 1 * (1, 0, ..., 0) + x 2 * (0, 1, ..., 0) + ... + x n * (0, 0, ..., 1).
That is, for the inverse transformation, it is required to find the system of orthogonal bases B1 = (1, 0, ..., 0), B2 = (0, 1, ..., 0), ..., BN = (0, 0, ..., 1). These vectors are found once for a given basis, and for their search it is required to solve an equation of the form: (M i * b i )% p i = 1, where M i = M / p i , and b i is the required number. In this case, the positional representation of B i = M i * b i and
X = (x 1 * (M 1 * b 1 ) + x 2 * (M 2 * b 2 ) +… + x n * (M n * b n ))% M
Example : Let the system of modules (3, 5, 7) be given, find the values of M i and b i (0 <i <= 3)
M = 3 * 5 * 7 = 105
M 1 = 105/3 = 35
M 2 = 105/5 = 21
M 3 = 105/7 = 15
(35 * b 1 )% 3 = 1 => b 1 = 2
(21 * b 2 )% 5 = 1 => b 2 = 1
(15 * b 3 )% 7 = 1 => b 3 = 1
Now we transform any number in the system of residual classes. Set
X = (2, 3, 1) = (2 * 35 * 2 + 3 * 21 * 1 + 1 * 15 * 1)% 105 = (140 + 63 + 15)% 105 = 218% 105 = 8
The disadvantage of this method is that the inverse transformation requires multiplication and addition of large numbers (M 1 , ..., M n ), as well as the operation of taking the remainder modulo a large number M.
The method based on the polyadic code is based on the idea that any number X can be represented in the system of coprime numbers p 1 , ... p n , as [4]:
X = a 1 + a 2 * p 1 + a 3 * p 1 * p 2 + ... + a n-1 * p 1 * p 2 * ... * p n-2 + a n * p 1 * p 2 * ... * p n-1 , where 0 <a i <p i
- X% p 1 = x 1 = a 1
- (X - a 1 )% p 2 = (x 2 - a 1 )% p 2 = (a 2 * p 1 )% p 2 => a 2 = ((p 1 -1 )% p 2 * (x 2 - a 1 ))% p 2
- (X - a 1 - a 2 * p 1 )% p 3 = (a 3 * p 1 * p 2 )% p 3 => a 3 = ((p 2 -1 )% p 3 * ((p 1 - 1 )% p 3 * (x 3 - a 1 ) - a 2 ))% p 3
- ...
To use this method, constants of the form (p i -1 )% p k -1 are required. You may also notice that you can start calculating a 3 as soon as the value a 1 appears. Based on this method, you can build a conveyor converters.
Example : Consider the same example - find the positional representation of the number X = (2, 3, 1) in the system of modules (3, 5, 7)
- a 1 = x 1 = 2
- a 2 = ((p 1 -1 )% p 2 * (x 2 - a 1 ))% p 2 = ((3 -1 )% 5 * (3 - 2))% 5 = 2 * 1 = 2
- a 3 = ((p 2 -1 )% p 3 * ((p 1 -1 )% p 3 * (x 3 - a 1 ) - a 2 ))% p 3 = ((5 -1 )% 7 * ((3 -1 )% 7 * (1 - 2) - 2))% 7 = (3 * (5 * (1-2) -2))% 7 = (3 * (- 7))% 7 = 0
- X = a 1 + a 2 * p 1 + a 3 * p 1 * p 2 = a 1 + 3 * a 2 + 15 * a 3 = 2 + 3 * 2 + 15 * 0 = 8
Note : to find a constant of the form (3 -1 )% 5, it is required to solve the equation (3 * x)% 5 = 1, where 0 <= x <5
PS
The article is written somewhat messy, because the topic is quite large and it is not possible to contain everything in one article. In the following articles I will try to describe in more detail the various aspects of modular arithmetic. On Habré, I did not find anything at all related to this topic, only brief mentions in other articles, so it was decided to write a short review with simple examples. For those who are interested in the topic, I recommend reading the book number [3] from the list of references (in English), it is written in an accessible language with many examples.
Literature
[1] en.wikipedia.org/wiki/%D0%9F%D0%BE%D0% B7% D0% B8% D1% 86% D0% B8% D0% BE% D0% BD% D0% BD% D0% B0% D1% 8F_% D1% 81% D0% B8% D1% 81% D1% 82% D0% B5% D0% BC% D0% B0_% D1% 81% D1% 87% D0% B8% D1% 81% D0% BB% D0% B5% D0% BD% D0% B8% D1% 8F
[2] en.wikipedia.org/wiki/%D0%9A%D0%B8%D1%82%D0%B0%D0%B9%D1%81 %D0BA0DB %%D0 82% D0% B5% D0% BE% D1% 80% D0% B5% D0% BC% D0% B0_% D0% BE% D0% B1_% D0% BE% D1% 81% D1% 82% D0% B0% D1% 82% D0% BA% D0% B0% D1% 85
[3] Amos Omondi, Benjamin Premkumar, Residue Number Systems: Theory and Implementation, 2007.
[4] MA Soderstrand, WK Jenkins, GA Jullien and FJ Taylor. 1986. Residue Number System Arithmetic: Modern Applications in Digital Signal Processing, IEEE Press, New York.
Source: https://habr.com/ru/post/144886/
All Articles