Ropes - quick lines
Hello, Habr.
Most of us work with strings anyway. This can not be avoided - if you write a code, you are doomed to add lines every day, break them into components and access individual characters by index. We have long been accustomed to strings being arrays of characters of fixed length, and this entails corresponding restrictions in working with them.
So, we cannot quickly merge two strings - for this we need to first allocate the required amount of memory, and then copy the data there from the concatenated strings. Obviously, such an operation has complexity of the order O (n), where n is the total length of the rows.
That is why the code
works so slowly.
Do you want to concatenate giant strings quickly? Do not like what the line requires to store a continuous area of memory? Tired of using buffers to build strings?
')
The data structure that will save us is called the Rope string , or “rope string”. The principle of its operation is very simple and one can guess it literally from intuitive considerations.
Suppose we need to add two lines:
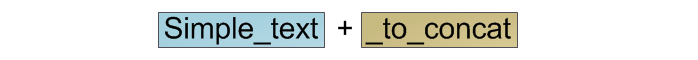
For classic strings, we simply allocate a memory area of the required size, copy the contents of the first row to the beginning, and the second one to the end:
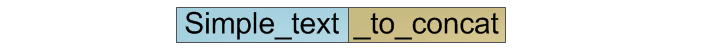
As mentioned above, the complexity of this operation is O (n).
But what if we use the information that our result string is the concatenation of the two source lines? And indeed, create an object that provides a string interface and stores information about its components — source lines:

This way of stitching works in O (1) —we just need to create a wrapper object for the source strings. Since this object is also a string, it can be combined with other strings to get the concatenations we need:
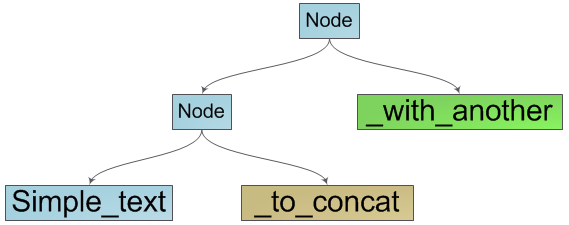
It is already obvious that our structure is a binary search tree, in the leaves of which there are elementary components of our string - groups of characters. It also becomes obvious how to enumerate characters in a string — this is a tree-to-depth traversal with sequential enumeration of characters in the leaves of a tree.
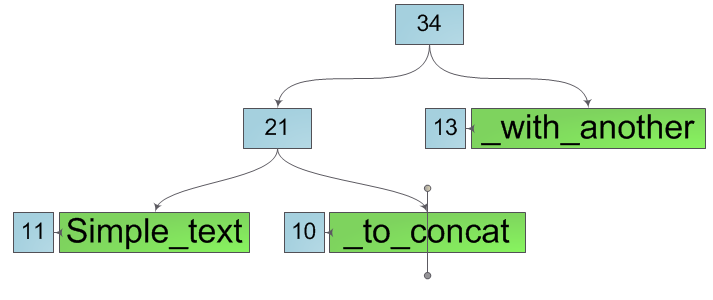
We now implement the operation of obtaining a character string by its index. To do this, we introduce to the nodes of the tree an additional characteristic - weight. If a part of symbols is stored directly in a tree node (node is a leaf), then its weight is equal to the number of these symbols. Otherwise, the weight of the node is equal to the sum of the weights of its descendants. In other words, the weight of a node is the length of the string it represents.
We need to get the i-th character of the string represented by the Node node. Then two cases may arise:
Now we can concatenate strings in O (1) and index the characters in them in O (h) - tree heights. But for complete happiness, you need to learn how to quickly perform splitting operations on two lines, deleting and inserting a substring.
So, we have a string and it is extremely necessary for us to split it into two substrings in some of its position k (the numbers in the diagram are the sizes of the corresponding trees):
The place of "breaking" the line is always in one of the leaves of the tree. We divide this sheet into two new ones that contain substrings of the original sheet. Moreover, for this operation, we will not need to copy the contents of the sheet into new ones, simply enter such sheet characteristics as offset and length and save pointers to the original array of characters in the new sheets, changing only the offset and length:
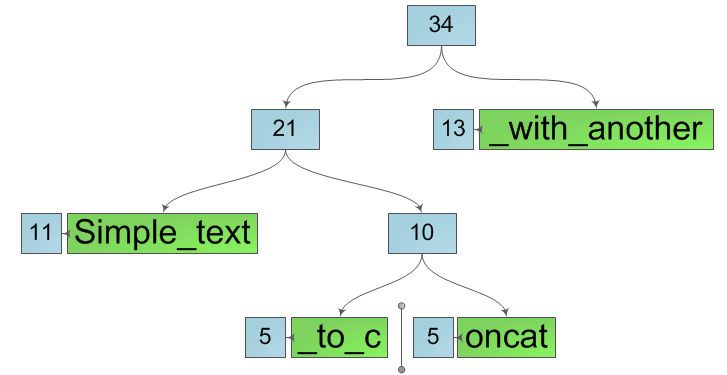
Next, we will split all the nodes on the path from the sheet to the root, creating instead of them pairs of nodes belonging to the left and right substring, respectively. Moreover, we again do not change the current node, but only create two new ones instead. This means the operation of dividing a string generates new substrings without affecting the original one. After splitting the source line, we get two new lines, as in the figure below.

It is easy to see that the internal structure of such lines is not optimal - some are clearly superfluous. However, it is easy to correct this annoying omission - it is enough to walk from the place of the incision to the root in both substrings, replacing each node that has exactly one descendant by this very descendant. After that, all unnecessary nodes will disappear and we will get the required substrings in their final form:

The complexity of the operation of splitting rows is, obviously, O (h).
Thanks to the splitting and merging operations already implemented, deleting and inserting is done elementary - to delete a substring, it is enough to split the source line at the start and end of the deleted section and glue the outermost lines. To insert into strings at a certain position, we divide the source string into two substrings in it and glue them together with the inserted one in the necessary order. Both operations have the asymptotics O (h).
The attentive reader, having heard the word “tree”, would inevitably recall the other two - “logarithm” and “balancing”. And, as always, in order to achieve the cherished logarithmic asymptotics, we will still have to balance our tree. Indeed, with the current method of merging lines, the internal structure of the tree will look more like a “ladder”, for example, such as in the figure below:
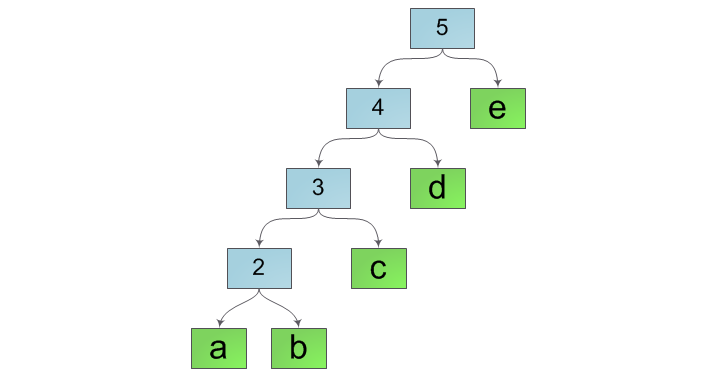
To avoid this, we will check the balance of the result with each join of the rows and, if necessary, reassemble the entire tree, balancing it. A good balance condition is that the length of the string must be at least (h + 2) - th Fibonacci number. The justification of this condition and a couple of additional modifications of the splicing operation were given by Boehm, Atkinson and Plass in their work Ropes: an Alternative to Strings
The storage of tree nodes is not at all free. If we add one character to the line, then we spend to store information about tree nodes an order of magnitude more memory than the characters themselves. In order to avoid such situations, as well as to reduce the height of the tree, it is advisable to glue strings smaller than a certain length (for example, 32) in a “classical” way. This greatly saves memory and also has almost no effect on overall performance.
In the overwhelming number of cases, we iterate over the characters of a string sequentially. In our case, if we request characters by indices i and i + 1, there is a very high probability that they are physically located in the same leaf of the tree. This means that when searching for these characters we will repeat the same path from the root of the tree to the leaf. The obvious solution to this problem is caching. To do this, when searching for the next character, remember the sheet in which it is located and the range of indices that this sheet contains in itself. After, when searching for the next character, we will first check whether our index lies in the memorized range and, if so, we will look for it directly in the memorized list. You can even go further, remembering not one last position but several, for example, in the cyclic list.
Together with the previous optimization, such a technique will allow us to improve the asymptotics of indexation from O (ln (n)) to almost O (1).
What we get as a result? We will get a persistent string implementation that does not require a continuous memory region for its storage, with logarithmic asymptotics for insertion, deletion and concatenation (instead of O (n) on classic strings) and indexing almost O (1) - a result worthy of attention.
And finally, here are a couple of useful links: an article in the English wiki , a Java implementation and a description of the C ++ implementation on the SGI site .
Use the ropes, Luke!
Most of us work with strings anyway. This can not be avoided - if you write a code, you are doomed to add lines every day, break them into components and access individual characters by index. We have long been accustomed to strings being arrays of characters of fixed length, and this entails corresponding restrictions in working with them.
So, we cannot quickly merge two strings - for this we need to first allocate the required amount of memory, and then copy the data there from the concatenated strings. Obviously, such an operation has complexity of the order O (n), where n is the total length of the rows.
That is why the code
string s = ""; for (int i = 0; i < 100000; i++) s += "a"; works so slowly.
Do you want to concatenate giant strings quickly? Do not like what the line requires to store a continuous area of memory? Tired of using buffers to build strings?
')
The data structure that will save us is called the Rope string , or “rope string”. The principle of its operation is very simple and one can guess it literally from intuitive considerations.
Idea
Suppose we need to add two lines:
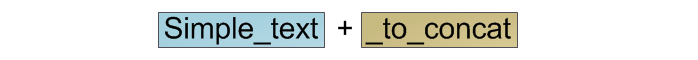
For classic strings, we simply allocate a memory area of the required size, copy the contents of the first row to the beginning, and the second one to the end:
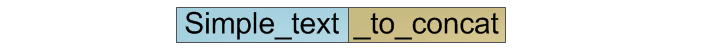
As mentioned above, the complexity of this operation is O (n).
But what if we use the information that our result string is the concatenation of the two source lines? And indeed, create an object that provides a string interface and stores information about its components — source lines:

This way of stitching works in O (1) —we just need to create a wrapper object for the source strings. Since this object is also a string, it can be combined with other strings to get the concatenations we need:

It is already obvious that our structure is a binary search tree, in the leaves of which there are elementary components of our string - groups of characters. It also becomes obvious how to enumerate characters in a string — this is a tree-to-depth traversal with sequential enumeration of characters in the leaves of a tree.
Indexing
We now implement the operation of obtaining a character string by its index. To do this, we introduce to the nodes of the tree an additional characteristic - weight. If a part of symbols is stored directly in a tree node (node is a leaf), then its weight is equal to the number of these symbols. Otherwise, the weight of the node is equal to the sum of the weights of its descendants. In other words, the weight of a node is the length of the string it represents.
We need to get the i-th character of the string represented by the Node node. Then two cases may arise:
- Knot - list. Then it contains the data itself and it is enough for us to return the i-th character of the “inner” line.
- The node is compound. Then you need to know in which descendant of the node should continue the search. If the weight of the left descendant is greater than i, the required character is the i-th character of the left substring, otherwise it is the (iw) -th character of the right substring, where w is the weight of the left subtree.
Now we can concatenate strings in O (1) and index the characters in them in O (h) - tree heights. But for complete happiness, you need to learn how to quickly perform splitting operations on two lines, deleting and inserting a substring.
Splitting
So, we have a string and it is extremely necessary for us to split it into two substrings in some of its position k (the numbers in the diagram are the sizes of the corresponding trees):

The place of "breaking" the line is always in one of the leaves of the tree. We divide this sheet into two new ones that contain substrings of the original sheet. Moreover, for this operation, we will not need to copy the contents of the sheet into new ones, simply enter such sheet characteristics as offset and length and save pointers to the original array of characters in the new sheets, changing only the offset and length:

Next, we will split all the nodes on the path from the sheet to the root, creating instead of them pairs of nodes belonging to the left and right substring, respectively. Moreover, we again do not change the current node, but only create two new ones instead. This means the operation of dividing a string generates new substrings without affecting the original one. After splitting the source line, we get two new lines, as in the figure below.

It is easy to see that the internal structure of such lines is not optimal - some are clearly superfluous. However, it is easy to correct this annoying omission - it is enough to walk from the place of the incision to the root in both substrings, replacing each node that has exactly one descendant by this very descendant. After that, all unnecessary nodes will disappear and we will get the required substrings in their final form:

The complexity of the operation of splitting rows is, obviously, O (h).
Delete and insert
Thanks to the splitting and merging operations already implemented, deleting and inserting is done elementary - to delete a substring, it is enough to split the source line at the start and end of the deleted section and glue the outermost lines. To insert into strings at a certain position, we divide the source string into two substrings in it and glue them together with the inserted one in the necessary order. Both operations have the asymptotics O (h).
Optimization
Balancing
The attentive reader, having heard the word “tree”, would inevitably recall the other two - “logarithm” and “balancing”. And, as always, in order to achieve the cherished logarithmic asymptotics, we will still have to balance our tree. Indeed, with the current method of merging lines, the internal structure of the tree will look more like a “ladder”, for example, such as in the figure below:

To avoid this, we will check the balance of the result with each join of the rows and, if necessary, reassemble the entire tree, balancing it. A good balance condition is that the length of the string must be at least (h + 2) - th Fibonacci number. The justification of this condition and a couple of additional modifications of the splicing operation were given by Boehm, Atkinson and Plass in their work Ropes: an Alternative to Strings
Direct concatenation of small lines
The storage of tree nodes is not at all free. If we add one character to the line, then we spend to store information about tree nodes an order of magnitude more memory than the characters themselves. In order to avoid such situations, as well as to reduce the height of the tree, it is advisable to glue strings smaller than a certain length (for example, 32) in a “classical” way. This greatly saves memory and also has almost no effect on overall performance.
Caching the last position
In the overwhelming number of cases, we iterate over the characters of a string sequentially. In our case, if we request characters by indices i and i + 1, there is a very high probability that they are physically located in the same leaf of the tree. This means that when searching for these characters we will repeat the same path from the root of the tree to the leaf. The obvious solution to this problem is caching. To do this, when searching for the next character, remember the sheet in which it is located and the range of indices that this sheet contains in itself. After, when searching for the next character, we will first check whether our index lies in the memorized range and, if so, we will look for it directly in the memorized list. You can even go further, remembering not one last position but several, for example, in the cyclic list.
Together with the previous optimization, such a technique will allow us to improve the asymptotics of indexation from O (ln (n)) to almost O (1).
Total
What we get as a result? We will get a persistent string implementation that does not require a continuous memory region for its storage, with logarithmic asymptotics for insertion, deletion and concatenation (instead of O (n) on classic strings) and indexing almost O (1) - a result worthy of attention.
And finally, here are a couple of useful links: an article in the English wiki , a Java implementation and a description of the C ++ implementation on the SGI site .
Use the ropes, Luke!
Source: https://habr.com/ru/post/144736/
All Articles