TDS and MLS methods of impulse response estimates

Little preface

Looking ahead a bit, I’ll say that I’ve shoveled a fair share of the Russian-speaking segment of the Internet, I could not find an adequate description of the TDS and MLS methods for measuring the impulse characteristics of a room. Therefore, I decided to fill this gap. If this article does not claim to adequacy, then just let it stay here.

- What is all this all about?

In general, the impulse response is the response of the system to the impact in the form of a delta function (Dirac function). Of course, in reality, the delta function cannot be obtained; therefore, we will understand by it a very short and very large signal in amplitude. In the context of room acoustics, the imitation of the delta function can be called a banal clap, the sound of a burst ball or a shot of a starting pistol.

- Why is it necessary?

• Using the impulse response, it is possible to determine a variety of acoustic parameters of the room (for example, the reverberation time or signal-to-noise ratio) and electro-acoustic systems (for example, the path response using the Fourier transform);
• Having the impulse characteristic of the room, you can very easily imitate the sound of any sound in this room. For example, check how you will be heard in the hall where you will read the report tomorrow.

- How is this possible?

This is possible due to the convolution operation. What it is, where and with what it is eaten is very well described here (it is recommended to read for a better understanding).
')

Mini FAQ is over, get down to business

Delta function

As mentioned above, the easiest way to measure the impulse response of a room is, for example, to shoot from the starting pistol at the point where the announcer / performer should be placed, and simply record the sound that reaches the listener's placement point. However, for this method there are a number of problems:

• experiments with test signals in the form of a pistol shot sound are not very repeatable;
• the range of the characteristics they produce is often quite complex;
• the high peak power they produce can create nonlinearities that can change the test result;
• if we try to replace the pistol with a loudspeaker and lose some impulse with it, we can get a problem when the necessary amplitude power does not reach the room.

For these reasons, the impulse response is often measured indirectly — through a technique that uses an impact, which is not a pulse in itself, but a signal that is rather long in time.

Tds

TDS (Time Delay Spectrometry - Time Delay Spectrometry) is a technique for measuring the impulse responses of electro-acoustic systems (as well as audiences) in rooms with noticeable reverberation. So TDS allows you to get three-dimensional (time-energy-frequency) graphics impulse characteristics. Although the conceptual and mathematical basis of TDS has been known for quite some time, this method itself is usually attributed to the achievements of Dr. Richard Heyzer, who first published it in 1967 in the Journal of the Audio Engineering Society.

Consider the use of TDS to measure the pulse characteristics of electroacoustic systems. Since measurements are taken in a room with reverberation, each wave emitted by a loudspeaker will be reflected from the surfaces of the room. Therefore, it is necessary to take into account only direct waves, i.e. need to filter out other sounds brought by the room.



The response is recorded using a bandpass filter tuned to a given frequency. With a change in the frequency of the radiation, the filter is also reset to the new frequency, and the operation is repeated. Since it is necessary to measure the loudspeaker response for a given frequency range (for example, from 20 Hz to 20 kHz - the human hearing range), using this approach you will need to repeat the experiment for each frequency in the range.

One way around this obstacle is to use a linear frequency modulated signal (chirp) as an input. The chirp signal starts from zero frequency and linearly "turns around" to higher frequencies.

Since the input signal “unfolds”, the filter must also “unfold” at the same speed. However, it is necessary to take into account the time during which the wave front reaches the microphone. This time delay is usually constant, as the microphone and speaker do not move relative to each other. The time delay is related to the frequency offset, since the center frequency of the bandpass filter is always slightly behind the frequency of the signal emitted by the speaker.

We extend this technique to measure the impulse characteristics of rooms with reverberation noise. To do this, you simply need to slow down the chirp signal so that acoustic dispersions from the surfaces of the room leak through the tracking filter. In essence, the goal is to achieve a stationary equilibrium at each frequency in a room before switching to a new frequency.

Since it is assumed that the system under study is linear and invariant in time, it can be assumed that each reflecting surface is an image of a loudspeaker. A room is a collection of images, each of which has its own unique transfer function, which is described by the product of the spectral dissipation energy S (ω) and the phase component e ^-jωt . Impulse response is the sum of all single responses:





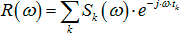
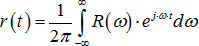
TDS-method requires that the duration of the test signal was much longer than the duration of the response of the system. Thus, if the room being measured has a reverberation time of one second, the duration of the test signal must be at least 10 seconds.

To obtain the impulse response, you can use a chirp signal of any duration, resulting in a larger signal-to-noise ratio in a noisy room. The disadvantage is that the system under test (ie, the room) should be linear and stationary in time (ie, there should be, for example, no air flow).

Mls

MLS (Maximum length sequence - maximum length sequence) is a name in the signal processing of a periodic pseudo-random sequence of values ​​1 and -1. The same name has a cost-effective method for measuring the impulse response of a linear system using the MLS sequence as an input signal. The period of such a signal is:



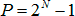
N is the order of the sequence, i.e. the number of changing registers used to generate a sequence.


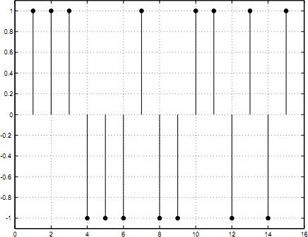
_{MLS sequence (N = 15)}

The result of the autocorrelation function of such a sequence is the delta function. This means that the impulse response of the room is estimated using a cross-correlation function between the original MLS signal and the signal at the receiving point.


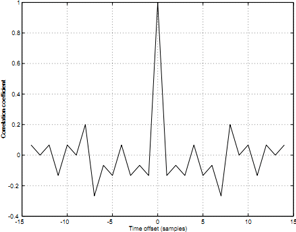
<sub>The autocorrelation function of the MLS sequence (N = 15)


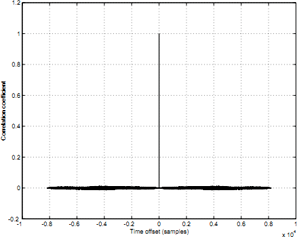
The autocorrelation function of the MLS sequence (N = 8191)</sub>

The cross-correlation function is calculated using the Walsh – Hadamard transform - a special case of the generalized Fourier transform, in which the Walsh function system is the basis. This family of functions that form an orthogonal system takes on values ​​of only 1 and -1 over the entire domain of definition.

A convenient measure of how much energy a signal has per unit of time is the peak factor — the ratio of the amplitude value of the signal to the average:



Ideally, the peak factor should be as close as possible to unity. Since the amplitude and average values ​​are equal, it is impossible to have a larger energy value per unit of time, therefore we can say that the input signal is as close as possible to the ideal pulse.

The MLS sequence peak factor is very close to one, so it makes sense to use this type of signal as an input to achieve a high signal-to-noise ratio during measurements. Because MLS is well suited for setting up an experiment in noisy rooms.

The main requirement of the MLS technique is the linearity of the system under test. The impact must be at least as long as the response. The system must also be stationary during the duration of the sequence.

Examples

Delta function

Listen

Tds

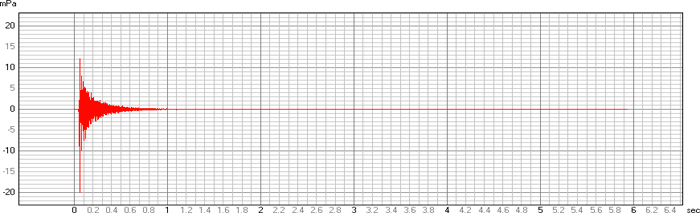
Listen

Mls

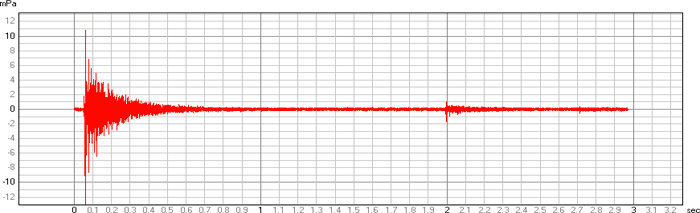
Listen

Basement

• Sound System Measurements using Time Delay Spectrometry
• Impulse Response Measurements Using All-Pass Deconvolution. David Griesinger, Lexicon, Inc. Waltham, Massachusetts 02154, USA
• Introduction to Sound Recording. Geoff Martin, B. Mus., Ph. D., March 14, 2004

PS: there is an interesting site , which is a collection of impulse characteristics of various rooms that are loaded by users. You can also listen to how the vocals or drummers will sound in the room. Unfortunately, the resource has fallen so far. And it is not clear when he will rise.