Leafing through the pages of the hub "Algorithms", I came across a topic dedicated to solving the problem of localizing a point in a polygon: a polygon is defined (a closed polyline without self-intersections), it is necessary to determine whether a given point A is inside this polygon or not. In one of the last comments to the topic, it was puzzled how this purely mathematical task has to do with the theory of algorithms. It has-and, most directly. The task of localization is a classical problem of computational geometry (not to be confused with computer graphics). As a warm-up, you are invited to look at the picture on the right, which shows a polygon of the Peano curve type (source [ 1 ]), and try to answer the question - do you see a red gopher? and I do not see, and he is! is inside or outside the polygon? And below, we (exclusively for educational purposes) will consider a simple variation of this task, when a given polygon is convex.


It is clear that if a polygon is a triangle or a quadrilateral, then there are no algorithms in the full sense of the word, but there are three or four formulas that must be programmed. However, a completely different story begins if the number of vertices of the polygon is large. For example, a million or one hundred million vertices. Such a task seems to be quite an algorithmic one. The naive algorithm (launching a ray from a given point and counting the number of its intersections with the sides of a polygon) is linear in the number of vertices of the polygon n , since we must check the intersection of the ray with all sides of the polygon. Accordingly, the question arises, is it possible to do it faster, i.e. Is there a sublinear algorithm for solving the localization problem in this formulation? The correct answer to this question is yes, the problem can be solved in O (log ₂ n) time. Details of the solution, in the general case when the polygon does not have to be convex, can be found in the excellent book [ 2 ]. And below we will look at how a binary search algorithm can be applied to a point localization problem in a convex polygon.

Small educational program

Let three points A, B, and C be given. Suppose that we look from point A to point B. Where does the point C turn out to be - to the right or left relative to the direction of our view? It is possible to answer this question with the help of the vector product of the vectors a = AB and b = BC, more precisely with the help of the z-coordinate of such a product, which is calculated by the simple formula z = a _x b _y -a _y b _x . If z> 0, then the desired turn is left, if z <0, then right. If the coin fell on the edge z = 0, then the three points lie on one straight line (they say that the vectors a and b are collinear).

Python code that calculates the direction of rotation is elementary (points are represented by lists of length 2):

def rotate(A,B,C): return (B[0]-A[0])*(C[1]-B[1])-(B[1]-A[1])*(C[0]-B[0]) 

With such a useful feature, you can do a lot of good deeds. For example, can one determine if two given segments AB and CD intersect? This, by the way, is another basic operation of computational geometry, and we will also need it soon (though only once). The idea is simple - two segments intersect if and only if the ends of one segment lie on opposite sides of another and vice versa.To check whether the points C and D are located on opposite sides with respect to the segment (vector) AB, one should look at the directions of rotate (A, B, C) and rotate (A, B, D) turns. If the signs of these expressions are different, then the line AB intersects the segment CD (and at the inner point). The signs of two numbers are different, if and only if their product is negative. Therefore, the criterion for the intersection of segments AB and CD is the negativity of two expressions rotate (A, B, C) * rotate (A, B, D) and rotate (C, D, A) * rotate (C, D, B). If we replace strict negativity with nonpositivity, then we will be able to catch the intersection at the end points of the segments. We also need some intermediate version, namely, one product will be weakly compared with zero, the second - strictly:

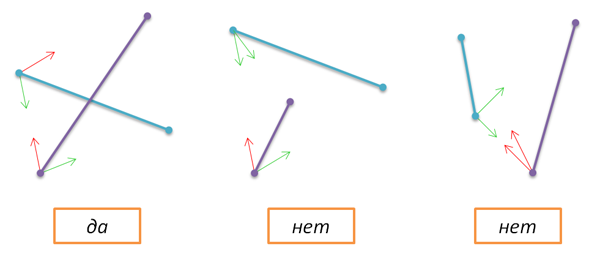
 def intersect(A,B,C,D): return rotate(A,B,C)*rotate(A,B,D)<=0 and rotate(C,D,A)*rotate(C,D,B)<0 

The reason for such a strange choice of inequality signs is a feature of the future application of this function (in particular, points A, B and C will be different vertices of a convex polygon, and point D will be the point we are trying to localize).
')

Binary search

Now we go to the localization itself. Given a convex polygon P consisting of n vertices and a point A. In this case, it is assumed that the vertices in P are numbered counterclockwise (they say that the direction of the walk around the perimeter P is positive).

The idea of ​​the algorithm: take the first vertex of the polygon P ₀ and try to determine which segment (angle) P _i P ₀ P _{i + 1} falls into point A. To begin with, check that A falls into the segment P _n-1 P ₀ P ₁ if this is not the case, then A is guaranteed to lie outside the polygon.

Code:

 def pointloc(P,A): n = len(P) if rotate(P[0],P[1],A)<0 or rotate(P[0],P[n-1],A)>0: return False 

Then everything is as in the classical binary search - we set p = 1, r = n-1 (borders of the current segment), we calculate the average vertex q = (p + r) / 2, we look where A is relative to the vector P ₀ P _q , if on the left, then replace r with q, if on the right, then replace p with q.

We continue this process until it turns out that rp = 1:

  p, r = 1, n-1 while rp>1: q = (p+r)/2 if rotate(P[0],P[q],A)<0: r = q else: p = q 

Now it remains to check whether the segments P ₀ A and P _p P _r intersect?
If they intersect, then point A lies outside, if not intersect, then inside.

Code:

  return not intersect(P[0],A,P[p],P[r]) 

That's all ...

Results

It is easy to verify that the complexity of the algorithm is the same as that of the classical binary search algorithm - O (log ₂ n). And everything would be great if this algorithm was not sharpened under convex polygons. For the sake of fairness, the considered algorithm works with some non-convex polygons, but of a very specific type — in such polygons all diagonals leading from the zero vertex must lie inside the polygon:

The universal localization algorithm also works on the principle of binary search, only inside it everything is arranged, to put it mildly, a bit more complicated.

Thanks for attention!

PS: The task with the picture at the top of the topic is easily solved in any graphic editor: select the fill tool (fill), take a color different from the background, click on the edge of the picture (outside the polygon) and voila!

Literature

1. P. Prusinkiewicz, A. Lindenmayer, The algorithmic beauty of plants , 1996
2. M. de Berg, O. Cheong, M. van Kreveld, M. Overmars, Computational Geometry. Algorithms and Applications , 2008
3. F. Preparata, M. Sheimos, Computational Geometry , 1989