Finger huffman algorithm
You've probably heard about David Huffman and his popular compression algorithm. If not, look for information on the Internet - in this article I will not load you with history or mathematics. Today I just want to try to show you a practical example of applying an algorithm to a character string.
Translator’s note: the author implies a repeating element of the source line - it can be either a character or any bit sequence. Code is not an ASCII or UTF-8 character code, but an encoding sequence of bits.
The source code is attached to the article, which clearly demonstrates how the Huffman algorithm works - it is intended for people who have a poor understanding of the process math. In the future (I hope) I will write an article in which we will talk about applying the algorithm to any files to compress them (that is, let's make a simple archiver like WinRAR or WinZIP).
The idea behind the Huffman coding is based on the frequency of occurrence of a character in a sequence. The symbol that occurs in the sequence most often receives a new very small code, and the symbol that occurs least often receives, on the contrary, a very long code. This is necessary, since we want the whole frequency symbols to occupy the least space (and less than they occupied in the original), and the rarest ones more (but they are rare, it doesn’t matter ). For our program, I decided that the symbol will have a length of 8 bits, that is, it will correspond to the printed character.
')
We could, with the same simplicity, take a 16-bit character (that is, consisting of two characters), as well as 10 bits, 20, and so on. The character size is selected based on the input line, which we expect to meet. For example, if I were going to encode raw video files, I would equate the size of a character to the size of a pixel. Remember that decreasing or increasing the size of a character also changes the code size for each character, because the larger the size, the more characters you can encode with that code size. Combinations of zeros and ones suitable for eight bits are less than sixteen. Therefore, you must choose the size of the character, based on the principle on which the data is repeated in your sequence.
For this algorithm, you will need a minimal understanding of the structure of the binary tree and the priority queue. In the source code, I used the priority queue code from my previous article.
Suppose we have the string “beep boop beer!” For which, in its current form, one byte is spent on each character. This means that the entire string occupies 15 * 8 = 120 bits of memory. After encoding, the string will take 40 bits (in practice, in our program we will output to the console a sequence of 40 zeros and ones representing the coded text bits. To get a real string of 40 bits from them, you need to use bit arithmetic, so today we will not do this).
To better understand the example, we will first do everything manually. The string “beep boop beer!” Is very good for this. To get the code for each symbol based on its frequency, we need to build a binary tree, such that each sheet of this tree will contain a symbol (a printed character from a string). The tree will be built from the leaves to the root, in the sense that symbols with a smaller frequency will be farther from the root than symbols with a larger one. Soon you will see what it is for.
To build a tree, we will use a slightly modified priority queue - the elements with the lowest priority, not the highest, will be the first to be extracted from it. It is necessary to build a tree from the leaves to the root.
First, let's calculate the frequencies of all symbols:
After calculating the frequencies, we will create the nodes of the binary tree for each character and add them to the queue, using the frequency as a priority:

Now we get the first two elements from the queue and link them, creating a new tree node in which both of them will be descendants, and the priority of the new node will be equal to the sum of their priorities. After that we will add the resulting new node back to the queue.

Repeat the same steps and get consistently:

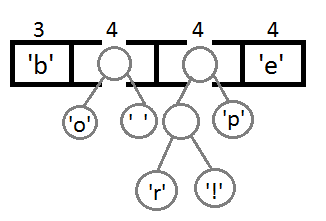
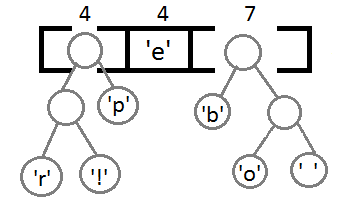

Well, after we link the last two elements, we get the final tree:

Now, to get the code for each character, you just need to walk through the tree, and for each transition add 0 if we go left, and 1 - if right:
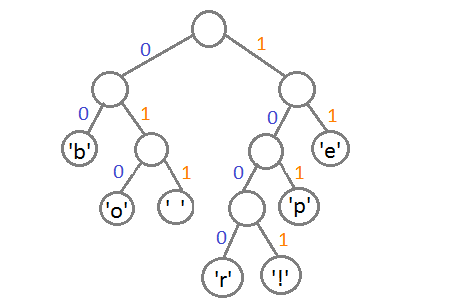
If we do this, we get the following codes for the characters:
To decipher the encoded string, we need, respectively, to simply walk along the tree, turning to the side corresponding to each bit until we reach the leaf. For example, if there is the string “101 11 101 11” and our tree, then we will get the string “pepe”.
It is important to keep in mind that each code is not a prefix for the code of another character. In our example, if 00 is the code for 'b', then 000 cannot be someone's code, because otherwise we will get a conflict. We would never have reached this symbol in the tree, as we would have stayed on 'b'.
In practice, the implementation of this algorithm immediately after building the tree builds a Huffman table. This table is essentially a coherent list or array that contains each character and its code, because it makes coding more efficient. It is quite expensive every time to search for a symbol and simultaneously calculate its code, since we do not know where it is located, and we will have to bypass the entire tree. As a rule, the Huffman table is used for encoding, and the Huffman tree is used for decoding.
Input line: "beep boop beer!"
The input line in binary form: "0110 0010 0110 0101 0110 0101 0111 0000 0010 0000 0110 0010 0110 1111 0110 1111 0111 0000 0010 0000 0110 0010 0110 0101 0110 0101 0111 0010 0010 000"
Encoded string: "0011 1110 1011 0001 0010 1010 1100 1111 1000 1001"
As you can see, there is a big difference between the ASCII version of the string and the encoded version.
The attached source code works on the same principle as described above. In the code you can find more details and comments.
All sources were compiled and tested using the C99 standard. Happy programming!
Download source code
To clarify the situation: this article only illustrates the operation of the algorithm. To use this in real life, you will need to place the Huffman tree you created on a coded string, and the recipient will need to know how to interpret it in order to decode the message. A good way to do this is to walk through the tree in any order that you like (I prefer depth traversal) and concatenate 0 for each node and 1 for a sheet with bits representing the original character (in our case, 8 bits representing ASCII- sign code). It would be ideal to add this representation to the very beginning of the encoded string. Once the recipient builds the tree, he will know how to decode the message to read the original.
Translator’s note: the author implies a repeating element of the source line - it can be either a character or any bit sequence. Code is not an ASCII or UTF-8 character code, but an encoding sequence of bits.
The source code is attached to the article, which clearly demonstrates how the Huffman algorithm works - it is intended for people who have a poor understanding of the process math. In the future (I hope) I will write an article in which we will talk about applying the algorithm to any files to compress them (that is, let's make a simple archiver like WinRAR or WinZIP).
The idea behind the Huffman coding is based on the frequency of occurrence of a character in a sequence. The symbol that occurs in the sequence most often receives a new very small code, and the symbol that occurs least often receives, on the contrary, a very long code. This is necessary, since we want the whole frequency symbols to occupy the least space (and less than they occupied in the original), and the rarest ones more (but they are rare, it doesn’t matter ). For our program, I decided that the symbol will have a length of 8 bits, that is, it will correspond to the printed character.
')
We could, with the same simplicity, take a 16-bit character (that is, consisting of two characters), as well as 10 bits, 20, and so on. The character size is selected based on the input line, which we expect to meet. For example, if I were going to encode raw video files, I would equate the size of a character to the size of a pixel. Remember that decreasing or increasing the size of a character also changes the code size for each character, because the larger the size, the more characters you can encode with that code size. Combinations of zeros and ones suitable for eight bits are less than sixteen. Therefore, you must choose the size of the character, based on the principle on which the data is repeated in your sequence.
For this algorithm, you will need a minimal understanding of the structure of the binary tree and the priority queue. In the source code, I used the priority queue code from my previous article.
Suppose we have the string “beep boop beer!” For which, in its current form, one byte is spent on each character. This means that the entire string occupies 15 * 8 = 120 bits of memory. After encoding, the string will take 40 bits (in practice, in our program we will output to the console a sequence of 40 zeros and ones representing the coded text bits. To get a real string of 40 bits from them, you need to use bit arithmetic, so today we will not do this).
To better understand the example, we will first do everything manually. The string “beep boop beer!” Is very good for this. To get the code for each symbol based on its frequency, we need to build a binary tree, such that each sheet of this tree will contain a symbol (a printed character from a string). The tree will be built from the leaves to the root, in the sense that symbols with a smaller frequency will be farther from the root than symbols with a larger one. Soon you will see what it is for.
To build a tree, we will use a slightly modified priority queue - the elements with the lowest priority, not the highest, will be the first to be extracted from it. It is necessary to build a tree from the leaves to the root.
First, let's calculate the frequencies of all symbols:
| Symbol | Frequency |
|---|---|
| 'b' | 3 |
| 'e' | four |
| 'p' | 2 |
| '' | 2 |
| 'o' | 2 |
| 'r' | one |
| '!' | one |
After calculating the frequencies, we will create the nodes of the binary tree for each character and add them to the queue, using the frequency as a priority:

Now we get the first two elements from the queue and link them, creating a new tree node in which both of them will be descendants, and the priority of the new node will be equal to the sum of their priorities. After that we will add the resulting new node back to the queue.

Repeat the same steps and get consistently:




Well, after we link the last two elements, we get the final tree:

Now, to get the code for each character, you just need to walk through the tree, and for each transition add 0 if we go left, and 1 - if right:

If we do this, we get the following codes for the characters:
| Symbol | Code |
|---|---|
| 'b' | 00 |
| 'e' | eleven |
| 'p' | 101 |
| '' | 011 |
| 'o' | 010 |
| 'r' | 1000 |
| '!' | 1001 |
To decipher the encoded string, we need, respectively, to simply walk along the tree, turning to the side corresponding to each bit until we reach the leaf. For example, if there is the string “101 11 101 11” and our tree, then we will get the string “pepe”.
It is important to keep in mind that each code is not a prefix for the code of another character. In our example, if 00 is the code for 'b', then 000 cannot be someone's code, because otherwise we will get a conflict. We would never have reached this symbol in the tree, as we would have stayed on 'b'.
In practice, the implementation of this algorithm immediately after building the tree builds a Huffman table. This table is essentially a coherent list or array that contains each character and its code, because it makes coding more efficient. It is quite expensive every time to search for a symbol and simultaneously calculate its code, since we do not know where it is located, and we will have to bypass the entire tree. As a rule, the Huffman table is used for encoding, and the Huffman tree is used for decoding.
Input line: "beep boop beer!"
The input line in binary form: "0110 0010 0110 0101 0110 0101 0111 0000 0010 0000 0110 0010 0110 1111 0110 1111 0111 0000 0010 0000 0110 0010 0110 0101 0110 0101 0111 0010 0010 000"
Encoded string: "0011 1110 1011 0001 0010 1010 1100 1111 1000 1001"
As you can see, there is a big difference between the ASCII version of the string and the encoded version.
The attached source code works on the same principle as described above. In the code you can find more details and comments.
All sources were compiled and tested using the C99 standard. Happy programming!
Download source code
To clarify the situation: this article only illustrates the operation of the algorithm. To use this in real life, you will need to place the Huffman tree you created on a coded string, and the recipient will need to know how to interpret it in order to decode the message. A good way to do this is to walk through the tree in any order that you like (I prefer depth traversal) and concatenate 0 for each node and 1 for a sheet with bits representing the original character (in our case, 8 bits representing ASCII- sign code). It would be ideal to add this representation to the very beginning of the encoded string. Once the recipient builds the tree, he will know how to decode the message to read the original.
Source: https://habr.com/ru/post/144200/
All Articles