Entertaining geodesy
Hello!
Today I will tell you,% USERNAME%, aboutshoes and sealing wax, cabbage, kings, coordinates, projections, geodesic systems, and just a little bit about web cartography. Get comfortable.
As Arthur Clark said, any sufficiently advanced technology is indistinguishable from magic. So in web-cartography - I think everyone has long been used to using geographical maps, but not everyone imagines how this all works.
Here, it would seem, a simple thing - geographical coordinates. Latitude and longitude, what could be easier. But imagine that you find yourself on a desert island. The smartphone drowned, and you have no other means of communication. It remains only to write a letter asking for help and throw it into the sea in a sealed bottle in the old-fashioned way.
')
That's just bad luck - you absolutely do not know where your uninhabited island is, and without specifying the coordinates, no one will find you, even if they catch your letter. What to do? How to determine the coordinates without GPS?
So, a little theory to begin with. In order to compare coordinates to points on the surface of a sphere, it is necessary to specify a reference point — the fundamental plane for counting latitudes and the zero meridian for counting longitudes. For the Earth, the equatorial plane and the Greenwich meridian are usually used, respectively.
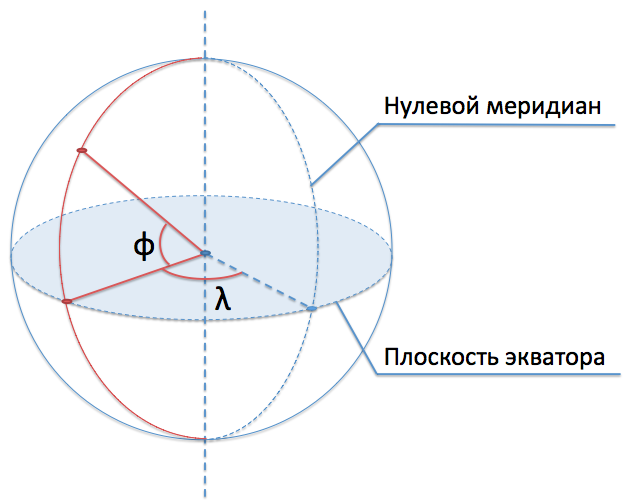
Width (usually denoted by φ) is the angle between the direction to a point from the center of the sphere and the fundamental plane. Longitude (usually denoted by θ or λ) is the angle between the plane of the meridian passing through a point and the plane of the zero meridian.
How to determine its latitude, i.e. the angle between the plane of the earth's equator and the point at which you are?
Let's look at the same drawing from a different angle, projecting it onto the plane of our meridian. Also add to the drawing the plane of the horizon (the tangent plane to our point):
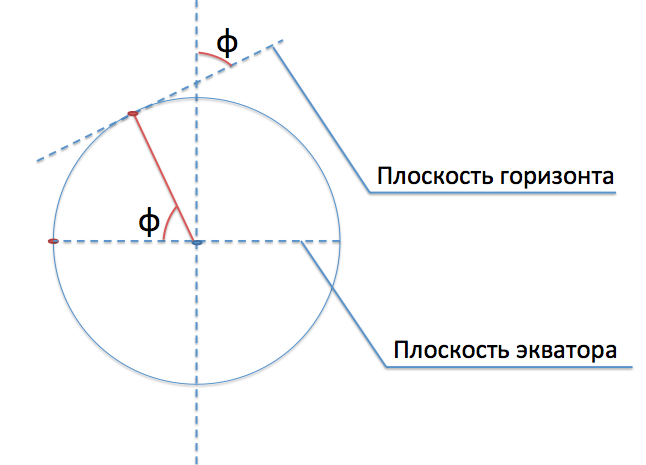
We see that the desired angle between the direction to a point and the equatorial plane is equal to the angle between the horizon plane and the axis of rotation of the Earth.
So, how do we find this angle? Recall the beautiful pictures of the starry sky with a long exposure:
This point in the center of all circles described by stars is the pole of the world. Measuring its height above the horizon, we obtain the latitude of the observation point.
The question remains how to find the pole of the world in the starry sky. If you're in the Northern Hemisphere, then everything is pretty simple:
- Locate the dipper bucket;
- mentally draw a straight through two extreme stars of the dipper - Dubhe and Merak;
- This line will point you to the handle of the bucket Ursa Minor. The extreme star of this pen, the Polar, almost coincides with the North Pole of the world.
The polar star is always in the north, and its height above the horizon is equal to the latitude of the observation point. If you get to the North Pole, the North Star will be right over your head.
Things are not so simple in the southern hemisphere. There are no major stars near the south pole of the world, and you will have to find the Southern Cross constellation, mentally extend its larger crossbar and count 4.5 of its length - somewhere in this area there will be the South Pole of the world.
The constellation itself is easy to find - you have seen it many times on the flags of different countries - Australia, New Zealand and Brazil, for example.
Determined with latitude. Go to the longitude. How to determine the longitude on a desert island?
In fact, this is a very difficult problem, because, in contrast to latitude, the starting point of longitude (zero meridian) is chosen arbitrarily and is not tied to any observed landmarks. The Spanish king Philip II in 1567 appointed a solid reward to those who propose a method for determining longitude; in 1598, under Philip III, it grew to 6,000 ducats at a time and 2,000 rent ducats for life — a very decent amount for those times. The task of determining longitude for several decades was the idea of fixing mathematicians, like Fermat's theorem in the 20th century.
As a result, they began to determine the longitude with the help of this device:
In fact, this device remains the most reliable way to determine longitude (not counting GPS / Glonass) even today. This device ... (drum roll) ... marine chronometer.
In fact, when longitude changes, the time zone changes. The difference in local time and Greenwich is easy to determine its own longitude, and very accurately. Each minute of time difference corresponds to 15 angular minutes of longitude.
Accordingly, if you have a clock set in Greenwich time (in fact, no matter for what - it is enough to know the time zone of the place in which your watch runs) - do not rush to transfer them. Wait for the local half day, and the time difference will tell you the length of your island. (It is very easy to determine the noon time - watch the shadows. In the first half of the day the shadows are shortened, in the second - they lengthen. The moment when the shadows began to lengthen - an astronomical afternoon in the area.)
Both methods of determining the coordinates, by the way, are well described in Jules Verne’s novel The Mysterious Island.
So, we were able to determine our latitude and longitude with an error of several degrees, i.e. a couple of hundred kilometers. For a note in a bottle, this accuracy may be enough, but for geographic maps there is no longer.
In part, this error is due to the imperfection of the tools used, but there are other sources of error. Earth can be considered a ball only as a first approximation - in general, the Earth is not a ball at all, but a geoid is a body most similar to a strongly uneven ellipsoid of rotation. In order to accurately assign coordinates to each point on the earth's surface, we need rules — how to project a specific point on the geoid onto a sphere.
Such a set of rules should be universal for all geographical maps in the world - otherwise the same coordinates in different systems will denote different points of the earth's surface. Currently, almost all geographic services use a unified system of assignment to a point of coordinates - WGS 84 (WGS = World Geodetic System, 84 is the year of adoption of the standard).
WGS 84 defines a so-called. reference ellipsoid - surface, to which coordinates are brought for convenience of calculations. The parameters of this ellipsoid are as follows:
- semi-major axis (equatorial radius): a = 6378137 meters;
- compression: f = 1 / 298.257223563.
From the equatorial radius and compression, the polar radius can be obtained, it is also a small semi-axis (b = a * (1 - f) ≈ 6356752 meters).
Any point on the earth's surface, therefore, is assigned three coordinates: longitude and latitude (on the reference ellipsoid) and height above its surface. In 2004, the WGS 84 was complemented by the Earth Gravitational Model (EGM96) standard, which specifies the sea level from which heights are calculated.
Interestingly, the zero meridian in WGS 84 is not at all Greenwich (passing through the axis of the transit instrument of the Greenwich Observatory), but the so-called. IERS Reference Meridian, which runs at 5.31 angular seconds east of Greenwich.
Suppose we learned to determine their coordinates. Now you need to learn how to display the accumulated geographical knowledge of the monitor screen. Why, bad luck - there are somehow not very many spherical monitors in the world (not to mention geoid monitors). We need to somehow map the map onto a plane — project it.
One of the easiest ways is to project a sphere onto a cylinder, and then turn this cylinder onto a plane. Such projections are called cylindrical; their characteristic property is that all meridians are displayed on the map by vertical lines.
Projections of the sphere on the cylinder can come up with a lot. The most famous of the cylindrical projections is the Mercator projection (by the name of the Flemish cartographer and geographer Gerard Kremer who used it widely in her maps, better known by the Latinized name Mercator).
Mathematically, it is expressed as follows (for a sphere):
x = R · λ;
y = R · ln (tg (π / 4 + φ / 2), where R is the radius of the sphere, λ is the longitude in radians, φ is the latitude in radians.
At the output we get the usual Cartesian coordinates in meters.
A map in the Mercator projection looks like this:
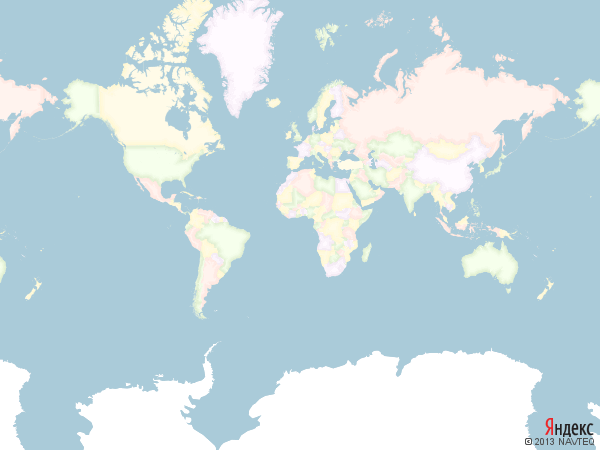
It is easy to see that the Mercator projection distorts the shapes and areas of objects very significantly. For example, Greenland on the map is twice as large as Australia - although in reality Australia is 3.5 times as large as Greenland.
Why is this projection so good that it has become so popular despite significant distortions? The fact is that the Mercator projection has an important characteristic property: it retains angles when projecting.
Suppose we want to sail from the Canary Islands to the Bahamas. Let's draw a straight line on the map connecting the points of departure and arrival.
Since all the meridians in cylindrical projections are parallel, and the Mercator projection also preserves the angles, our line will cross all the meridians at the same angle. And this means that it will be very simple to swim along this line: it is enough to keep the same angle between the ship’s course and the direction of the polar star (or the direction of magnetic north, which is less accurate) throughout the journey, and you can easily measure banal protractor.
Similar lines crossing all the meridians and parallels at the same angle are called loxodromes. All loxodromes in the Mercator projection are depicted as straight lines on the map, and it is this remarkable property, extremely convenient for marine navigation, that brought the Mercator projection to widespread popularity among sailors.
It should be noted that what has been said is not quite true: if we project the sphere and move along the geoid, then the track angle will be determined not quite correctly and we will not quite sail there. (The discrepancy can be quite noticeable - after all, the equatorial and polar radii of the Earth differ by more than 20 kilometers.) The ellipsoid can also be projected with the angles preserved, although the formulas for the elliptical Mercator projection are much more complicated than for the spherical (the inverse transformation is not expressed at all in elementary functions). A complete and detailed description of the mathematics of the Mercator projection on the ellipsoid can be found here .
When we in Yandex started making our cards, it seemed logical to us to use an elliptical Mercator projection. Unfortunately, many other web-mapping services didn’t seem that way, and they use a spherical projection. Therefore, for a long time, it was impossible to show tiles on top of the Yandex map, say, OSM - they diverged along the y axis, the closer to the pole - the more noticeable. In the version of API 2.0, we decided not to swim against the stream, and provided the opportunity to work with the map in any projection, and to show on the map several layers simultaneously in different projections - as convenient.
Traveling around the loxodrome is very simple, but you have to pay for this simplicity: the loxodrome will send you on a trip along a non-optimal route. In particular, the path along the parallel (if it is not the equator) is not the shortest!
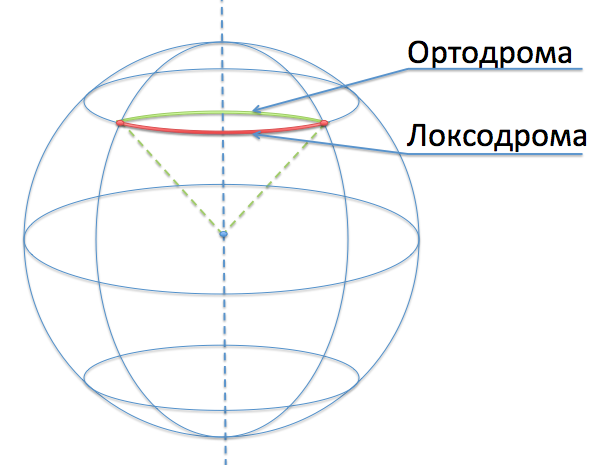
In order to find the shortest path on a sphere, one must draw a circle with the center in the center of the sphere, passing through these two points (or, equivalently, to cross the sphere with the plane passing through two points and the center of the sphere).
It is impossible to project a sphere onto a plane so that the shortest paths thus go into straight line segments; The Mercator projection, of course, is no exception, and the orthodroms in it look like highly distorted arcs. Some paths (through the pole) in the Mercator projection cannot be correctly depicted:
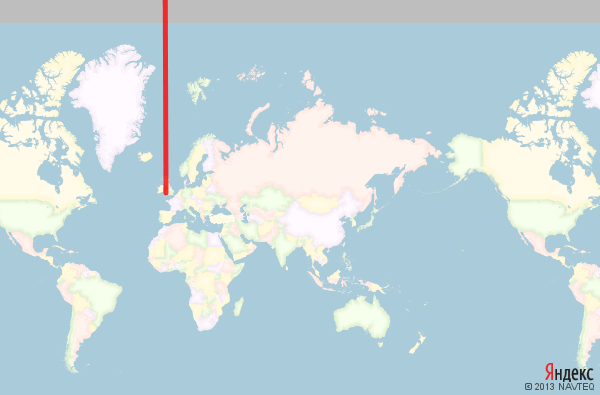
Approximately, the shortest path from Anadyr to Cardiff is projected: first, we fly away to infinity strictly to the north, and then return from infinity to the south.
In the case of movement along a sphere, the shortest paths are constructed quite simply with the aid of a spherical trigonometry apparatus, but in the case of an ellipsoid, the task is significantly complicated - the shortest paths are not expressed in elementary functions.
(I note that this problem, of course, is not solved by choosing a spherical Mercator projection - the construction of the shortest paths is carried out on the WGS 84 reference ellipsoid and does not depend on the projection parameters.)
During the development of the Yandex.Map API version 2.0, we faced a difficult task - to parameterize the construction of the shortest paths so that:
- it was easy to use the built-in functions for calculating the shortest paths on the WGS 84 ellipsoid;
- it was easy to set your own coordinate system with your own methods for calculating the shortest paths.
The Maps API can be used not only to display maps of the earth’s surface, but also, say, the surface of the moon or some game world.
In order to build the shortest paths (geodesic lines) in the general case, the following simple and simple equation is used:
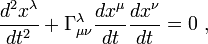
Here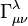
- so-called Christoffel symbols expressed in partial derivatives of the fundamental metric tensor.
It seemed to us to be somewhat inhuman to force the user in such a way to parameterize his mapping area :).
Therefore, we decided to go another way, more close to the Earth and the needs of our users. In geodesy, the problems of constructing shortest paths are so-called. the first (direct) and second (inverse) geodetic tasks.
Direct geodesic task: the starting point is given, the direction of movement (usually the track angle, that is, the angle between the north direction and the direction of movement) and the distance traveled. It is required to find the end point and the final direction of motion.
Inverse geodetic problem: two points are given. It is required to find the distance between them and the direction of motion.
Note that the direction of travel (track angle) is a continuous function that changes throughout the journey.
Having at our disposal the functions of solving these problems, we can solve the cases we need in the Maps API: calculating distances, displaying the shortest paths and constructing circles on the earth's surface.
We have declared the following interface for user coordinate systems:
solveDirectProblem (startPoint, direction, distance) - Solves the so-called first (direct) geodesic task: where we find ourselves, if we leave the specified point in the specified direction and pass, without turning, the specified distance.
solveInverseProblem (startPoint, endPoint, reverseDirection) - Solves the so-called second (reverse) geodesic task: build the shortest route between two points on the mapped surface and determine the distance and direction of motion.
getDistance (point1, point2) - returns the shortest (along the geodesic line) distance between two given points (in meters).
(The function getDistance is allocated separately for those cases where the calculation of distances can be performed much faster than the solution of the inverse problem.)
This interface seemed simple enough for us to implement in cases where the user mapped some nonstandard surface or uses nonstandard coordinates. For our part, we wrote two standard implementations — for the conventional Cartesian plane and for the reference ellipsoid WGS 84. For the second implementation, we used the Vincenti formulas . By the way, I directly implemented this logic of runawayed , we say hello to it :).
All these geodesic features are available in the Yandex.Maps API, starting with version 2.0.13. Welcome!
Today I will tell you,% USERNAME%, about
As Arthur Clark said, any sufficiently advanced technology is indistinguishable from magic. So in web-cartography - I think everyone has long been used to using geographical maps, but not everyone imagines how this all works.
Here, it would seem, a simple thing - geographical coordinates. Latitude and longitude, what could be easier. But imagine that you find yourself on a desert island. The smartphone drowned, and you have no other means of communication. It remains only to write a letter asking for help and throw it into the sea in a sealed bottle in the old-fashioned way.
')
That's just bad luck - you absolutely do not know where your uninhabited island is, and without specifying the coordinates, no one will find you, even if they catch your letter. What to do? How to determine the coordinates without GPS?
So, a little theory to begin with. In order to compare coordinates to points on the surface of a sphere, it is necessary to specify a reference point — the fundamental plane for counting latitudes and the zero meridian for counting longitudes. For the Earth, the equatorial plane and the Greenwich meridian are usually used, respectively.
Width (usually denoted by φ) is the angle between the direction to a point from the center of the sphere and the fundamental plane. Longitude (usually denoted by θ or λ) is the angle between the plane of the meridian passing through a point and the plane of the zero meridian.
How to determine its latitude, i.e. the angle between the plane of the earth's equator and the point at which you are?
Let's look at the same drawing from a different angle, projecting it onto the plane of our meridian. Also add to the drawing the plane of the horizon (the tangent plane to our point):
We see that the desired angle between the direction to a point and the equatorial plane is equal to the angle between the horizon plane and the axis of rotation of the Earth.
So, how do we find this angle? Recall the beautiful pictures of the starry sky with a long exposure:
This point in the center of all circles described by stars is the pole of the world. Measuring its height above the horizon, we obtain the latitude of the observation point.
The question remains how to find the pole of the world in the starry sky. If you're in the Northern Hemisphere, then everything is pretty simple:
- Locate the dipper bucket;
- mentally draw a straight through two extreme stars of the dipper - Dubhe and Merak;
- This line will point you to the handle of the bucket Ursa Minor. The extreme star of this pen, the Polar, almost coincides with the North Pole of the world.
The polar star is always in the north, and its height above the horizon is equal to the latitude of the observation point. If you get to the North Pole, the North Star will be right over your head.
Things are not so simple in the southern hemisphere. There are no major stars near the south pole of the world, and you will have to find the Southern Cross constellation, mentally extend its larger crossbar and count 4.5 of its length - somewhere in this area there will be the South Pole of the world.
The constellation itself is easy to find - you have seen it many times on the flags of different countries - Australia, New Zealand and Brazil, for example.
Determined with latitude. Go to the longitude. How to determine the longitude on a desert island?
In fact, this is a very difficult problem, because, in contrast to latitude, the starting point of longitude (zero meridian) is chosen arbitrarily and is not tied to any observed landmarks. The Spanish king Philip II in 1567 appointed a solid reward to those who propose a method for determining longitude; in 1598, under Philip III, it grew to 6,000 ducats at a time and 2,000 rent ducats for life — a very decent amount for those times. The task of determining longitude for several decades was the idea of fixing mathematicians, like Fermat's theorem in the 20th century.
As a result, they began to determine the longitude with the help of this device:
In fact, this device remains the most reliable way to determine longitude (not counting GPS / Glonass) even today. This device ... (drum roll) ... marine chronometer.
In fact, when longitude changes, the time zone changes. The difference in local time and Greenwich is easy to determine its own longitude, and very accurately. Each minute of time difference corresponds to 15 angular minutes of longitude.
Accordingly, if you have a clock set in Greenwich time (in fact, no matter for what - it is enough to know the time zone of the place in which your watch runs) - do not rush to transfer them. Wait for the local half day, and the time difference will tell you the length of your island. (It is very easy to determine the noon time - watch the shadows. In the first half of the day the shadows are shortened, in the second - they lengthen. The moment when the shadows began to lengthen - an astronomical afternoon in the area.)
Both methods of determining the coordinates, by the way, are well described in Jules Verne’s novel The Mysterious Island.
Geoid coordinates
So, we were able to determine our latitude and longitude with an error of several degrees, i.e. a couple of hundred kilometers. For a note in a bottle, this accuracy may be enough, but for geographic maps there is no longer.
In part, this error is due to the imperfection of the tools used, but there are other sources of error. Earth can be considered a ball only as a first approximation - in general, the Earth is not a ball at all, but a geoid is a body most similar to a strongly uneven ellipsoid of rotation. In order to accurately assign coordinates to each point on the earth's surface, we need rules — how to project a specific point on the geoid onto a sphere.
Such a set of rules should be universal for all geographical maps in the world - otherwise the same coordinates in different systems will denote different points of the earth's surface. Currently, almost all geographic services use a unified system of assignment to a point of coordinates - WGS 84 (WGS = World Geodetic System, 84 is the year of adoption of the standard).
WGS 84 defines a so-called. reference ellipsoid - surface, to which coordinates are brought for convenience of calculations. The parameters of this ellipsoid are as follows:
- semi-major axis (equatorial radius): a = 6378137 meters;
- compression: f = 1 / 298.257223563.
From the equatorial radius and compression, the polar radius can be obtained, it is also a small semi-axis (b = a * (1 - f) ≈ 6356752 meters).
Any point on the earth's surface, therefore, is assigned three coordinates: longitude and latitude (on the reference ellipsoid) and height above its surface. In 2004, the WGS 84 was complemented by the Earth Gravitational Model (EGM96) standard, which specifies the sea level from which heights are calculated.
Interestingly, the zero meridian in WGS 84 is not at all Greenwich (passing through the axis of the transit instrument of the Greenwich Observatory), but the so-called. IERS Reference Meridian, which runs at 5.31 angular seconds east of Greenwich.
Flat cards
Suppose we learned to determine their coordinates. Now you need to learn how to display the accumulated geographical knowledge of the monitor screen. Why, bad luck - there are somehow not very many spherical monitors in the world (not to mention geoid monitors). We need to somehow map the map onto a plane — project it.
One of the easiest ways is to project a sphere onto a cylinder, and then turn this cylinder onto a plane. Such projections are called cylindrical; their characteristic property is that all meridians are displayed on the map by vertical lines.
Projections of the sphere on the cylinder can come up with a lot. The most famous of the cylindrical projections is the Mercator projection (by the name of the Flemish cartographer and geographer Gerard Kremer who used it widely in her maps, better known by the Latinized name Mercator).
Mathematically, it is expressed as follows (for a sphere):
x = R · λ;
y = R · ln (tg (π / 4 + φ / 2), where R is the radius of the sphere, λ is the longitude in radians, φ is the latitude in radians.
At the output we get the usual Cartesian coordinates in meters.
A map in the Mercator projection looks like this:
It is easy to see that the Mercator projection distorts the shapes and areas of objects very significantly. For example, Greenland on the map is twice as large as Australia - although in reality Australia is 3.5 times as large as Greenland.
Why is this projection so good that it has become so popular despite significant distortions? The fact is that the Mercator projection has an important characteristic property: it retains angles when projecting.
Suppose we want to sail from the Canary Islands to the Bahamas. Let's draw a straight line on the map connecting the points of departure and arrival.
Since all the meridians in cylindrical projections are parallel, and the Mercator projection also preserves the angles, our line will cross all the meridians at the same angle. And this means that it will be very simple to swim along this line: it is enough to keep the same angle between the ship’s course and the direction of the polar star (or the direction of magnetic north, which is less accurate) throughout the journey, and you can easily measure banal protractor.
Similar lines crossing all the meridians and parallels at the same angle are called loxodromes. All loxodromes in the Mercator projection are depicted as straight lines on the map, and it is this remarkable property, extremely convenient for marine navigation, that brought the Mercator projection to widespread popularity among sailors.
It should be noted that what has been said is not quite true: if we project the sphere and move along the geoid, then the track angle will be determined not quite correctly and we will not quite sail there. (The discrepancy can be quite noticeable - after all, the equatorial and polar radii of the Earth differ by more than 20 kilometers.) The ellipsoid can also be projected with the angles preserved, although the formulas for the elliptical Mercator projection are much more complicated than for the spherical (the inverse transformation is not expressed at all in elementary functions). A complete and detailed description of the mathematics of the Mercator projection on the ellipsoid can be found here .
When we in Yandex started making our cards, it seemed logical to us to use an elliptical Mercator projection. Unfortunately, many other web-mapping services didn’t seem that way, and they use a spherical projection. Therefore, for a long time, it was impossible to show tiles on top of the Yandex map, say, OSM - they diverged along the y axis, the closer to the pole - the more noticeable. In the version of API 2.0, we decided not to swim against the stream, and provided the opportunity to work with the map in any projection, and to show on the map several layers simultaneously in different projections - as convenient.
Geodetic tasks
Traveling around the loxodrome is very simple, but you have to pay for this simplicity: the loxodrome will send you on a trip along a non-optimal route. In particular, the path along the parallel (if it is not the equator) is not the shortest!
In order to find the shortest path on a sphere, one must draw a circle with the center in the center of the sphere, passing through these two points (or, equivalently, to cross the sphere with the plane passing through two points and the center of the sphere).
It is impossible to project a sphere onto a plane so that the shortest paths thus go into straight line segments; The Mercator projection, of course, is no exception, and the orthodroms in it look like highly distorted arcs. Some paths (through the pole) in the Mercator projection cannot be correctly depicted:
Approximately, the shortest path from Anadyr to Cardiff is projected: first, we fly away to infinity strictly to the north, and then return from infinity to the south.
In the case of movement along a sphere, the shortest paths are constructed quite simply with the aid of a spherical trigonometry apparatus, but in the case of an ellipsoid, the task is significantly complicated - the shortest paths are not expressed in elementary functions.
(I note that this problem, of course, is not solved by choosing a spherical Mercator projection - the construction of the shortest paths is carried out on the WGS 84 reference ellipsoid and does not depend on the projection parameters.)
During the development of the Yandex.Map API version 2.0, we faced a difficult task - to parameterize the construction of the shortest paths so that:
- it was easy to use the built-in functions for calculating the shortest paths on the WGS 84 ellipsoid;
- it was easy to set your own coordinate system with your own methods for calculating the shortest paths.
The Maps API can be used not only to display maps of the earth’s surface, but also, say, the surface of the moon or some game world.
In order to build the shortest paths (geodesic lines) in the general case, the following simple and simple equation is used:
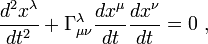
Here
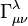- so-called Christoffel symbols expressed in partial derivatives of the fundamental metric tensor.
It seemed to us to be somewhat inhuman to force the user in such a way to parameterize his mapping area :).
Therefore, we decided to go another way, more close to the Earth and the needs of our users. In geodesy, the problems of constructing shortest paths are so-called. the first (direct) and second (inverse) geodetic tasks.
Direct geodesic task: the starting point is given, the direction of movement (usually the track angle, that is, the angle between the north direction and the direction of movement) and the distance traveled. It is required to find the end point and the final direction of motion.
Inverse geodetic problem: two points are given. It is required to find the distance between them and the direction of motion.
Note that the direction of travel (track angle) is a continuous function that changes throughout the journey.
Having at our disposal the functions of solving these problems, we can solve the cases we need in the Maps API: calculating distances, displaying the shortest paths and constructing circles on the earth's surface.
We have declared the following interface for user coordinate systems:
solveDirectProblem (startPoint, direction, distance) - Solves the so-called first (direct) geodesic task: where we find ourselves, if we leave the specified point in the specified direction and pass, without turning, the specified distance.
solveInverseProblem (startPoint, endPoint, reverseDirection) - Solves the so-called second (reverse) geodesic task: build the shortest route between two points on the mapped surface and determine the distance and direction of motion.
getDistance (point1, point2) - returns the shortest (along the geodesic line) distance between two given points (in meters).
(The function getDistance is allocated separately for those cases where the calculation of distances can be performed much faster than the solution of the inverse problem.)
This interface seemed simple enough for us to implement in cases where the user mapped some nonstandard surface or uses nonstandard coordinates. For our part, we wrote two standard implementations — for the conventional Cartesian plane and for the reference ellipsoid WGS 84. For the second implementation, we used the Vincenti formulas . By the way, I directly implemented this logic of runawayed , we say hello to it :).
All these geodesic features are available in the Yandex.Maps API, starting with version 2.0.13. Welcome!
Source: https://habr.com/ru/post/143898/
All Articles