On the use of entropy to identify texts
One of the practical problems faced by the theory of information is the question of the identification of texts and the definition of authorship. Let us study one of the possible ways to solve this problem, based on the measurement and comparison of the entropy indicators of this and reference texts for the problem of determining the identity of a piece of text.
Usually, the entropy of the Markov process is used for comparing texts and determining authorship, which shows the average amount of information in bits, which is reported by one character if k – 1 is known. After reviewing some of these works, which did not take into account that the compared works have a different volume, I decided to study the dependence of the text entropy on its volume.
Of the six texts of three authors, samples of various volumes were made and the average entropy values were calculated from 1 to 6 orders of magnitude inclusive. The results of the work can be seen in the graphs (the upper lines correspond to the entropy of the first order, the lower ones - 6):
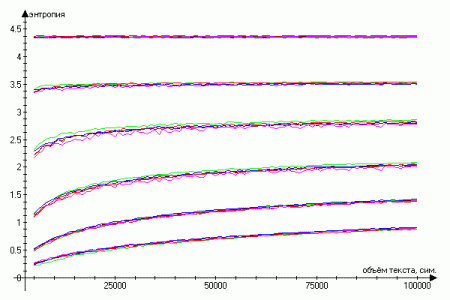
Thus, the higher the order, the stronger the logarithmic dependence of the entropy on the volume of the text. And already for the second order with given samples, the logarithmic trend explains on average 85% of the variance, when considering volumes of less than 50 thousand sunflowers - more than 90%. This means that the first-order entropy, that is, the distribution of frequencies of individual characters without taking into account their sequences, is the most stable and independent of the length of the text.
A more detailed consideration of the first-order entropy can be seen that for a volume of less than 30 thousand characters the average entropy is less than the entropy of the whole text, but the general relations remain (the dotted line shows the entropy of the whole text)

It can be seen that the graphs overlap, which already indicates that it is impossible to unambiguously determine the ownership of the text at the intersection points.
However, to answer the question about the solvability of our problem, it is necessary to estimate the spread of values within one text. In the following graph, all intermediate samples are shown in dots. The resulting fluctuation of entropy within one text exceeds the difference between the average values, which indicates the impossibility of an exact solution of the problem of a text fragment belonging under these conditions.

Thus, the method based on direct comparison of the entropy of the text-fragment and the reference text is extremely inaccurate and is not suitable for identifying texts because of the large scatter of values within the text. Unlike characteristics based on the number of N-grams and direct comparison of the relative frequencies of their distribution, entropy is an impersonal parameter and its use in exact problems can lead to errors.
Usually, the entropy of the Markov process is used for comparing texts and determining authorship, which shows the average amount of information in bits, which is reported by one character if k – 1 is known. After reviewing some of these works, which did not take into account that the compared works have a different volume, I decided to study the dependence of the text entropy on its volume.
Of the six texts of three authors, samples of various volumes were made and the average entropy values were calculated from 1 to 6 orders of magnitude inclusive. The results of the work can be seen in the graphs (the upper lines correspond to the entropy of the first order, the lower ones - 6):

Thus, the higher the order, the stronger the logarithmic dependence of the entropy on the volume of the text. And already for the second order with given samples, the logarithmic trend explains on average 85% of the variance, when considering volumes of less than 50 thousand sunflowers - more than 90%. This means that the first-order entropy, that is, the distribution of frequencies of individual characters without taking into account their sequences, is the most stable and independent of the length of the text.
A more detailed consideration of the first-order entropy can be seen that for a volume of less than 30 thousand characters the average entropy is less than the entropy of the whole text, but the general relations remain (the dotted line shows the entropy of the whole text)

It can be seen that the graphs overlap, which already indicates that it is impossible to unambiguously determine the ownership of the text at the intersection points.
However, to answer the question about the solvability of our problem, it is necessary to estimate the spread of values within one text. In the following graph, all intermediate samples are shown in dots. The resulting fluctuation of entropy within one text exceeds the difference between the average values, which indicates the impossibility of an exact solution of the problem of a text fragment belonging under these conditions.

Thus, the method based on direct comparison of the entropy of the text-fragment and the reference text is extremely inaccurate and is not suitable for identifying texts because of the large scatter of values within the text. Unlike characteristics based on the number of N-grams and direct comparison of the relative frequencies of their distribution, entropy is an impersonal parameter and its use in exact problems can lead to errors.
')
Source: https://habr.com/ru/post/14389/
All Articles