About AI in Mind Games
Not so long ago, I became interested in playing shogi. Unfortunately, this wonderful game is practically unknown in Russia, so until I taught friends to play, I had to play with the program. Of course, I was wondering how this program works.
Below is a short story about computer algorithms used in intellectual games.
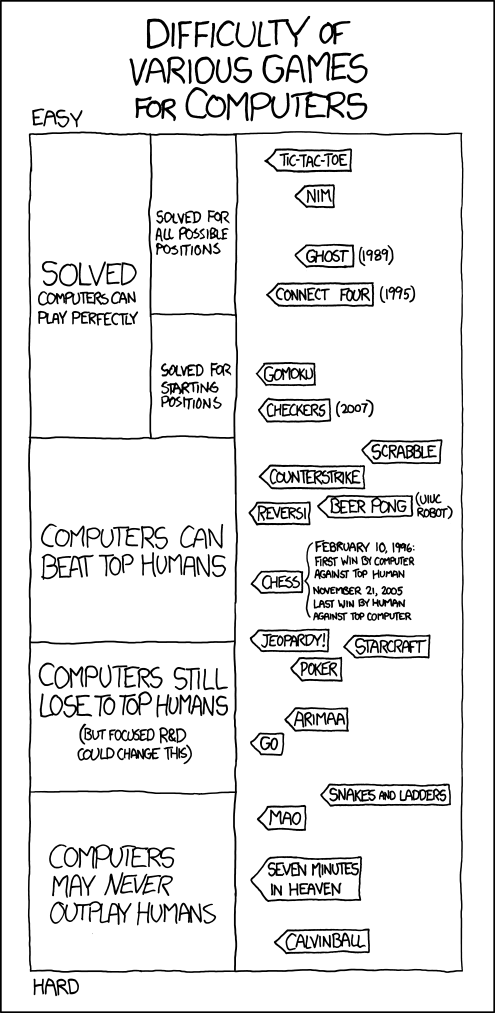
We begin the consideration of algorithms with one of the most simple games: with daggers and crosses. I'm sure almost all of you can play in such a way that you never lose, but let's see how a computer does it.
Almost all games can be represented as a so-called. decision trees, where each node will represent one step of solving the problem (a move in the game), a branch in the tree corresponds to a solution that leads to a more complete solution, the sheets represent the final solution (final positions). Our goal is to find in the tree the best way from root to leaf.
Decision trees are usually incredibly large. For the tic-tac-toe game we are considering, the tree contains more than half a million knots. It is clear that in checkers, chess, and especially segah and go, trees are much more.
But, nevertheless, using the example of a children's game, one can consider methods that allow one to find optimal solutions in very large trees.
If a player has n possible moves, then the corresponding node will have n branches (descendants). For example, in noughts and crosses, the root node corresponds to an empty field. The first player can put a cross on any of the 9 squares. Each possible move will correspond to a branch originating from the root node. When a player has put a cross, the second player can place a zero in any of the remaining eight squares. Each of these moves corresponds to a branch originating from the node representing the current position of the cross on the board. The figure shows a small fragment of the tree under study.

As you can see from the picture, the game tree is growing extremely fast. If the tree continues to grow in this way, then the whole tree will contain 9! = 362880 leaves.
In fact, many possible nodes in the game tree are prohibited by the rules. For example, if one of the players has already won, then the tree can be completed at this stage. Removing all impossible nodes will reduce the tree to a quarter of a million sheets. But it is still a very, very large tree and it will take an inadmissibly long time to complete it. For more complex games, trees are simply unimaginable size. If in chess at each step the player would have 16 possible moves, there would be more than a trillion nodes in the tree after five moves.
To perform a search in the game tree, you need to be able to determine the value of the position of the playing field. In the tic-tac-toe for the first player, the positions in which the three crosses are arranged in a row are important, since the first player wins. The value of the player who puts a zero in these positions is very small, because at the same time he loses.
Each player can be assigned four values for a specific position on the field:
• 4 - winning;
• 3 - not clear situation;
• 2 - draw;
• 1 - loss;
For an exhaustive study of the game tree, you can use the minimax strategy. In doing so, we will try to minimize the maximum value that a position can have for an opponent after the next move. First, the maximum value that the opponent can dial after each of your possible moves is determined. Then the turn is chosen, at which the opponent gets the minimum value.
The procedure of finding the optimal course calculates the value of the field position. This procedure explores every possible move. For each move, she recursively calls herself to determine the value that the position of the opponent will have. Then she chooses a move that gives the opponent a minimum value. The recursive treatment of the procedure to yourself will continue until one of the three possible events occurs. First, the position in which the player wins can be found. In this case, the procedure sets the field position value to 4. In case the player loses, the field value will be set to 1. Secondly, a position in which no player can make a move can be found. The game ends in a draw, so the procedure sets the position to 2. And finally, the procedure can achieve a predetermined recursion depth. If it exceeds the allowable depth, then the field value is set to 3, indicating an indefinite outcome. The maximum recursion depth prevents the program from spending too much time. This is especially important for complex games, like chess, where the search can last for almost infinitely long time. The maximum recursion depth also allows you to set the skill level. The deeper a program can explore a tree, the better its moves will be.
The picture shows the game tree at the end of the game. The first and third moves lead to the victory of the player playing with zeros, so these moves have the value 4 for him. The second possible move leads to a draw and has the value 2. The program chooses the second move, because it gives the player the zeroes the smallest field value.

')
If the minimax algorithm would be the only tool for the study of game trees, then the search of large trees would be quite difficult. Fortunately, there are several techniques that you can use to search in large trees.
First, you can remember the first few moves chosen by the game experts. If you select the first move for the program, the search tree will be reduced by 9 times. In fact, the program should not go through the tree until the opponent has made a move. In this case, both the computer and his opponent have already chosen branches, therefore the tree will contain only 7! = 5040 branches.
Using additional memory to store multiple moves significantly reduces the time required to search the tree.
Another way to improve the search is to specify important patterns. In chess, such patterns can be positions that threaten several pieces at once, the king or the queen. In case the chess program notices the exchange pattern, it can temporarily change the depth of the recursion to view the series of exchanges to the end and decide whether the exchange will be beneficial. If the exchange does occur, the number of the remaining figures becomes smaller and the search in the tree is simplified.
And, finally, in more complex cases it is necessary to use heuristics. For example, in chess, the usual heuristic is gain advantage. When your opponent has fewer strong pieces and the same number of weak pieces with you, you should go for an exchange whenever possible.
Even a schoolboy can completely bust a tree in noughts and crosses. In checkers, the number of possible positions is estimated to be 10 20 . This is very, very much, but in 2007 the supercomputer was able to calculate all possible moves. That is, since 2007, a person cannot (even theoretically) win over a computer.
With chess, brute force is hardly possible in the near future. The number of all possible positions in chess is estimated by the number 10 46 . This number is so large that even a supercomputer will need astronomical time to sort through these positions. Nevertheless, in chess there is a certain progress. It’s impossible to go through all the positions, but heuristics and position bases are very effective. If you ever learned to play chess, then you were probably told about the royal, queen's gambit, the defense of Philidor, or the King's Indian defense. All these debuts are applied at the beginning of the game. The thing is that they have long been and deep enough (up to 20 moves) calculated. Endgames in chess are also very well calculated. One has only to search the Internet for requests: “endgame rook versus light piece”, “endgame two rooks versus queen”, etc., to be convinced of this. It turns out that it is necessary to calculate only the middle of the batch, and there, as stated above, heuristics are very effective.
In the mid-1990s, programs were created that could defeat a world champion. A vivid example is the Deep Blue - Kasparov match. If in 1996 Kasparov lost only one game, but won the match, then in 1997 Deep Blue won Kasparov not in a separate game, but throughout the match.
The main difference between shogi and chess is that the pieces taken do not leave the game, but can return to any cell of the field at any time. This feature, together with the large size of the field and a large set of figures, make the shogi an incredibly difficult game. The number of parties increases dramatically to the number 10 226 , the exchange heuristics (the most common) becomes completely ineffective, as exchanges only complicate the game, the base of parties for shogi is also almost impossible to build, given their number.
The overwhelming majority of programs use the minimax strategy described above and the main difference in the programs is an algorithm for evaluating position and heuristics. Now matches between programs and professionals are forbidden, so as not to detract from the dignity of professional players, but from time to time the association shogi gives permission for the matches. The greatest achievement of AI in this game is the victory over the strongest of women. Ichiyo Shimizu played against the Akara program. Strictly speaking, Akara is not one program, but 4 independent engines. The decision on a better course is made by simple voting. Despite significant progress in the field of AI in shogi, programs are not yet able to outperform the strongest player.
More interesting is the situation in the game of go. The number of final positions in go is 10,171 ; this excludes direct enumeration of all options.
Unfortunately, the minimax search tree also works very poorly. The fact is that in the number of possible positions it grows very quickly and even supercomputers cannot sort out moves with sufficient speed. The best programs are able to “look into the future” for 12 turns. The resulting positions are evaluated and the best options are selected. For these options, the program begins to analyze the game again, trying to choose the best option. And so several times. One of the features of Go is that in this game, strategic thinking is much more important than tactical. And even if the program achieves a local tactical advantage, the real master still wins.
Nevertheless, programmers have found a very original algorithm that allows programs to play at the professional level (victory over the strongest players, as in the shootings, is out of the question).
The basic idea is to use the search algorithm in the Monte Carlo tree. From the title it is clear that this is a randomized algorithm. How is it used in go? The program randomly selects several million games that can be played from the current position. Moreover, each game is played to the end, the program calculates the profitability of the move, the only restriction is following the rules.
After losing millions of games to the end, the program receives some statistics about the probability of winning after the first move. According to these statistics, the program decides that such a move will lead to a gain with a probability of 5%, such and such - 3%, and so on. Then the program simply selects the move with the highest probability of winning and repeats the algorithm. As a result, the program makes a move that most likely leads to victory.
Using this method allowed the program to win against the strongest player, albeit with a handicap of 7 stones.
Is it possible that sooner or later the moment will come when programs will start winning people in 100% of games? Of course not, we always have a bottle!
Below is a short story about computer algorithms used in intellectual games.

We begin the consideration of algorithms with one of the most simple games: with daggers and crosses. I'm sure almost all of you can play in such a way that you never lose, but let's see how a computer does it.
Almost all games can be represented as a so-called. decision trees, where each node will represent one step of solving the problem (a move in the game), a branch in the tree corresponds to a solution that leads to a more complete solution, the sheets represent the final solution (final positions). Our goal is to find in the tree the best way from root to leaf.
Decision trees are usually incredibly large. For the tic-tac-toe game we are considering, the tree contains more than half a million knots. It is clear that in checkers, chess, and especially segah and go, trees are much more.
But, nevertheless, using the example of a children's game, one can consider methods that allow one to find optimal solutions in very large trees.
If a player has n possible moves, then the corresponding node will have n branches (descendants). For example, in noughts and crosses, the root node corresponds to an empty field. The first player can put a cross on any of the 9 squares. Each possible move will correspond to a branch originating from the root node. When a player has put a cross, the second player can place a zero in any of the remaining eight squares. Each of these moves corresponds to a branch originating from the node representing the current position of the cross on the board. The figure shows a small fragment of the tree under study.

As you can see from the picture, the game tree is growing extremely fast. If the tree continues to grow in this way, then the whole tree will contain 9! = 362880 leaves.
In fact, many possible nodes in the game tree are prohibited by the rules. For example, if one of the players has already won, then the tree can be completed at this stage. Removing all impossible nodes will reduce the tree to a quarter of a million sheets. But it is still a very, very large tree and it will take an inadmissibly long time to complete it. For more complex games, trees are simply unimaginable size. If in chess at each step the player would have 16 possible moves, there would be more than a trillion nodes in the tree after five moves.
To perform a search in the game tree, you need to be able to determine the value of the position of the playing field. In the tic-tac-toe for the first player, the positions in which the three crosses are arranged in a row are important, since the first player wins. The value of the player who puts a zero in these positions is very small, because at the same time he loses.
Each player can be assigned four values for a specific position on the field:
• 4 - winning;
• 3 - not clear situation;
• 2 - draw;
• 1 - loss;
For an exhaustive study of the game tree, you can use the minimax strategy. In doing so, we will try to minimize the maximum value that a position can have for an opponent after the next move. First, the maximum value that the opponent can dial after each of your possible moves is determined. Then the turn is chosen, at which the opponent gets the minimum value.
The procedure of finding the optimal course calculates the value of the field position. This procedure explores every possible move. For each move, she recursively calls herself to determine the value that the position of the opponent will have. Then she chooses a move that gives the opponent a minimum value. The recursive treatment of the procedure to yourself will continue until one of the three possible events occurs. First, the position in which the player wins can be found. In this case, the procedure sets the field position value to 4. In case the player loses, the field value will be set to 1. Secondly, a position in which no player can make a move can be found. The game ends in a draw, so the procedure sets the position to 2. And finally, the procedure can achieve a predetermined recursion depth. If it exceeds the allowable depth, then the field value is set to 3, indicating an indefinite outcome. The maximum recursion depth prevents the program from spending too much time. This is especially important for complex games, like chess, where the search can last for almost infinitely long time. The maximum recursion depth also allows you to set the skill level. The deeper a program can explore a tree, the better its moves will be.
The picture shows the game tree at the end of the game. The first and third moves lead to the victory of the player playing with zeros, so these moves have the value 4 for him. The second possible move leads to a draw and has the value 2. The program chooses the second move, because it gives the player the zeroes the smallest field value.

')
If the minimax algorithm would be the only tool for the study of game trees, then the search of large trees would be quite difficult. Fortunately, there are several techniques that you can use to search in large trees.
First, you can remember the first few moves chosen by the game experts. If you select the first move for the program, the search tree will be reduced by 9 times. In fact, the program should not go through the tree until the opponent has made a move. In this case, both the computer and his opponent have already chosen branches, therefore the tree will contain only 7! = 5040 branches.
Using additional memory to store multiple moves significantly reduces the time required to search the tree.
Another way to improve the search is to specify important patterns. In chess, such patterns can be positions that threaten several pieces at once, the king or the queen. In case the chess program notices the exchange pattern, it can temporarily change the depth of the recursion to view the series of exchanges to the end and decide whether the exchange will be beneficial. If the exchange does occur, the number of the remaining figures becomes smaller and the search in the tree is simplified.
And, finally, in more complex cases it is necessary to use heuristics. For example, in chess, the usual heuristic is gain advantage. When your opponent has fewer strong pieces and the same number of weak pieces with you, you should go for an exchange whenever possible.
How are things in reality (checkers and chess)
Even a schoolboy can completely bust a tree in noughts and crosses. In checkers, the number of possible positions is estimated to be 10 20 . This is very, very much, but in 2007 the supercomputer was able to calculate all possible moves. That is, since 2007, a person cannot (even theoretically) win over a computer.
With chess, brute force is hardly possible in the near future. The number of all possible positions in chess is estimated by the number 10 46 . This number is so large that even a supercomputer will need astronomical time to sort through these positions. Nevertheless, in chess there is a certain progress. It’s impossible to go through all the positions, but heuristics and position bases are very effective. If you ever learned to play chess, then you were probably told about the royal, queen's gambit, the defense of Philidor, or the King's Indian defense. All these debuts are applied at the beginning of the game. The thing is that they have long been and deep enough (up to 20 moves) calculated. Endgames in chess are also very well calculated. One has only to search the Internet for requests: “endgame rook versus light piece”, “endgame two rooks versus queen”, etc., to be convinced of this. It turns out that it is necessary to calculate only the middle of the batch, and there, as stated above, heuristics are very effective.
In the mid-1990s, programs were created that could defeat a world champion. A vivid example is the Deep Blue - Kasparov match. If in 1996 Kasparov lost only one game, but won the match, then in 1997 Deep Blue won Kasparov not in a separate game, but throughout the match.
How are things going in reality (shogi and go)
The main difference between shogi and chess is that the pieces taken do not leave the game, but can return to any cell of the field at any time. This feature, together with the large size of the field and a large set of figures, make the shogi an incredibly difficult game. The number of parties increases dramatically to the number 10 226 , the exchange heuristics (the most common) becomes completely ineffective, as exchanges only complicate the game, the base of parties for shogi is also almost impossible to build, given their number.
The overwhelming majority of programs use the minimax strategy described above and the main difference in the programs is an algorithm for evaluating position and heuristics. Now matches between programs and professionals are forbidden, so as not to detract from the dignity of professional players, but from time to time the association shogi gives permission for the matches. The greatest achievement of AI in this game is the victory over the strongest of women. Ichiyo Shimizu played against the Akara program. Strictly speaking, Akara is not one program, but 4 independent engines. The decision on a better course is made by simple voting. Despite significant progress in the field of AI in shogi, programs are not yet able to outperform the strongest player.
More interesting is the situation in the game of go. The number of final positions in go is 10,171 ; this excludes direct enumeration of all options.
Unfortunately, the minimax search tree also works very poorly. The fact is that in the number of possible positions it grows very quickly and even supercomputers cannot sort out moves with sufficient speed. The best programs are able to “look into the future” for 12 turns. The resulting positions are evaluated and the best options are selected. For these options, the program begins to analyze the game again, trying to choose the best option. And so several times. One of the features of Go is that in this game, strategic thinking is much more important than tactical. And even if the program achieves a local tactical advantage, the real master still wins.
Nevertheless, programmers have found a very original algorithm that allows programs to play at the professional level (victory over the strongest players, as in the shootings, is out of the question).
The basic idea is to use the search algorithm in the Monte Carlo tree. From the title it is clear that this is a randomized algorithm. How is it used in go? The program randomly selects several million games that can be played from the current position. Moreover, each game is played to the end, the program calculates the profitability of the move, the only restriction is following the rules.
After losing millions of games to the end, the program receives some statistics about the probability of winning after the first move. According to these statistics, the program decides that such a move will lead to a gain with a probability of 5%, such and such - 3%, and so on. Then the program simply selects the move with the highest probability of winning and repeats the algorithm. As a result, the program makes a move that most likely leads to victory.
Using this method allowed the program to win against the strongest player, albeit with a handicap of 7 stones.
Is it possible that sooner or later the moment will come when programs will start winning people in 100% of games? Of course not, we always have a bottle!
Source: https://habr.com/ru/post/143552/
All Articles