Accurate determination of the region by GPS coordinates
When developing one application, there was a problem of access control for regions.
The problem of determining whether an object belongs to any region of Russia by its GPS coordinates has arisen
The first thing we started using was the Google API,
after they registered aliases for the returned rows and payment for access (to remove the limit on requests), everything worked.
And everything was fine until Google changed the issue, for example, it was before: Moskovskaya oblast ', it became Moscow oblast'
Here it was decided not to rely on Google, but to define the region on its own.
')
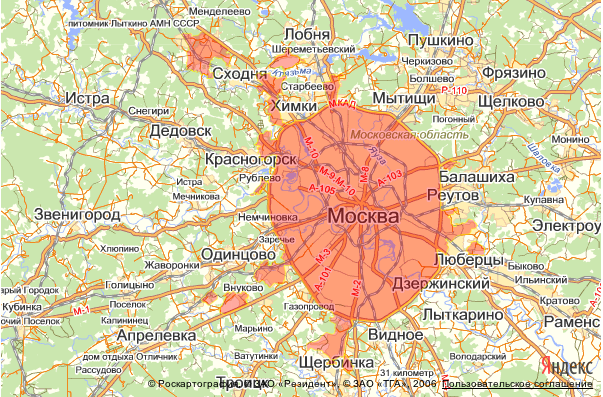
The first thing that came to mind was: parse the returned Yandex data (in Yandex maps of version 1.x there was a module for working with regions)
So did, it turned out 2 tables.
The names of the regions were stored in one, in the second coordinates of the polygon, describing the region. (83 - regions and 8500 - points)
An algorithm was found to check whether a point lies in a polygon. The code was rewritten from C to PHP, it makes no sense to understand how it works, it just works.
$ sx, $ sy - coordinates of the point that we check
$ coords - coordinates of points of a convex polygon (sorted in traversal order):
$ coords = array (
array ('x' => 66.6634, 'y' => '66 .4433 '),
etc.
)
$ x, $ y - the names of the keys in the array
Call example:
Returns true if the point lies inside the polygon.
Now, just by looking at the areas for a point, we get the answer.
Everything would be fine, but 8500 points of the regional boundaries for Russia are very few. The spread will turn out + - 50 km
To get more accuracy - we need more points of regional borders.
Searching in the open spaces a resource was found that freely gives us these points: gis-lab.info/qa/rusbounds-rosreestr.html (thanks to the enthusiasts for your work)
For some reason, I chose the KML format (probably because I knew how to open it - this is the format that Google Earth supports)
I parsed the data and now the tables turned out to be fatter. The table with the coordinates of the points of the regional boundaries has become 620,000 points (34 mb)
Now, if we check by the old algorithm that a point belongs to a region polygon - on an old Core 2 Duo - about 70 seconds.
Not an option. The algorithm needs to be optimized:
For example, Moscow:
We have 2,064 points of the polygon (in fact, several polygons):

But now it is enough for us to determine only the possibility that the point will be in this area. Therefore, we use the algorithm for traversing points and constructing a convex polygon.
algolist.manual.ru
Here is its implementation in PHP:
At the output we get an array of points of a convex polygon.
For Moscow; 19 points:
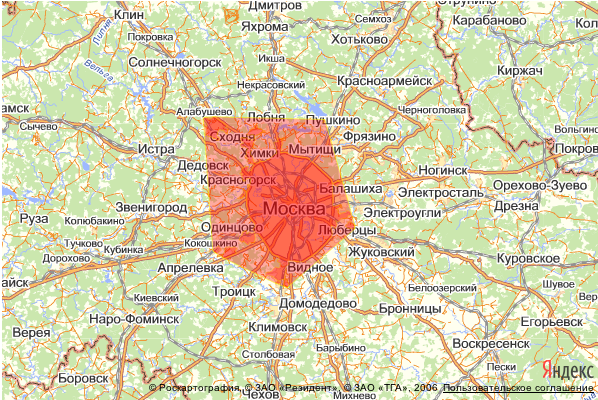
In the figure, the first layer marked all 2500 points of Moscow + layer, which we obtained after calculating a convex polygon.
For each region we will generate such a region.
Now we will refine our algorithm and we will first check the possibility that the point may lie in the region — there may be several such regions.
Now, after running all the areas, we will run the areas in which it is possible that the point lies, using the algorithm described above.
Total: 0.177sec on a weak Core 2 Duo
In fact, there is another difficulty - these are enclaves (Moscow lies inside the Moscow region, like Peter, it was decided to use priorities, first it is checked whether the point in Moscow lies, and then in the Moscow region)
The problem of determining whether an object belongs to any region of Russia by its GPS coordinates has arisen
The first thing we started using was the Google API,
after they registered aliases for the returned rows and payment for access (to remove the limit on requests), everything worked.
And everything was fine until Google changed the issue, for example, it was before: Moskovskaya oblast ', it became Moscow oblast'
Here it was decided not to rely on Google, but to define the region on its own.
')

The first thing that came to mind was: parse the returned Yandex data (in Yandex maps of version 1.x there was a module for working with regions)
So did, it turned out 2 tables.
The names of the regions were stored in one, in the second coordinates of the polygon, describing the region. (83 - regions and 8500 - points)
An algorithm was found to check whether a point lies in a polygon. The code was rewritten from C to PHP, it makes no sense to understand how it works, it just works.
$ sx, $ sy - coordinates of the point that we check
$ coords - coordinates of points of a convex polygon (sorted in traversal order):
$ coords = array (
array ('x' => 66.6634, 'y' => '66 .4433 '),
etc.
)
$ x, $ y - the names of the keys in the array
public static function into_poly($sx, $sy, &$coords, $x='x', $y='y') { Profiler::start('Detect collision', __FUNCTION__); $pj=0; $pk=0; $wrkx=0; $yu = 0; $yl = 0; $n = count($coords); for ($pj=0; $pj<$n; $pj++) { $yu = $coords[$pj][$y]>$coords[($pj+1)%$n][$y]?$coords[$pj][$y]:$coords[($pj+1)%$n][$y]; $yl = $coords[$pj][$y]<$coords[($pj+1)%$n][$y]?$coords[$pj][$y]:$coords[($pj+1)%$n][$y]; if ($coords[($pj+1)%$n][$y] - $coords[$pj][$y]) $wrkx = $coords[$pj][$x] + ($coords[($pj+1)%$n][$x] - $coords[$pj][$x])*($sy - $coords[$pj][$y])/($coords[($pj+1)%$n][$y] - $coords[$pj][$y]); else $wrkx = $coords[$pj][$x]; if ($yu >= $sy) if ($yl < $sy) { if ($sx > $wrkx) $pk++; if (abs($sx - $wrkx) < 0.00001) return 1; } if ((abs($sy - $yl) < 0.00001) && (abs($yu - $yl) < 0.00001) && (abs(abs($wrkx - $coords[$pj][$x]) + abs($wrkx - $coords[($pj+1)%$n][$x]) - abs($coords[$pj][$x] - $coords[($pj+1)%$n][$x])) < 0.0001)) return 1; } if ($pk%2) return 1; else return 0; } Call example:
$coords = array(
array('lng'=> 66.6634, 'lat' => '66.4433'),
array('lng'=> 66.6534, 'lat' => '66.4433'),
array('lng'=> 66.6434, 'lat' => '66.4433'),
array('lng'=> 66.6334, 'lat' => '66.4433'),
);
$in = into_poly(66.4455, 66.2255, &$coords, $x='lng', $y='lat');
Returns true if the point lies inside the polygon.
Now, just by looking at the areas for a point, we get the answer.
Everything would be fine, but 8500 points of the regional boundaries for Russia are very few. The spread will turn out + - 50 km
To get more accuracy - we need more points of regional borders.
Searching in the open spaces a resource was found that freely gives us these points: gis-lab.info/qa/rusbounds-rosreestr.html (thanks to the enthusiasts for your work)
For some reason, I chose the KML format (probably because I knew how to open it - this is the format that Google Earth supports)
I parsed the data and now the tables turned out to be fatter. The table with the coordinates of the points of the regional boundaries has become 620,000 points (34 mb)
Now, if we check by the old algorithm that a point belongs to a region polygon - on an old Core 2 Duo - about 70 seconds.
Not an option. The algorithm needs to be optimized:
For example, Moscow:
We have 2,064 points of the polygon (in fact, several polygons):

But now it is enough for us to determine only the possibility that the point will be in this area. Therefore, we use the algorithm for traversing points and constructing a convex polygon.
algolist.manual.ru
Here is its implementation in PHP:
public static function sort_points($mass, $x = 'x', $y = 'y'){ $current=0; $next=0; $p1 = $mass[0]; $mass2 = array(); // for ($i=1; $i<count($mass); $i++){ if ( ($p1[$y] > $mass[$i][$y]) || ($p1[$y] == $mass[$i][$y] && $p1[$x] < $mass[$i][$x]) ) { $p1 = $mass[$i]; $current = $i; } } $n = count($mass); $p0 = $p1; $p0[$x]--; $mass2[] = $mass[$current]; $first = $current; // do{ $cmax_not_set=1; for ( $i=0; $i<$n; $i++ ) { $key = $i; // if ( $mass[$current][$x] == $mass[$key][$x] && $mass[$current][$y] == $mass[$key][$y] ) continue; // 1 if ($cmax_not_set) { $next = $key; $cmax_not_set=0; continue; } $v1_x = $mass[$key][$x] - $mass[$current][$x]; $v1_y = $mass[$key][$y] - $mass[$current][$y]; $v2_x = $mass[$next][$x] - $mass[$current][$x]; $v2_y = $mass[$next][$y] - $mass[$current][$y]; // $c = $v1_x * $v2_y - $v1_y * $v2_x; if ( $c > 0 ) $next = $key; // if ( ($c==0) && ( self::_dist($mass[$current], $mass[$key], $x, $y) > self::_dist($mass[$current], $mass[$next], $x, $y) ) ) $next = $key; } // $mass2[] = $mass[$next]; $current = $next; }while($first != $next); return $mass2; } At the output we get an array of points of a convex polygon.
For Moscow; 19 points:

In the figure, the first layer marked all 2500 points of Moscow + layer, which we obtained after calculating a convex polygon.
For each region we will generate such a region.
Now we will refine our algorithm and we will first check the possibility that the point may lie in the region — there may be several such regions.
Now, after running all the areas, we will run the areas in which it is possible that the point lies, using the algorithm described above.
Total: 0.177sec on a weak Core 2 Duo
In fact, there is another difficulty - these are enclaves (Moscow lies inside the Moscow region, like Peter, it was decided to use priorities, first it is checked whether the point in Moscow lies, and then in the Moscow region)
Source: https://habr.com/ru/post/143277/
All Articles