How to properly sort content based on user ratings

In the original, the name sounds like “How Not To Sort By Average Rating”. I thought that the literal translation “How not to sort by average rating” would be poorly understood and reflects the content of the article worse.

Formulation of the problem

You do web programming. You have users who rate content on your site. You want to place highly valued content at the top, and low rated content at the bottom. To do this, based on user ratings, you need to calculate a certain “rating”.
')

Wrong decision number 1

= (  ) - (  )

Why is this wrong? Suppose one object has 600 positive ratings and 400 negative, i.e. in the end, 60% positive. Suppose further that the other object has 5500 positive ratings and 4500 negative, i.e. as a result, 55% positive. This algorithm will place the second object (with a rating of 1000, but with only 55% of positive ratings) above the first object (with a rating of 200 and with 60% of positive ratings). Wrong .

Sites that make such a mistake : Urban Dictionary

Wrong decision number 2

  =   = (  ) / (  )

Why is this wrong? Average rating works well if you always have a bunch of ratings. But suppose that one object has 2 positive ratings and 0 negative. Suppose further that the second object has 100 positive ratings and 1 negative. This algorithm will place the second object (with a bunch of positive ratings) below the first object (with a very small number of positive ratings). This is wrong .

Sites that make the same mistake : Amazon

Correct solution

  =      (Wilson)

Why is this correct? We need to find a balance between the proportion of positive assessments and the uncertainty of a small number of observations. Fortunately, the mathematical apparatus for solving this problem was developed in 1927 by Edwin Wilson. We want to know the following: “Having a set of data for me of assessments, is it possible with 95% probability to say what the“ real ”share of positive evaluations will be? Wilson gives the answer. Considering only positive and negative marks (i.e., not taking into account the 5-point rating system), the lower bound of the share of positive marks is calculated using the following formula:

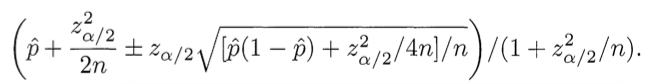
Use minus where plus / minus is written to calculate the lower bound. Here p̂ is the share of positive estimates, z _{α / 2} is the quantile ^* (1-α / 2) of the standard normal distribution, and n is the total number of estimates. Similar formula applied to Ruby:

^* Quantile in mathematical statistics - a value that a given random variable does not exceed with a fixed probability. Wikipedia

 require 'statistics2' def ci_lower_bound(pos, n, confidence) if n == 0 return 0 end z = Statistics2.pnormaldist(1-(1-confidence)/2) phat = 1.0*pos/n (phat + z*z/(2*n) - z * Math.sqrt((phat*(1-phat)+z*z/(4*n))/n))/(1+z*z/n) end

Here pos is the number of positive ratings, n is the total number of ratings, and confidence sets a statistically reliable level: set it to 0.95 so that you can count on the correctness of the lower bound, 95% probability, to 0.975 in order to have 97.5% probability. The number z in this function never changes. If you do not have convenient software for working with statistical data, or performance is critical for you, you can always hard-write the value for z. (Use 1.96 for a confidence level of 0.95).

Below, as an illustration, we give an SQL query that does what we need. We assume that we have a table of objects with positive and negative ratings for them, and we want to sort them by the lower limit of the 95% confidence interval:

 SELECT widget_id, ((positive + 1.9208) / (positive + negative) - 1.96 * SQRT((positive * negative) / (positive + negative) + 0.9604) / (positive + negative)) / (1 + 3.8416 / (positive + negative)) AS ci_lower_bound FROM widgets WHERE positive + negative > 0 ORDER BY ci_lower_bound DESC;

If someone does not believe that such a complex SQL query is able to return a useful result, simply compare this result with the results of the other two methods discussed above:

 SELECT widget_id, (positive - negative) AS net_positive_ratings FROM widgets ORDER BY net_positive_ratings DESC;

 SELECT widget_id, positive / (positive + negative) AS average_rating FROM widgets ORDER BY average_rating DESC;

You quickly make sure that quite a bit of extra math will make good content pop up. However, before running this SQL query on a large database, talk with your friendly administrator about the correct indexing of the tables. I originally developed this method for a Chuck Norris fact generator in honor of one of my teachers, but then I tried this method in places like Reddit , Yelp , and Digg .

Other uses of the method

Wilson's confidence interval is applicable not only for sorts. It can be used wherever you want to know with certainty what the proportion of people doing a certain act is . For example, it can be used for the following purposes:

Identify spam or abuse. How many people who saw the message will mark it as spam?
Create a list of the "best". How many people who saw the message will mark it as “the best”?
Create a list of the "most shared". How many people who saw the message will click on the share button?

This method can be much more useful for forming lists of the “best” in relation to the number of views, the number of downloads, or the number of purchases, rather than a conclusion on the number of positive ratings in relation to the total number of ratings. Many people discovering something mediocre will not bother to vote at all. By itself, the fact of viewing or buying something without a subsequent vote contains useful information about the quality of the object.

Ps from me

I did not translate the translation myself. All thanks karaboz .
I'm not completely sure about the accuracy of the translation of mathematical terms, I will be grateful for the clarification !

Initially, a discussion of the original article originated Facebook. There in the comments there are interesting things that I did not embed in so overloaded article.

Bookmarklets

In order to better see once than read 10 times on Habré, I made a couple of bookmarklets sorting out comments using the described method for Habr and the blog on Gift ~ 95% with 95% accuracy. I did it quickly, I checked it only in Chrome / Safari:

 javascript:jQuery.getScript('http://dl.dropbox.com/u/285016/code/habr_comment_by_rating.js');

 javascript:jQuery.getScript('http://dl.dropbox.com/u/285016/code/dd_comment_by_rating.js');

It looks like this (clickable):

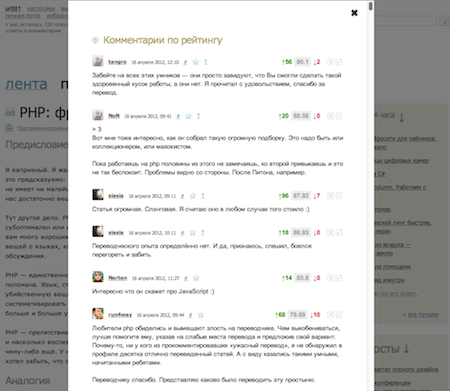
JavaScript rating implementation

In the functions below, the mined-in objects that do not receive a single positive vote are additionally processed. In this case, returns the-number_minus. In other cases, the rating will be in the range [0; 1). The number of positive and negative votes is passed as parameters.

 function wilson_score(up, down) { if (!up) return -down; var n = up + down; var z = 1.64485; //1.0 = 85%, 1.6 = 95% var phat = up / n; return (phat+z*z/(2*n)-z*Math.sqrt((phat*(1-phat)+z*z/(4*n))/n))/(1+z*z/n); }

Pps

Adapted the formula for an arbitrary scale of votes. Python code:

 def wilson_score(sum_rating, n, votes_range = [0, 1]): z = 1.64485 v_min = min(votes_range) v_width = float(max(votes_range) - v_min) phat = (sum_rating - n * v_min) / v_width / float(n) rating = (phat+z*z/(2*n)-z*sqrt((phat*(1-phat)+z*z/(4*n))/n))/(1+z*z/n) return rating * v_width + v_min

Here sum_rating is the sum of all votes, n is the number, votes_range is the range of possible ratings. The return value is in the specified votes_range range.

Source: https://habr.com/ru/post/143188/

All Articles