Image processing matrix filters
This article tells not only about the most common image processing filters, but also describes their operation algorithms in an understandable form. The article is focused primarily on programmers involved in image processing.
')
There are many filters using the convolution matrix; the main ones will be described below.
The convolution matrix is a matrix of coefficients that is “multiplied” by the pixel value of the image to obtain the desired result.
The following is the application of the convolution matrix:
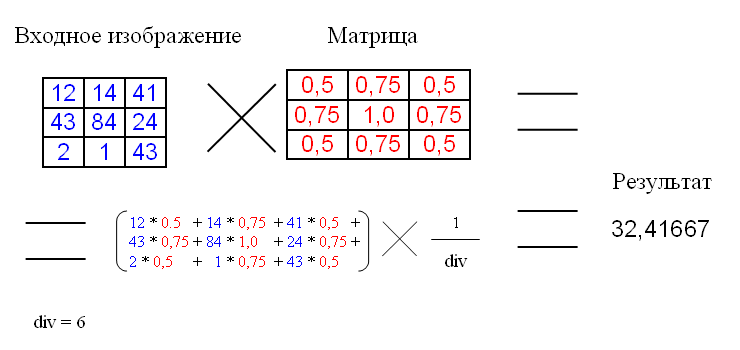
div is the coefficient of rationing so that the average intensity remains unchanged.
In the example, the matrix has a size of 3x3, although the size may be larger.
The most commonly used filter based on a convolution matrix is a blur filter.
Usually the matrix is filled in according to the normal (Gaussian law). Below is a 5x5 blur matrix filled out according to the Gaussian distribution law.
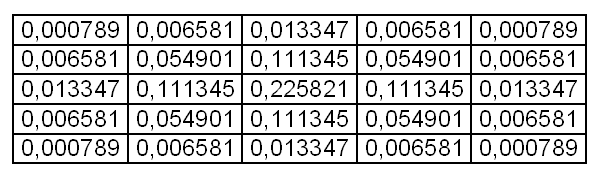
The coefficients are already normalized, so the div for this matrix is equal to one.
The strength of the blur depends on the size of the matrix.

It is worth mentioning the boundary conditions (this problem is relevant for all matrix filters). The upper left pixel does not have a “neighbor” to the right of it, therefore, we have nothing to multiply the coefficient of the matrix.
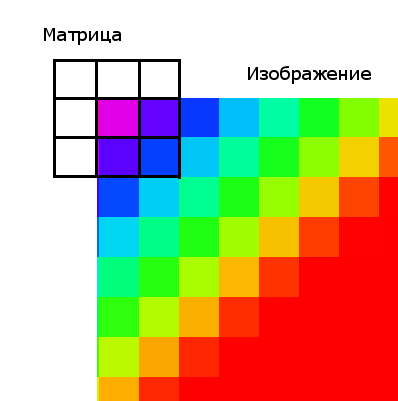
There are 2 solutions to this problem:
1. Apply a filter, only to the “window” of the image, which has the coordinates of the upper left corner [kernelSize / 2, kernelSize / 2], and for the lower right one [width - kernelSize / 2, height - kernelSize / 2]. kernelSize - the size of the matrix; width, height - the size of the image.
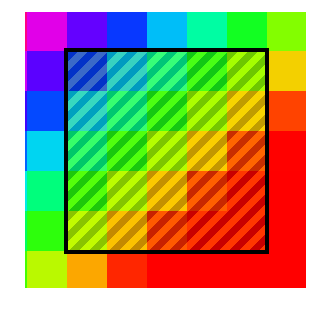
This is not the best way since the filter does not apply to the entire image. The quality of this is quite suffering if the filter size is large.
2. The second method (addition) requires the creation of an intermediate image. The idea is to create a temporary image with dimensions (width + 2 * kernelSize / 2, height + 2 * kernelSize / 2). The input image is copied to the center of the image, and the edges are filled with the extreme pixels of the image. Blur is applied to the intermediate buffer, and then the result is extracted from it.

This method has no deficiencies in quality, but it is necessary to perform extra calculations.
The Gaussian blur filter has complexity O (hi * wi * n * n), where hi, wi are the dimensions of the image, n is the size of the matrix (the core of the filter). This algorithm can be optimized with acceptable quality.
The square core (matrix) can be replaced by two one-dimensional: horizontal and vertical. For kernel size 5, they will be:

The filter is applied in 2 passes: first horizontal and then vertical (or vice versa) to the result.
The complexity of this algorithm will be O (hi * wi * n) + O (hi * wi * n) = 2 * O (hi * wi * n), which, for a kernel larger than two, is faster than the traditional square-matrix method.
To improve clarity, you must use the following matrix:
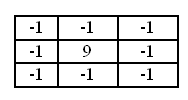
This matrix increases the difference in values at the boundaries. The div for this matrix is 1.

GIMP has a convolution matrix filter that simplifies the search for the matrix transformation you need.
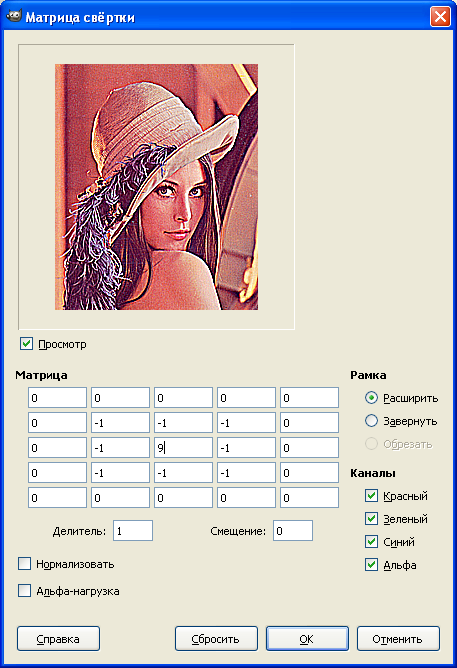
More information about filters based on the convolution matrix can be found in the article “Graphic Filters Based on a Twist Matrix” .
A median filter is usually used to reduce noise or “smooth” the image.

The filter works with matrices of different sizes, but unlike the convolution matrix, the matrix size only affects the number of pixels considered.
The median filter algorithm is as follows:
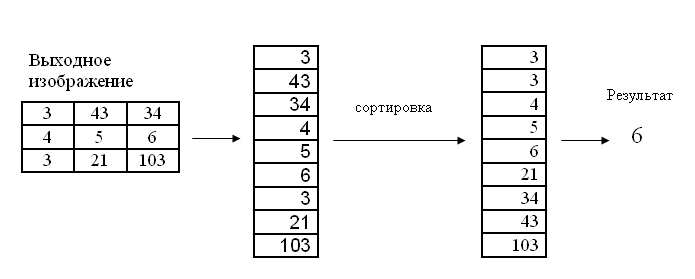
For the current pixel, the pixels that “fall” into the matrix are sorted, and the average value from the sorted array is selected. This value is the output for the current pixel.
Below is the work of the median filter for a kernel size of three.
Filters capacity and erosion are used to obtain morphological expansion or contraction, respectively. Simply put, for images, this means choosing a pixel with a maximum or minimum intensity from a neighborhood.

As a result of the increase, there is an increase in bright objects, and erosion - an increase in dark objects.
The filter uses an input image and a binary matrix. A binary matrix defines the shape of a neighborhood. Usually the neighborhood has a round shape.
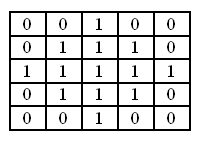
Filter capacity can be used to increase glare, bright reflections.
The article described some of the image processing filters, described their algorithms and application features.
ru.wikipedia.org/wiki/Median_filter
www.mathworks.com/help/toolbox/images/f18-12508.html#f18-20972
ru.wikipedia.org/wiki/Mathematical_morphology
habrahabr.ru/post/43895
Convolution matrix
')
There are many filters using the convolution matrix; the main ones will be described below.
The convolution matrix is a matrix of coefficients that is “multiplied” by the pixel value of the image to obtain the desired result.
The following is the application of the convolution matrix:

div is the coefficient of rationing so that the average intensity remains unchanged.
In the example, the matrix has a size of 3x3, although the size may be larger.
Blur filter
The most commonly used filter based on a convolution matrix is a blur filter.
Usually the matrix is filled in according to the normal (Gaussian law). Below is a 5x5 blur matrix filled out according to the Gaussian distribution law.

The coefficients are already normalized, so the div for this matrix is equal to one.
The strength of the blur depends on the size of the matrix.

It is worth mentioning the boundary conditions (this problem is relevant for all matrix filters). The upper left pixel does not have a “neighbor” to the right of it, therefore, we have nothing to multiply the coefficient of the matrix.

There are 2 solutions to this problem:
1. Apply a filter, only to the “window” of the image, which has the coordinates of the upper left corner [kernelSize / 2, kernelSize / 2], and for the lower right one [width - kernelSize / 2, height - kernelSize / 2]. kernelSize - the size of the matrix; width, height - the size of the image.

This is not the best way since the filter does not apply to the entire image. The quality of this is quite suffering if the filter size is large.
2. The second method (addition) requires the creation of an intermediate image. The idea is to create a temporary image with dimensions (width + 2 * kernelSize / 2, height + 2 * kernelSize / 2). The input image is copied to the center of the image, and the edges are filled with the extreme pixels of the image. Blur is applied to the intermediate buffer, and then the result is extracted from it.

This method has no deficiencies in quality, but it is necessary to perform extra calculations.
The Gaussian blur filter has complexity O (hi * wi * n * n), where hi, wi are the dimensions of the image, n is the size of the matrix (the core of the filter). This algorithm can be optimized with acceptable quality.
The square core (matrix) can be replaced by two one-dimensional: horizontal and vertical. For kernel size 5, they will be:

The filter is applied in 2 passes: first horizontal and then vertical (or vice versa) to the result.
The complexity of this algorithm will be O (hi * wi * n) + O (hi * wi * n) = 2 * O (hi * wi * n), which, for a kernel larger than two, is faster than the traditional square-matrix method.
Filter enhancement clarity
To improve clarity, you must use the following matrix:

This matrix increases the difference in values at the boundaries. The div for this matrix is 1.

GIMP has a convolution matrix filter that simplifies the search for the matrix transformation you need.

More information about filters based on the convolution matrix can be found in the article “Graphic Filters Based on a Twist Matrix” .
Median filter
A median filter is usually used to reduce noise or “smooth” the image.

The filter works with matrices of different sizes, but unlike the convolution matrix, the matrix size only affects the number of pixels considered.
The median filter algorithm is as follows:
For the current pixel, the pixels that “fall” into the matrix are sorted, and the average value from the sorted array is selected. This value is the output for the current pixel.
Below is the work of the median filter for a kernel size of three.

Erosion and build-up filters
Filters capacity and erosion are used to obtain morphological expansion or contraction, respectively. Simply put, for images, this means choosing a pixel with a maximum or minimum intensity from a neighborhood.

As a result of the increase, there is an increase in bright objects, and erosion - an increase in dark objects.
The filter uses an input image and a binary matrix. A binary matrix defines the shape of a neighborhood. Usually the neighborhood has a round shape.

Filter capacity can be used to increase glare, bright reflections.
Conclusion
The article described some of the image processing filters, described their algorithms and application features.
ru.wikipedia.org/wiki/Median_filter
www.mathworks.com/help/toolbox/images/f18-12508.html#f18-20972
ru.wikipedia.org/wiki/Mathematical_morphology
habrahabr.ru/post/43895
Source: https://habr.com/ru/post/142818/
All Articles