Persistent segment trees
Introduction
Data structures can be divided into two groups: ephemeral and persistent .
Data structures that store only their latest version are called ephemeral .
Persistent structures, that is, those that retain all their previous versions, can in turn be further divided into two subgroups: if the data structure allows only the latest version to be changed, it is called partially persistent , if it is allowed to change any version, such a structure is considered fully persistent .
Further, the segment tree and its fully persistent version will be considered.
All code is available on GitHub .
Segment tree
Those who are already familiar with segment trees can go directly to the section on the persistent version .
')
The segment tree is a data structure that allows for the given array
A quickly perform the following operations:Change(i, x)- change the value ofA[i]to xF(i, j)- calculatef(A[i], A[i + 1], ..., A[j])
Both operations are performed in O (log n). The function
f often taken as the sum, minimum or maximum.Description
Let
n be the length of array A , we will fill it with neutral elements until its length equals to a power of two (for example, if f is a sum, the array will be complemented with zeros).Now we will build such a binary tree that its leaves will be all elements of
A and the depth of all leaves is the same, and in all other vertices the values of f will be stored from the values of the child vertices.Consider as an example a tree of segments for the array
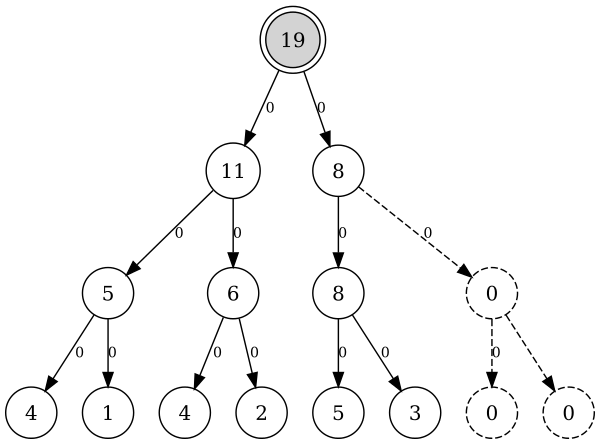
A = [4, 1, 4, 2, 5, 3] :![Tree segments for the array [4, 1, 4, 2, 5, 3] [4, 1, 4, 2, 5, 3]](https://habrastorage.org/storage2/549/053/b2f/549053b2f992ca7dae0fd0f6013b51ed.png)
It is convenient to keep such a tree as a binary heap: in the form of an array of vertices recorded in a row from top to bottom from left to right:
19 11 8 5 6 8 0 4 1 4 2 5 3 0 0
In this case, for a vertex with index
i its ancestor will be a vertex ((i - 1) / 2) , and the left and right child vertices will have indices (2 * i + 1) and (2 * i + 2) respectively (assuming that the elements in the array are numbered from zero).Building
It is convenient to build a segment tree recursively from top to bottom: for each vertex, construct the left and right child vertices, then calculate the value of
f from their values, and for sheets, simply write the corresponding value of the array into the tree.
By building a tree in this way, each vertex will be visited once, and since the number of vertices in the tree is Θ (n), the complexity of the construction is also Θ (n).
Change
After the value of any element was changed, some of the values of the ancestors of this element could deteriorate in the tree. This can be corrected by recalculating the values of the ancestors of this element, climbing up the tree.
For example, if in the array
A to replace A[3] by 10 , then the vertices with values 6 , 11 and 19 will be recalculated.Since the height of the tree is log n, the change operation will affect exactly log n vertices, which means that the asymptotic behavior of the operation O (log n).
Calculate F
This operation will be performed recursively from top to bottom.
Suppose that at an arbitrary vertex
v calculated F for the range l..r , then it is easy to check that the value of F for l..((l + r) / 2) counted in the left child vertex and for ((l + r) / 2 + 1)..r .Suppose that the query
F(i, j) received, and the current vertex is v . Two cases are possible:- Node
vhas already calculated the value ofF(i, j). Then the answer to the received request will be the value of the vertexv. - Node
vwrittenFfor a larger range. In this case, we recursively call the calculationF(i, (l + r) / 2)for the left child vertex andF((l + r) / 2 + 1, j)for the right, and the answer is f from these two values.
Example
Implementing a segment tree in C ++ .
Persistent Segment Tree
The persistence can be achieved in different ways, the easiest of them is to make a complete copy of the old version with each change and change it like a regular segment tree, but this method is too memory intensive and worsens the asymptotic behavior of the
Change operation to O (n).Building
Building a persistent tree of segments will be similar to building a regular tree of segments, except that now for each vertex you also have to explicitly store references to child vertices.
You will also need to store an array of vertices that are rooted in the corresponding versions of the tree. When constructing, a single vertex is added to it, which is the root of the resulting tree.
Since the only change compared to the ephemeral tree of segments is the addition of information about the left and right daughter vertices, the construction complexity remains the same, that is, Θ (n).
Change
Instead of completely copying the tree, if you change the vertices, only those vertices that should have been changed will be added to it, and instead of changing the values of the old vertices, the recalculated values will be saved to the new ones. All new vertices will refer to one vertex from the tree of the old version and one of the newly added ones.
Adding a new branch is done in the same way as building an entire tree, except that instead of building two child vertices, a new vertex is built only in the direction in which the modified vertex lies.
After that, the array of root vertices is updated.
![Persistent segment tree, version 1 (A [3] = 10) , 1 (A[3] = 10)](https://habrastorage.org/storage2/0c8/68b/0aa/0c868b0aa3d58afe2ef715d1b0f6c18e.png)
Since the change only adds log n vertices, the asymptotics of the operation is O (log n).
Calculate F
The calculation of F is done in the same way as an ephemeral tree. The only differences are: transitions to child nodes and starting from different root nodes.
Hence the complexity of O (log n).
Example
Implementing a persistent segment tree in C ++ .
Tasks
With the help of a persistent segment tree, you can solve the " Rollback " task ( parse the problem ). Solving the problem using the above implementation of the persistent segment tree is available on GitHub .
Also here you can read a discussion of the problem of the k-th order statistics on a range.
Source: https://habr.com/ru/post/142572/
All Articles