Compression without loss of information. Part two
First part.
In the second part, arithmetic coding and the Burrows-Wheeler transformation will be considered (the latter is often undeservedly forgotten in many articles). I will not consider the LZ family of algorithms, since there were already quite good articles about them in Habré.
So, let's start with arithmetic coding - in my opinion, one of the most elegant (in terms of the idea) compression methods.
')
In the first part, we looked at Huffman coding. Despite the fact that this is an excellent, time-tested algorithm, it (like any others) is not without its drawbacks. We illustrate the weak point of the Huffman algorithm with an example. When coding by the Huffman method, the relative frequency of the appearance of characters in the stream approaches frequencies that are multiple of a power of two. By the Shannon theorem, let me remind you, the best compression will be achieved if each symbol with frequency f is encoded with -log 2 f bits. Let's build a small chart (I apologize in advance, since I am not strong in building beautiful charts).
As you can see, in cases where the relative frequencies are not powers of two, the algorithm clearly loses its effectiveness. It is easy to check on a simple example of a stream of two symbols a and b with frequencies 253/256 and 3/256, respectively. In this case, ideally we will need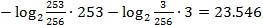
that is, 24 bits. At the same time, the Huffman method encodes these characters with codes 0 and 1, respectively, and the message will take 256 bits, which, of course, is less than 256 bytes of the original message (remember, we assume that initially each character is in byte size), but still 10 times less than optimum.
So, we proceed to the consideration of arithmetic coding, which will allow us to get the best result.
Like the Huffman method, arithmetic coding is an entropy compression method. Encoded data are presented in the form of a fraction, which is selected so that the text can be presented most compactly. What does this really mean?
Consider the construction of a fraction on the interval [0,1) (this interval is chosen for convenience of calculation), and for example, the input data in the form of the word "box". Our task will be to divide the initial interval into subintervals with lengths equal to the probabilities of the appearance of characters.
Create a probability table for our input text:
Here, "Frequency" means the number of occurrences of a character in the input stream.
We assume that these quantities are known both for encoding and decoding. When encoding the first character of the sequence (in our case, “ K orob”), the whole range from 0 to 1 is used. This range must be divided into segments according to the table.
The interval corresponding to the current encoded symbol is taken as the working interval. The length of this interval is proportional to the frequency of occurrence of the symbol in the stream.
After finding the interval for the current symbol, this interval is extended, and in turn is divided in accordance with the frequencies, as well as the previous ones (that is, for our example, in step 2 we must divide the interval from 0.4 to 0.6 into subintervals as how they did it in the first step). The process continues until the last character of the stream is encoded.
In other words, the i-th symbol will be assigned an interval
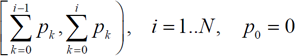
where N is the number of characters in the alphabet, p i is the probability of the i-th character.
In our case, it looks like this.
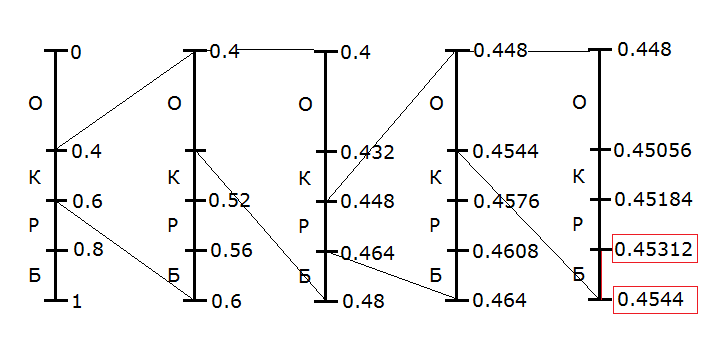
So, we have successively narrowed the interval for each character of the input stream, until we get the interval from 0.45312 to 0.4544 on the last character. That is what we will use when encoding.
Now we need to take any number lying in this interval. Let it be 0.454. Surprisingly (and for me, when I first studied this method, it was quite surprising), this number, in combination with the values ​​of the frequencies of the symbols, is enough to completely restore the original message.
However, for successful implementation, the fraction must be represented in binary form. Due to the feature of representing fractions in binary form (recall that some fractions having a finite number of digits in the decimal system have an infinite number of digits in binary), encoding is usually performed based on the upper and lower limits of the target range.
How does decoding happen? Decoding occurs in a similar way (not in the reverse order, but in a similar way).
We start with an interval from 0 to 1, broken down according to the frequencies of the characters. We check which interval our number falls into (0.454). The character corresponding to this interval will be the first character of the sequence. Next, we extend this interval to the full scale, and repeat the procedure.
For our case, the process will look like this:
Of course, nothing prevents us from continuing to reduce the interval and increase accuracy, getting more and more new "characters". Therefore, when encoding in this way, you need to either know in advance the number of characters of the original message, or limit the message to a unique character so that its end can be accurately determined.
When implementing the algorithm, some factors should be taken into account. Firstly, the algorithm in the form presented above can only encode short chains due to the limitation of bit depth. To avoid this limitation, real algorithms work with integers and operate with fractions, the numerator and denominator of which are an integer.
To estimate the degree of compression of arithmetic coding, we need to find the minimum number N, such that during the compression of the last character, we can certainly find a number in the binary representation of which, after N characters, only zeros go. For this, the length of the interval must be no less than 1/2 N. It is known that the length of the interval will be equal to the product of the probabilities of all symbols.
Consider the sequence of symbols a and b proposed at the beginning of the article with probabilities 253/256 and 3/256. The length of the last working interval for a chain of 256 characters will be equal to
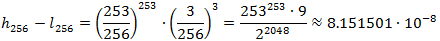
In this case, the required N will be equal to 24 (23 gives too large an interval, and 25 will not be minimal), that is, we will spend on coding only 24 bits, against 256 bits of the Huffman method.
So, we found out that compression methods show different efficiency on different data sets. Proceeding from this, a quite logical question arises: if compression algorithms work better on certain data, is it possible to perform some operations with data before compression to improve their “quality”?
Yes it is possible. For illustration, consider the Burrows-Wheeler transform, which turns a data block with complex dependencies into a block whose structure is easier to model. Naturally, this transformation is also completely reversible. The authors of the method are David Wheeler and Michael Burrows (according to the wiki, he now works at Google).
So, the Burrows-Wheeler algorithm (hereinafter, for brevity, I will call it BTW - Burrows-Wheeler Transform) transforms the input block into a form more convenient for compression. However, as practice shows, the usual methods obtained as a result of the block conversion are not as successful as they were specially designed for this, therefore, for practical use, the BWT algorithm cannot be considered separately from the corresponding data coding methods, but since our goal is to learn how it works, Nothing wrong with that.
In the original article, published in 1994, the authors proposed the implementation of coding on three algorithms:
True, the second step can be replaced by another similar algorithm, or completely eliminated due to the complexity of the coding phase. It is important to understand that BWT does not affect the size of the data , it only changes the location of the blocks.
BWT is a block algorithm, that is, it operates on data blocks, and knows in advance about the composition of block elements of a certain size. This makes it difficult to use BWT in cases where character-by-character compression or on-the-fly compression is necessary. In principle, such an implementation is possible, but the algorithm will turn out ... not very fast.
The principle of conversion is extremely simple. Consider it on the classic "book" example - the word "abracadabra", which perfectly suits us according to several criteria: there are many repeated symbols in it, and these symbols are distributed fairly evenly over the word.
The first step in the conversion will be to compile a list of cyclic permutations of the source data. In other words, we take the source data, and move the last character to the first place (or vice versa). We perform this operation until we get the original string again. All strings obtained in this way will be all cyclic permutations. In our case, it looks like this:
We will consider this as a matrix of characters, where each cell is one character, respectively, the string corresponds to the whole word. We mark the source row and sort the matrix.
Sorting is done first by the first character, then for those lines where the first character matches - by the second, and so on. After this sorting, our matrix will look like this:
In general, this transformation is almost complete: all that remains to be done is to write down the last column, while not forgetting to remember the number of the original row. By doing this, we get:
or differently
As you can see, the distribution of characters has become much better: now 4 out of 5 characters “a” stand side by side, like both symbols “b”.
As I already mentioned, the transformation is completely reversible. This is understandable, because otherwise there would be no point in it. So how to restore the original appearance of the message?
First we need to sort our characters in order. This will give us the string "aaaaabbdkrr." Since our cyclic permutation matrix was sorted in order, this sequence of letters is nothing but the first column of our cyclic permutation matrix. In addition, we know the last column (in fact, the result of the transformation itself). So, at this stage, we can restore the matrix to something like this:
Since the matrix was obtained by a cyclic shift, the symbols of the last and first columns form pairs. Sorting these pairs in ascending order, we will get the first two columns. Then, these two columns and the last form three characters already, and so on.
In the end, we completely restore the matrix, and since we know the number of the line containing the original data, we can easily get their original form.
In other words, the restoration is carried out as follows:
These two steps need to be repeated until the matrix is ​​completely filled.
For our example, the first four steps of recovery will look like this:
After we have proved the reversibility of the data, we will prove that in order to implement the algorithm, it is not necessary to store the entire matrix in memory. Indeed, if we completely stored a matrix corresponding to, for example, a block of 1 megabyte in size, then we would need a tremendous amount of memory - because the matrix is ​​square. Naturally, this option is invalid.
For the inverse transformation, in addition to the actual data, we need an inverse transformation vector - an array of numbers, the size of which is equal to the number of characters in the block. Thus, memory costs for linear conversion grow linearly with the size of the block.
During the inverse transformation, the same actions were performed to obtain the next column of the matrix. Namely, the new line was obtained by combining the character of the last column of the old line and the known characters of the same line. Of course, after sorting, the new row was moved to another position in the matrix. It is important that when adding any column, the movement of rows to the new position should be the same. To get the vector of the inverse transform, you need to determine the order of obtaining the characters of the first column from the characters of the last one, that is, sort the matrix by new row numbers
The transformation vector is formed from the values ​​of line numbers: {2,5,6,7,8,9,10,1,3,0,4}.
Now you can easily get the original string. Take an element of the vector of the inverse transform that corresponds to the number of the original row in the matrix: T [2] = 6. In other words, as the first character of the source line, you must take the sixth character of the string "rdacraaabb" - the symbol "a".
After that, we look at which symbol has moved the found symbol “a” to the second position among the same with it. To do this, we take the number from the transform vector of the string from which the character “a” was taken: this is number 6.
Then we look at the line having the number 6 and choose the last character from there - the symbol “b”. Continuing this procedure for the remaining characters, we will easily restore the original string.
Moving a stack of books is an intermediate algorithm that the authors recommend using after BWT and before direct coding. The algorithm works as follows.
Consider the string "rdakraaabb", obtained by us on BWT in the previous section. In this case, our alphabet consists of 5 characters. Ordering them, we get
M = {a, b, d, k, p}.
So, we use on our line an algorithm for moving a stack of books. The first character of the string ("p") is in the alphabet in 4th place. This number (4) we write to the output block. Then we put the newly used symbol in the first place, and repeat the process with the second symbol, then with the third, and so on. The processing will look like this (under the “number” I assume the number that will go to the output stream):
The result will be a sequence
At this stage, it is not entirely clear what is the use of this algorithm. In fact, there is a use. Consider a more abstract sequence:
For a start, just encode it using the Huffman method. For clarity, we assume that the costs of storing a tree using moving a stack of books, and without it, are the same.
The probabilities of the appearance of all four characters in our case are equal to ÂĽ, that is, the encoding of each character requires 2 bits. It is easy to calculate that the encoded string will take 40 bits.
Now let's change the string with the algorithm for moving a stack of books. At the beginning of the alphabet has the form
After using the algorithm, the string will be
In this case, the frequency of the appearance of characters will change greatly:
In this case, after encoding, we get a sequence of 15 + 6 + 3 + 3 = 27 bits, which is much less than 40 bits, which are obtained without moving a stack of books.
So, in this article, arithmetic coding was considered, as well as transformation algorithms, allowing to obtain a more “convenient” compression stream. It should be noted that the use of algorithms such as BWT is very dependent on the input stream. Efficiency is influenced by such factors as the lexigraphic sequence of characters, the directions of the bypass of the encoder (compression from left to right or right to left), block size, and so on. In the next part of the article I will consider some more complex algorithm used in real coders (which one I haven’t decided yet).
In the second part, arithmetic coding and the Burrows-Wheeler transformation will be considered (the latter is often undeservedly forgotten in many articles). I will not consider the LZ family of algorithms, since there were already quite good articles about them in Habré.
So, let's start with arithmetic coding - in my opinion, one of the most elegant (in terms of the idea) compression methods.
')
Introduction
In the first part, we looked at Huffman coding. Despite the fact that this is an excellent, time-tested algorithm, it (like any others) is not without its drawbacks. We illustrate the weak point of the Huffman algorithm with an example. When coding by the Huffman method, the relative frequency of the appearance of characters in the stream approaches frequencies that are multiple of a power of two. By the Shannon theorem, let me remind you, the best compression will be achieved if each symbol with frequency f is encoded with -log 2 f bits. Let's build a small chart (I apologize in advance, since I am not strong in building beautiful charts).
As you can see, in cases where the relative frequencies are not powers of two, the algorithm clearly loses its effectiveness. It is easy to check on a simple example of a stream of two symbols a and b with frequencies 253/256 and 3/256, respectively. In this case, ideally we will need
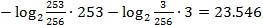that is, 24 bits. At the same time, the Huffman method encodes these characters with codes 0 and 1, respectively, and the message will take 256 bits, which, of course, is less than 256 bytes of the original message (remember, we assume that initially each character is in byte size), but still 10 times less than optimum.So, we proceed to the consideration of arithmetic coding, which will allow us to get the best result.
Arithmetic coding
Like the Huffman method, arithmetic coding is an entropy compression method. Encoded data are presented in the form of a fraction, which is selected so that the text can be presented most compactly. What does this really mean?
Consider the construction of a fraction on the interval [0,1) (this interval is chosen for convenience of calculation), and for example, the input data in the form of the word "box". Our task will be to divide the initial interval into subintervals with lengths equal to the probabilities of the appearance of characters.
Create a probability table for our input text:
| Symbol | Frequency | Probability | Range |
| ABOUT | 2 | 0.4 | [0.0, 0.4) |
| TO | one | 0.2 | [0.4, 0.6) |
| R | one | 0.2 | [0.6, 0.8) |
| B | one | 0.2 | [0.8, 1.0) |
Here, "Frequency" means the number of occurrences of a character in the input stream.
We assume that these quantities are known both for encoding and decoding. When encoding the first character of the sequence (in our case, “ K orob”), the whole range from 0 to 1 is used. This range must be divided into segments according to the table.
The interval corresponding to the current encoded symbol is taken as the working interval. The length of this interval is proportional to the frequency of occurrence of the symbol in the stream.
After finding the interval for the current symbol, this interval is extended, and in turn is divided in accordance with the frequencies, as well as the previous ones (that is, for our example, in step 2 we must divide the interval from 0.4 to 0.6 into subintervals as how they did it in the first step). The process continues until the last character of the stream is encoded.
In other words, the i-th symbol will be assigned an interval
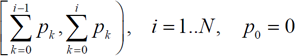
where N is the number of characters in the alphabet, p i is the probability of the i-th character.
In our case, it looks like this.
So, we have successively narrowed the interval for each character of the input stream, until we get the interval from 0.45312 to 0.4544 on the last character. That is what we will use when encoding.
Now we need to take any number lying in this interval. Let it be 0.454. Surprisingly (and for me, when I first studied this method, it was quite surprising), this number, in combination with the values ​​of the frequencies of the symbols, is enough to completely restore the original message.
However, for successful implementation, the fraction must be represented in binary form. Due to the feature of representing fractions in binary form (recall that some fractions having a finite number of digits in the decimal system have an infinite number of digits in binary), encoding is usually performed based on the upper and lower limits of the target range.
How does decoding happen? Decoding occurs in a similar way (not in the reverse order, but in a similar way).
We start with an interval from 0 to 1, broken down according to the frequencies of the characters. We check which interval our number falls into (0.454). The character corresponding to this interval will be the first character of the sequence. Next, we extend this interval to the full scale, and repeat the procedure.
For our case, the process will look like this:
Of course, nothing prevents us from continuing to reduce the interval and increase accuracy, getting more and more new "characters". Therefore, when encoding in this way, you need to either know in advance the number of characters of the original message, or limit the message to a unique character so that its end can be accurately determined.
When implementing the algorithm, some factors should be taken into account. Firstly, the algorithm in the form presented above can only encode short chains due to the limitation of bit depth. To avoid this limitation, real algorithms work with integers and operate with fractions, the numerator and denominator of which are an integer.
To estimate the degree of compression of arithmetic coding, we need to find the minimum number N, such that during the compression of the last character, we can certainly find a number in the binary representation of which, after N characters, only zeros go. For this, the length of the interval must be no less than 1/2 N. It is known that the length of the interval will be equal to the product of the probabilities of all symbols.
Consider the sequence of symbols a and b proposed at the beginning of the article with probabilities 253/256 and 3/256. The length of the last working interval for a chain of 256 characters will be equal to
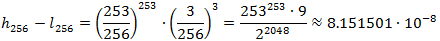
In this case, the required N will be equal to 24 (23 gives too large an interval, and 25 will not be minimal), that is, we will spend on coding only 24 bits, against 256 bits of the Huffman method.
Burrows - Wheeler Transformation
So, we found out that compression methods show different efficiency on different data sets. Proceeding from this, a quite logical question arises: if compression algorithms work better on certain data, is it possible to perform some operations with data before compression to improve their “quality”?
Yes it is possible. For illustration, consider the Burrows-Wheeler transform, which turns a data block with complex dependencies into a block whose structure is easier to model. Naturally, this transformation is also completely reversible. The authors of the method are David Wheeler and Michael Burrows (according to the wiki, he now works at Google).
So, the Burrows-Wheeler algorithm (hereinafter, for brevity, I will call it BTW - Burrows-Wheeler Transform) transforms the input block into a form more convenient for compression. However, as practice shows, the usual methods obtained as a result of the block conversion are not as successful as they were specially designed for this, therefore, for practical use, the BWT algorithm cannot be considered separately from the corresponding data coding methods, but since our goal is to learn how it works, Nothing wrong with that.
In the original article, published in 1994, the authors proposed the implementation of coding on three algorithms:
- Actually, BWT
- Transform Move-to-Front, known in Russian literature as moving a stack of books
- Statistical compression encoder obtained in the first two stages of data.
True, the second step can be replaced by another similar algorithm, or completely eliminated due to the complexity of the coding phase. It is important to understand that BWT does not affect the size of the data , it only changes the location of the blocks.
Transform algorithm
BWT is a block algorithm, that is, it operates on data blocks, and knows in advance about the composition of block elements of a certain size. This makes it difficult to use BWT in cases where character-by-character compression or on-the-fly compression is necessary. In principle, such an implementation is possible, but the algorithm will turn out ... not very fast.
The principle of conversion is extremely simple. Consider it on the classic "book" example - the word "abracadabra", which perfectly suits us according to several criteria: there are many repeated symbols in it, and these symbols are distributed fairly evenly over the word.
The first step in the conversion will be to compile a list of cyclic permutations of the source data. In other words, we take the source data, and move the last character to the first place (or vice versa). We perform this operation until we get the original string again. All strings obtained in this way will be all cyclic permutations. In our case, it looks like this:
We will consider this as a matrix of characters, where each cell is one character, respectively, the string corresponds to the whole word. We mark the source row and sort the matrix.
Sorting is done first by the first character, then for those lines where the first character matches - by the second, and so on. After this sorting, our matrix will look like this:
– In general, this transformation is almost complete: all that remains to be done is to write down the last column, while not forgetting to remember the number of the original row. By doing this, we get:
«>><<» or differently
«»,2 As you can see, the distribution of characters has become much better: now 4 out of 5 characters “a” stand side by side, like both symbols “b”.
Reversibility
As I already mentioned, the transformation is completely reversible. This is understandable, because otherwise there would be no point in it. So how to restore the original appearance of the message?
First we need to sort our characters in order. This will give us the string "aaaaabbdkrr." Since our cyclic permutation matrix was sorted in order, this sequence of letters is nothing but the first column of our cyclic permutation matrix. In addition, we know the last column (in fact, the result of the transformation itself). So, at this stage, we can restore the matrix to something like this:
| but | ... | R |
| but | ... | d |
| but | ... | but |
| but | ... | to |
| but | ... | R |
| b | ... | but |
| b | ... | but |
| d | ... | but |
| to | ... | but |
| R | ... | b |
| R | ... | b |
Since the matrix was obtained by a cyclic shift, the symbols of the last and first columns form pairs. Sorting these pairs in ascending order, we will get the first two columns. Then, these two columns and the last form three characters already, and so on.
In the end, we completely restore the matrix, and since we know the number of the line containing the original data, we can easily get their original form.
In other words, the restoration is carried out as follows:
- Attach the characters of the last column to the left to the characters of the first
- Sort all columns except last
These two steps need to be repeated until the matrix is ​​completely filled.
For our example, the first four steps of recovery will look like this:
-> -> -> ->... -> -> -> ->... -> -> -> ->... -> -> -> ->... -> -> -> ->... -> -> -> ->... -> -> -> ->... -> -> -> ->... -> -> -> ->... -> -> -> ->... -> -> -> ->... Resource costs when working
After we have proved the reversibility of the data, we will prove that in order to implement the algorithm, it is not necessary to store the entire matrix in memory. Indeed, if we completely stored a matrix corresponding to, for example, a block of 1 megabyte in size, then we would need a tremendous amount of memory - because the matrix is ​​square. Naturally, this option is invalid.
For the inverse transformation, in addition to the actual data, we need an inverse transformation vector - an array of numbers, the size of which is equal to the number of characters in the block. Thus, memory costs for linear conversion grow linearly with the size of the block.
During the inverse transformation, the same actions were performed to obtain the next column of the matrix. Namely, the new line was obtained by combining the character of the last column of the old line and the known characters of the same line. Of course, after sorting, the new row was moved to another position in the matrix. It is important that when adding any column, the movement of rows to the new position should be the same. To get the vector of the inverse transform, you need to determine the order of obtaining the characters of the first column from the characters of the last one, that is, sort the matrix by new row numbers
The transformation vector is formed from the values ​​of line numbers: {2,5,6,7,8,9,10,1,3,0,4}.
Now you can easily get the original string. Take an element of the vector of the inverse transform that corresponds to the number of the original row in the matrix: T [2] = 6. In other words, as the first character of the source line, you must take the sixth character of the string "rdacraaabb" - the symbol "a".
After that, we look at which symbol has moved the found symbol “a” to the second position among the same with it. To do this, we take the number from the transform vector of the string from which the character “a” was taken: this is number 6.
Then we look at the line having the number 6 and choose the last character from there - the symbol “b”. Continuing this procedure for the remaining characters, we will easily restore the original string.
Moving a stack of books
Moving a stack of books is an intermediate algorithm that the authors recommend using after BWT and before direct coding. The algorithm works as follows.
Consider the string "rdakraaabb", obtained by us on BWT in the previous section. In this case, our alphabet consists of 5 characters. Ordering them, we get
M = {a, b, d, k, p}.
So, we use on our line an algorithm for moving a stack of books. The first character of the string ("p") is in the alphabet in 4th place. This number (4) we write to the output block. Then we put the newly used symbol in the first place, and repeat the process with the second symbol, then with the third, and so on. The processing will look like this (under the “number” I assume the number that will go to the output stream):
| Symbol | Alphabet | room |
| R | abcdr | four |
| d | rabdk | 3 |
| but | drabk | 2 |
| to | adrbk | four |
| R | frame | 3 |
| but | rkadb | 2 |
| but | arcdb | 0 |
| but | arcdb | 0 |
| but | arcdb | 0 |
| b | arcdb | four |
| b | barcd | 0 |
The result will be a sequence
43243200040 At this stage, it is not entirely clear what is the use of this algorithm. In fact, there is a use. Consider a more abstract sequence:
For a start, just encode it using the Huffman method. For clarity, we assume that the costs of storing a tree using moving a stack of books, and without it, are the same.
The probabilities of the appearance of all four characters in our case are equal to ÂĽ, that is, the encoding of each character requires 2 bits. It is easy to calculate that the encoded string will take 40 bits.
Now let's change the string with the algorithm for moving a stack of books. At the beginning of the alphabet has the form
M={,,,}. After using the algorithm, the string will be
10002000030000300003 In this case, the frequency of the appearance of characters will change greatly:
| Symbol | Frequency | Probability | Huffman Code |
| 0 | 15 | 3/4 | 0 |
| 3 | 3 | 3/20 | ten |
| 2 | one | 1/20 | 110 |
| one | one | 1/20 | 111 |
In this case, after encoding, we get a sequence of 15 + 6 + 3 + 3 = 27 bits, which is much less than 40 bits, which are obtained without moving a stack of books.
Conclusion
So, in this article, arithmetic coding was considered, as well as transformation algorithms, allowing to obtain a more “convenient” compression stream. It should be noted that the use of algorithms such as BWT is very dependent on the input stream. Efficiency is influenced by such factors as the lexigraphic sequence of characters, the directions of the bypass of the encoder (compression from left to right or right to left), block size, and so on. In the next part of the article I will consider some more complex algorithm used in real coders (which one I haven’t decided yet).
Literature
- Vatolin D., Ratushnyak A., Smirnov M. Yukin V. Data Compression Methods. Device archivers, image and video compression; ISBN 5-86404-170-X; 2003
- Lidovsky V.V. Information Theory: Tutorial. - M .: Sputnik +, 2004.
- Semenyuk V.V. Economical coding of discrete information. - SPb .: SPbGITMO (TU), 2001.
- Witten IH, Neal RM, Cleary JG Arithmetic Coding for Data Compression, CACM, 1987.
Source: https://habr.com/ru/post/142492/
All Articles