Color coding

I have always been interested in the science of cryptography. At an early age, I loved magazines for children, in which the Russian alphabet was given, in which under each letter was its encrypted form, and after that it was necessary to guess a certain encrypted text using this alphabet. What a joy these puzzles brought me, I think many of you still remember them.

In this article I will not describe the known methods of encryption. Here we talk about color!
')
The basic encryption methods that I know are mainly using, so to speak, the character replacement algorithm. I admit honestly, before writing this article, I did not delve into cryptography and I know very little about it. So everything that will be written here is your own methods, suggestions and thoughts.

I believe that the color palette provides cryptography very large possibilities. Let us proceed to the consideration of various color encryption methods that came to my mind. Perhaps some of them already exist and are being applied, but I will repeat once again that I was a little googled ...

Let's start with the primitive. For a start, take just two colors, black and white. The Russian alphabet consists of 33 letters, so we draw a field consisting of 33 squares and divide it into 3 lines of 11 squares.



The sequence number of the letter in the alphabet will correspond to the number of the square in this figure, but this is not all. Let's try to write the phrase "Hi habr." Below are the alphabetical numbers of each letter of this phrase.

P - 17; R - 18; And - 10; IN 3; E - 6; T - 20; X - 23; A - 1; B - 2; R - 18.

Let's start painting over the squares that correspond to the numbers of the letters in black:
The letters P, P are shown below:



We have the letter I in turn, the sequence number of which is 10. But if we fill in the 10th cell of our table, it will lose its meaning, as we read the words starting from the first letter, and if the 10th cell is filled, then the first letter of our word will be I. Then Duplicate our table with 33 squares again and mark the letter in the new table already:



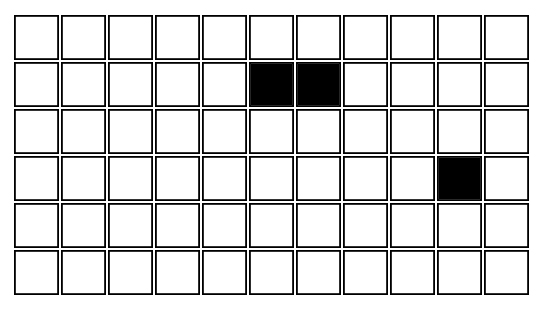
The letter B comes with the number - 3, which is less than 10, respectively, we need again a new table of 33 squares. I will not continue to describe each letter, and give the entire phrase in its entirety. In one table there is an encrypted phrase, in the second there is a sequence number and a letter.



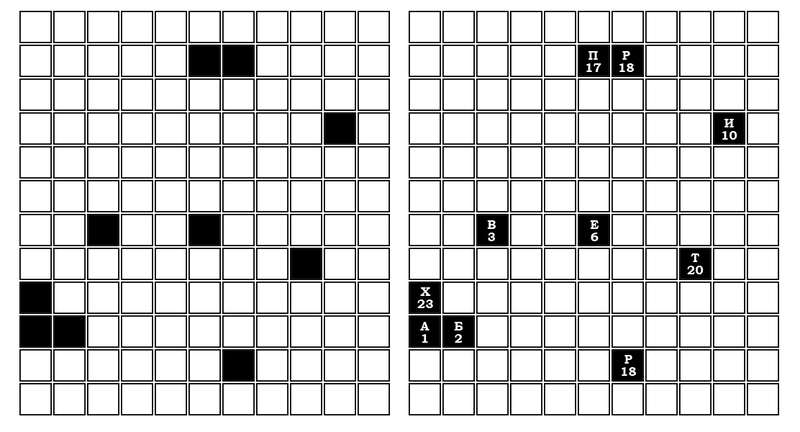
There are many options for solving the encrypted information. For example, in the sentences of the Russian language, the most common letters are A, E, I, O, T, B, C, L, U, I. So, ciphers with substitution of characters or other symbols are quickly figured out. And such a table of black and white squares, will introduce a person into a stupor.

And I think that this is still the most elementary type of information encryption. Let's try to complicate it.

And what if you reduce the size of the squares to 1px and remove the stroke of the squares? Then the picture will turn out to be something resembling a QR code.



Do you want to complicate the algorithm again? You can rotate our square by 90 degrees and get a completely different idea of ​​it, which will further mislead people trying to unravel it.



We will stop at this, but we will not finish. In the above lower case algorithm, only two colors were used, black and white, and what about all the others? They give us even more opportunities.

I hope we still remember that there are 33 letters in Russian? Recall some more elementary things that we need. 10 letters of the Russian alphabet vowels are: a, o, u, s, u, i, e, e, u, i. Consonants - 21 - is: b, c, d, d, f, f, z, k, l, m, n, n, p, c, t, f, x, c, h, w, w. And two letters without sounds: , .

To mark the colors let's take the 7 colors of the rainbow. "Every hunter wants to know where the pheasant sits" - well, how can it be without it?



Divide the vowels into two halves of 5 letters. Consonants to three halves of 7 letters each. And color the appropriate letters.

• Red color - a, o, u, s, e.
• Orange color - i, e, e, u, i.
• Yellow color - b, c, d, d, f, f, h.
• Green color - k, l, m, n, n, p, c.
• Blue color - t, f, x, c, h, w, y.
• Blue color - s.
• Purple - let's fill them with empty areas. Or it can be left for punctuation marks.

Take the same table of 33 three cells divided into 11 lines. And we will paint the cells by the same method described above. Let's write the phrase "Hi habr."



Thus, all our black and white cells became colored. What do these colors allow us to do?

As I wrote above, the color we can much more difficult to encrypt information. And think about how many colors have colors? And when repeating a letter, we can assign it a completely different shade. It all depends on your imagination and knowledge.

How else can colors be used when encrypting? Hmm ... Yes, a lot of ways. Take, for example, color circles. For those who do not know: The color wheel is a tool that helps to choose the most pleasant and harmonious colors among themselves. Mainly used and simplifies the work of designers.

Such color circles can be found on the Internet, or for example they are in the program CorelDRAW.

Suppose we take such a circle on the Internet:



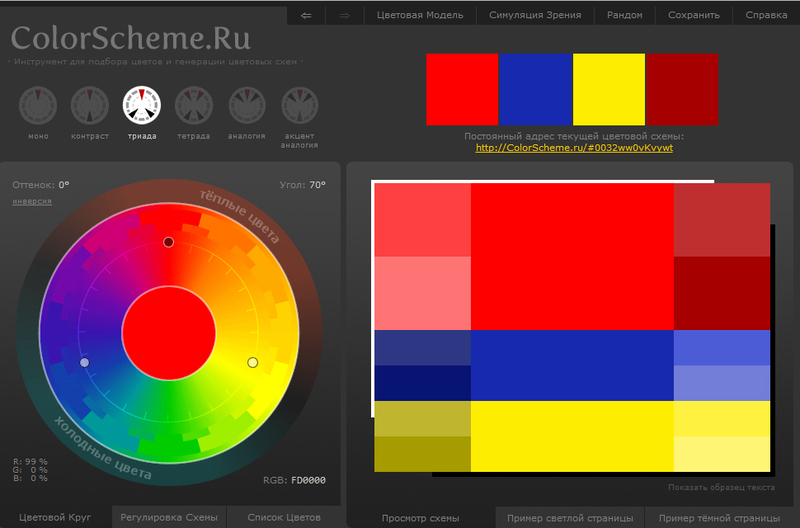
And for example, when repeating letters in a phrase or in a sentence, we will rotate the sliders of this circle by a certain number of degrees. Or put the main slider in the place of his friend, which will give us completely new colors.

It seems to me that with certain color encryption methods, we will be able to receive real works of art that carry secret messages and encrypted information.

I repeat that there may be many options. The question is only one and the most important. Is it possible to create a reverse encryption algorithm for your encrypted message and will it be simple to implement?

If the rules of this site allow you to do the following, then you can send various encryption options, invented by you, to my mail: ritear@mail.ru. And if you accumulate a large number of interesting options, I will write another article with different methods of presenting information in the form of a cipher. In order to facilitate my work, please indicate in the letter the topic “Own encryption methods”, and of course the author of the article, do you want many people to hear about you?

Let your comments be my judge.