Casual bot for casual game

Evaluating google + , accidentally stumbled upon a simple flash game - push the cubes of the same color, they burst, and we get points and profit. But instead of clicking on the cubes myself, I decided to write a bot that would do all this for me.

A bot for this long-suffering game already exists ( and not just one ), but I wanted to do not track the transfer protocols, tinkering someone else's and introduce my code, but try to implement pattern recognition and decision-making based on them, that is, some emulation of the real player's actions. No matane, only for fun . Implementation on .NET under habrokat.


')
The blocks in the game are static ( non-animated ) sprites, and with hard positioning. The easiest way would be to measure the position of each block by pixels, and then determine them by the manually created template. But it will not be so interesting and boring, especially since such a method will be strictly tied specifically to this game. Therefore, I decided to make a bot that will ( partly ) determine the position of the playing field and the elements on it.



So, first of all, you need to select all possible elements. In total, they turned out 5 pieces *. Cut out in the point, save to a folder. Next, you need to determine the width and height of the playing field, the number of elements placed on it horizontally and vertically.



These elements and need to search on the screen. In practice, the field begins where one of them meets for the first time. It is necessary to determine the position of the field only once - at the beginning of the game, so there is no reason to worry too much about the speed of this part. Pixel-by-pixel comparison is too long, and such accuracy is of no use to us, so we choose the most different points from each other in the sprites of the elements ( I got somewhere in the middle ). Then we get a screenshot of the screen and look for this pixel on it. If a pixel is found, then we check if the found pixel belongs to the desired element.



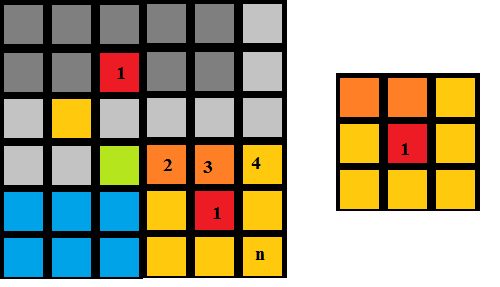
The first element found will indicate the initial boundary of the playing field. In order to shorten the search for this element, we do not remove the entire screen, but let the user determine the approximate area of ​​the playing field (I used the main form with transparency for this).

Further, it is still easier, we break the field into pieces, each of which we need to compare the existing block. To do this, we define the “average” color of each block and the average color of the “piece” of the field and compare them **.

C # code

//""  //detail -    . private Color getMidColor(Bitmap inpBit, int x, int y, int w, int h, int detail) { double r = 0, g = 0, b = 0; for (var ii = x; ii < x + w; ii += detail) for (var jj = y; jj < y + h; jj += detail) { var pix = inpBit.GetPixel(ii, jj); r += pix.R; g += pix.G; b += pix.B; } r /= (w * h / detail / detail);// :-( g /= (w * h / detail / detail); b /= (w * h / detail / detail); return Color.FromArgb((int)r, (int)g, (int)b); } //  //   //blcColors -  ""  . private int colorCompare(Color c) { int max=255; int cur = -1; int imax; for(var i=0;i<blcColors.Count;i++) { imax=Math.Abs(cR - blcColors[i].R) + Math.Abs(cG - blcColors[i].G) + Math.Abs(cB - blcColors[i].B) / 3; if (imax < max) { max=imax; cur = i; } } if (max > 50)//    return -1;//     return cur; } 

Then we create a matrix of blocks and look for the largest piece of contiguous blocks (depth) on it. The task is trivial, a bit similar to the search for a way out of the maze.

 //..... for (var i = 0; i < 10; i++) for (var j = 0; j < 9; j++) { if (nots[i, j])//    count[i, j] = //   "" searching(i, j, 0); // ""     if(count[i, j]>max) { x=i; y=j; max = count[i, j]; } } //..... //     private int searching(int i, int j, int c) { nots[i, j] = false; //    for (var di = -1; di <= 1; di++) for (var dj = -1; dj <= 1; dj++) if (di+i >= 0 && di+i < 10 && dj+j >= 0 && dj+j < 9) //   ? if (Math.Abs(di) != Math.Abs(dj)) //     ? if (cube[i, j] == cube[i + di, j + dj]) // ? if (nots[i + di, j + dj]) // ? { c = searching(i + di, j + dj, c+1); //  ! } return c; } } 

The shell and form code probably doesn't make sense to write: if you find the playing field on the screen, then start the timer (for example, a quarter of a second). When the timer is triggered, we determine the most "deep" block and click on it on the screen .

An example of the work of the bot. Moreover, at least the program spends 15-20 ms to recognize the blocks and make a decision in the sum, there is not much sense from this, because On my window, a flash drive and so produces a scant 10-20 fps, and with the removal of the video, and so does a slide show. Maximum my bot was able to fill 300k.


____
* In fact, they turned out to be 6. I found out about this only after I added the bot, because when I played (badly) myself, this block did not appear.
** It was possible to make a division into 2, 4 or more blocks, but here it was superfluous.