Geekly Articles each Day
📜 ⬆️ ⬇️

The simplest compression algorithms: RLE and LZ77

A long time ago, when I was still a naive schoolboy, I suddenly became terribly curious: how magically do the data in the archives take up less space? Riding my loyal dialup, I began to surf the Internet in search of an answer, and found many articles with a rather detailed description of the information I was interested in. But none of them then seemed easy to understand - the code listings seemed like a Chinese script, and attempts to understand unusual terminology and various formulas were not crowned with success.

Therefore, the purpose of this article is to give an idea of ​​the simplest compression algorithms for those who do not yet have the knowledge and experience to understand more professional literature, or whose profile is far from similar subjects. Those. I will tell you “on the fingers” about one of the simplest algorithms and give examples of their implementation without kilometer code listings.

Immediately I warn you that I will not consider the details of the implementation of the coding process and such nuances as an effective search for line entries. The article will concern only the algorithms themselves and the ways of presenting the result of their work.

RLE - compactness of uniformity


The RLE algorithm is probably the simplest of all: its essence lies in coding repeats. In other words, we take sequences of identical elements, and “collapse” them into “quantity / value” pairs. For example, a string like “AAAAAAAABCCCC” can be converted to an entry like “8 × A, B, 4 × C”. That, in general, is all you need to know about the algorithm.
')

Implementation example


Suppose we have a set of certain integer coefficients, which can take values ​​from 0 to 255. In a logical way, we came to the conclusion that it is reasonable to store this set as an array of bytes:
unsigned char data[] = { 0, 0, 0, 0, 0, 0, 4, 2, 0, 4, 4, 4, 4, 4, 4, 4, 80, 80, 80, 80, 0, 2, 2, 2, 2, 255, 255, 255, 255, 255, 0, 0 };


For many, it will be much more common to see this data as a hex dump:
0000: 00 00 00 00 00 00 04 02 00 04 04 04 04 04 04 04
0010: 50 50 50 50 00 02 02 02 02 FF FF FF FF FF 00 00

Thinking, we decided that it would be good to save space somehow compress such sets. To do this, we analyzed them and revealed a pattern: very often come across subsequences consisting of identical elements. Of course, RLE is the perfect fit for this!

We will encode our data using the newly acquired knowledge: 6 Ă— 0, 4, 2, 0, 7 Ă— 4, 4 Ă— 80, 0, 4 Ă— 2, 5 Ă— 255, 2 Ă— 0.

It's time to somehow present our result in a form understandable to a computer. For this, in the data stream, we must somehow separate the single bytes from the encoded chains. Since the entire range of byte values ​​is used by our data, then it will not be possible to simply select any ranges of values ​​for our goals.

There are at least two ways out of this situation:
  1. As an indicator of a compressed chain, select one value of a byte, and in case of a collision with real data, shield them. For example, if we use the value 255 for “official” purposes, then when meeting this value in the input data we will have to write “255, 255” and after the indicator use a maximum of 254.
  2. To structure the coded data, indicating the number of not only repeated, but subsequent subsequent single elements. Then we will know in advance where the data is.

The first method in our case does not seem effective, therefore, perhaps, we will resort to the second.

So, now we have two types of sequences: chains of single elements (like "4, 2, 0") and chains of identical elements (like "0, 0, 0, 0, 0, 0"). Let us single out one bit in the "service" bytes for the sequence type: 0 - single elements, 1 - the same. Take for this, say, the high bit of a byte.

In the remaining 7 bits, we will store the lengths of the sequences, i.e. The maximum length of the encoded sequence is 127 bytes. We could allocate for service needs, say, two bytes, but in our case such long sequences are extremely rare, so it’s easier and more economical to just break them up into shorter ones.

It turns out that we will write to the output stream first the length of the sequence, and then either one repeated value or a chain of non-repeatable elements of the specified length.

The first thing that should be evident - in this situation, we have a couple of unused values. There can be no sequences with zero length, so we can increase the maximum length to 128 bytes, subtracting one from the length when encoding and adding to decoding. Thus, we can encode lengths from 1 to 128 instead of lengths from 0 to 127.

The second thing to notice is that there are no sequences of identical elements of unit length. Therefore, we will subtract one more from the value of the length of such sequences, thereby increasing their maximum length to 129 (the maximum length of the chain of single elements is still equal to 128). Those. chains of identical elements can have length from 2 to 129.

We will encode our data again, but now in a form understandable for a computer. We will write service bytes as [T | L], where T is the type of the sequence, and L is the length. We will immediately take into account that we write the lengths in a modified form: at T = 0 we subtract one from L, at T = 1 - two.

[1 | 4] , 0, [0 | 2] , 4, 2, 0, [1 | 5] , 4, [1 | 2] , 80, [0 | 0] , 0, [1 | 2] , 2, [1 | 3] , 255, [1 | 0] , 0

Let's try to decode our result:


And now the last step: save the result as an array of bytes. For example, a pair [1 | 4] packed in byte will look like this:


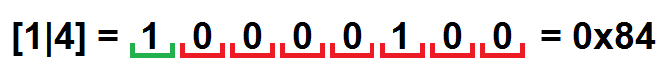
As a result, we obtain the following:
0000: 84 00 02 04 02 00 85 04 82 80 00 00 82 02 83 FF
0010: 80 00

So in this simple example of input data, we received from 32 bytes 18. Not a bad result, especially considering that it can be much better on longer chains.

Possible improvements


The efficiency of the algorithm depends not only on the algorithm itself, but also on the method of its implementation. Therefore, for different data it is possible to develop different variations of the coding and presentation of the encoded data. For example, when encoding images, you can make chains of variable length: select one bit for the indication of a long chain, and if it is set to one, then store the length in the next byte too. So we sacrifice the length of short chains (65 elements instead of 129), but we give the possibility to encode chains up to 16385 elements (2 14 + 2) in just three bytes!

Additional efficiency can be achieved by using heuristic coding methods. For example, we encode the following chain in our way: “ABBA”. We get “ [0 | 0] , A, [1 | 0] , B, [0 | 0] , A” - i.e. 4 bytes we turned into 6, inflated the original data as much as half as much! And the more such short alternating heterogeneous sequences, the more redundant data. If we take this into account, we could encode the result as “ [0 | 3] , A, B, B, A” - we would spend only one extra byte.

LZ77 - short in repetition


LZ77 is one of the most simple and well-known algorithms in the LZ family. Named in honor of its creators: Abraham Lempel (Abraham L empel) and Jacob Ziv (Jacob Z iv). Figures 77 in the title indicate the year 1977, in which an article was published describing this algorithm.

The basic idea is to encode the same sequence of elements. That is, if in the input data some chain of elements occurs more than once, then all its subsequent entries can be replaced by “links” to its first instance.

Like the rest of the algorithms of this family of families, LZ77 uses a dictionary in which sequences previously encountered are stored. For this, he applies the principle of so-called. “Sliding window”: an area always in front of the current coding position within which we can address links. This window is a dynamic dictionary for this algorithm - each element in it corresponds to two attributes: position in the window and length. Although in the physical sense, this is just a section of memory that we have already encoded.



Implementation example


Now let's try to code something. Let's generate for this some suitable line (I apologize in advance for its absurdity):

“The compression and the decompression leave an impression. Hahahahaha! ”

Here is what it will look like in memory (ANSI encoding):
0000: 54 68 65 20 63 6F 6D 70 72 65 73 73 69 6F 6E 20 The compression
0010: 61 6E 64 20 74 68 65 20 64 65 63 6F 6D 70 72 65 and the decompre
0020: 73 73 69 6F 6E 20 6C 65 61 76 65 20 61 6E 20 69 ssion leave an i
0030: 6D 70 72 65 73 73 69 6F 6E 2E 20 48 61 68 61 68 mpression. Hahah
0040: 61 68 61 68 61 21 ahaha!

We have not yet decided on the size of the window, but we agree that it is larger than the size of the encoded string. Let's try to find all duplicate chains of characters. Chain will be considered a sequence of characters longer than one. If the chain is part of a longer repeating chain, we will ignore it.

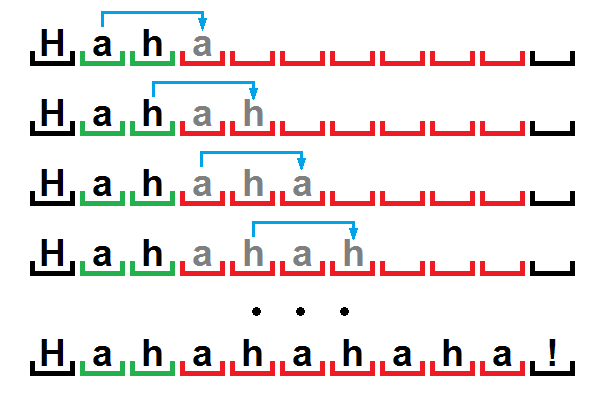
“The compression and t [he] de [compression] leave [an] i [mpression] . Hah [ahahaha] ! ”

For the sake of clarity, let’s look at the scheme where the correspondences of the repeated sequences and their first occurrences are visible:



Perhaps the only obscure point here is the sequence “Hahahahaha!”, Because the short string “ah” corresponds to the string of characters “ahahaha”. But there is nothing unusual here, we used some technique that allows the algorithm to sometimes work like the RLE described earlier.

The fact is that when unpacking, we will read the specified number of characters from the dictionary. And since the entire sequence is periodic, i.e. the data in it is repeated with a certain period, and the characters of the first period will be directly in front of the unpacking position, then we can recreate the entire chain by simply copying the characters of the previous period into the next one.


With this sorted out. Now let's replace the found repetitions with links in the dictionary. We will write the link in the format [P | L], where P is the position of the first occurrence of the string in the string, L is its length.

“The compression and t [22 | 3] de [5 | 12] leave [16 | 3] i [8 | 7] . Hah [61 | 7] ! ”

But do not forget that we are dealing with a sliding window. For a greater understanding that the links do not depend on the window size, let's replace the absolute positions by the difference between them and the current coding position.

“The compression and t [20 | 3] de [22 | 12] leave [28 | 3] i [42 | 7] . Hah [2 | 7] ! ”

Now we just need to take away P from the current coding position to get the absolute position in the string.

It's time to determine the size of the window and the maximum length of the coded phrase. Since we are dealing with text, it is rare when it will contain particularly long repeating sequences. So we will single out under their length, say, 4 bits - the limit of 15 characters at a time is enough for us.

But on the size of the window it already depends how deeply we will look for identical chains. Since we are dealing with small texts, it will be just right to supplement the number of bits we use to two bytes: we will address links in the range of 4096 bytes using 12 bits for this.

We know from experience with RLE that not all values ​​can be used. Obviously, a link can have a minimum value of 1, therefore, in order to address back in the range of 1..4096, we have to take one from the link when encoding, and add it back when decoding. The same with the lengths of the sequences: instead of 0..15 we will use the range of 2..17, since we do not work with zero lengths, and individual characters are not sequences.

So, we will present our coded text taking into account these amendments:

“The compression and t [19 | 1] de [21 | 10] leave [27 | 1] i [41 | 5] . Hah [1 | 5] ! ”

Now, again, we need to somehow separate the compressed chains from the rest of the data. The most common way is to reuse the structure and directly indicate where the compressed data is and where not. To do this, we divide the coded data into groups of eight elements (symbols or links), and before each of these groups we will insert a byte, where each bit corresponds to the type of element: 0 for a symbol and 1 for a link.

We divide into groups:

We compose the groups:

" {0,0,0,0,0,0,0,0} The comp {0,0,0,0,0,0,0,0,0} ression {0,0,0,0,0,1 , 0,0} and t [19 | 1] de {1,0,0,0,0,0,1,0} [21 | 10] leave [27 | 1] {0,1,0,0, 0,0,0,1} i [41 | 5] . Hah [1 | 5] {0} ! ”

Thus, if, while unpacking, we meet bit 0, then we simply read the character into the output stream, if bit 1, we read the link, and follow the link to read the sequence from the dictionary.

Now we just have to group the result into an array of bytes. We agree that we use bits and bytes in order from highest to lowest. Let's look at how links are packed into bytes in the example [19 | 1] :



As a result, our compressed stream will look like this:

0000: 00 54 68 65 20 63 6f 6d 70 00 72 65 73 73 69 6f #The comp # ressio
0010: 6e 20 04 61 6e 64 20 74 01 31 64 65 82 01 5a 6c n #and t ## de ### l
0020: 65 61 76 65 01 b1 20 41 69 02 97 2e 20 48 61 68 eave ## # i ##. Hah
0030: 00 15 00 21 00 00 00 00 00 00 00 00 00 00 00 00 ###!

Possible improvements


In principle, everything that has been described for RLE will be correct here. In particular, to demonstrate the benefits of the heuristic approach to encoding, consider the following example:

“The long goooooong. The loooooower bound.

Find sequences only for the word "loooooower":

“The long goooooong. The [lo] [ooooo] wer bound. "

To encode such a result, we need four bytes per link. However, it would be more economical to do this:

“The long goooooong. The l [oooooo] wer bound. "

Then we would spend one byte less.

Instead of conclusion


Despite its simplicity and, it would seem, not too much efficiency, these algorithms are still widely used in various fields of IT-sphere.

Their plus is simplicity and speed, and more complex and efficient algorithms can be based on their principles and their combinations.

Hopefully, the essence of these algorithms presented in this way will help someone to understand the basics and start looking towards more serious things.

Source: https://habr.com/ru/post/141827/

More articles:


All Articles