Introduction.

First of all, it is necessary to say what the Hamming Code is and why it is actually needed. Wikipedia gives the following definition:

Hamming codes are the most well-known and probably the first of self-controlling and self-correcting codes. They are constructed in relation to the binary number system.

In other words, it is an algorithm that allows you to encode any informational message in a certain way and after transmission (for example, over the network) to determine if some error occurred in this message (for example due to interference) and, if possible, to recover this message . Today, I will describe the simplest Hamming algorithm that can correct only one mistake.

It is also worth noting that there are more advanced modifications of this algorithm that allow you to detect (and if it is possible to correct) more errors.

Immediately it should be said that the Hamming Code consists of two parts. The first part encodes the original message, inserting into it in certain places the control bits (calculated in a special way). The second part receives the incoming message and re-calculates the control bits (according to the same algorithm as the first part). If all newly calculated check bits are the same as received, then the message is received without errors. Otherwise, an error message is displayed and, if possible, the error is corrected.
')

How it works.

In order to understand the operation of this algorithm, consider an example.

Training

Suppose we have a message “habr” that needs to be transmitted without errors. To do this, you first need to encode our message with the Hamming Code. We need to present it in binary form.



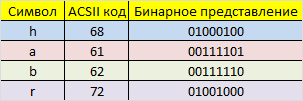
At this stage, it is necessary to determine the so-called length of the information word, that is, the length of the string of zeros and ones that we will encode. Suppose we have a word length of 16. So, we need to divide our original message (“habr”) into blocks of 16 bits, which we will then encode separately from each other. Since one character occupies 8 bits in memory, exactly two ASCII characters fit into one coded word. So, we got two binary strings of 16 bits each:

and

After that, the encoding process is parallelized, and the two parts of the message (“ha” and “br”) are encoded independently of each other. Consider how this is done on the example of the first part.
First of all, it is necessary to insert check bits. They are inserted in strictly defined places - these are positions with numbers equal to powers of two. In our case (with the length of the information word in 16 bits) these will be positions 1, 2, 4, 8, 16. Accordingly, we have 5 control bits (highlighted in red):

It was:


It became:


Thus, the length of the entire message increased by 5 bits. Before calculating the check bits themselves, we assigned them the value "0".

Calculation of check bits.

Now it is necessary to calculate the value of each control bit. The value of each control bit depends on the values ​​of the information bits (as unexpectedly), but not on all, but only on those that this control bits control. In order to understand which bits each control bit is responsible for, it is necessary to understand a very simple pattern: the control bit with the N number controls all subsequent N bits after every N bits, starting from the position N. Not very clear, but I think it will be from the picture clearer:

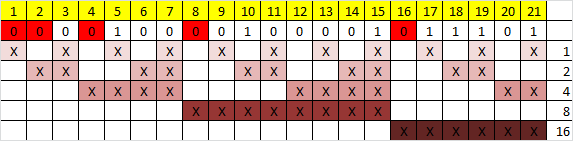
Here, the “X” denotes those bits that are controlled by the check bit, the number of which is to the right. That is, for example, bit number 12 is controlled by bits with numbers 4 and 8. It is clear that in order to know which bits control bit with number N, you just need to decompose N in powers of two.

But how to calculate the value of each control bit? This is done very simply: we take each check bit and see how many bits of units it controls, we get some integer number and, if it is even, then we set zero, otherwise we set one. That's all! Of course, it is possible and vice versa, if the number is even, then we set one, otherwise, we put 0. The main thing is that the algorithm is the same in the “coding” and “decoding” parts. (We will apply the first option).
Having calculated the check bits for our information word, we get the following:

and for the second part:


That's all! The first part of the algorithm is complete.

Decoding and correction of errors.

Now, let's say we received the message encoded by the first part of the algorithm, but it came to us with an error. For example, we got this (the 11th bit was transmitted incorrectly):

The whole second part of the algorithm is that it is necessary to re-calculate all the control bits (as in the first part) and compare them with the control bits that we received. So, counting the control bits with the wrong 11th bit, we get the following picture:

As we can see, the check bits numbered 1, 2, 8 do not coincide with the same check bits that we received. Now simply adding the position numbers of the wrong control bits (1 + 2 + 8 = 11) we get the position of the wrong bit. Now simply inverting it and discarding the control bits, we get the original message in its original form! We do the same thing with the second part of the message.

Conclusion

In this example, I took the length of the informational message exactly 16 bits, since it seems to me that it is the most optimal for considering the example (not too long and not too short), but of course you can take any length. Only it is necessary to take into account that in this simple version of the algorithm only one error can be corrected for one information word.

Note.

I was inspired to write this topic by the fact that I didn’t find articles on this topic on Habré (which I was extremely surprised with). Therefore, I decided to partly correct this situation and show as much as possible how this algorithm works. I deliberately did not give a single formula in order to try in my own words to convey the process of the algorithm using an example.

Sources.

1. Wikipedia
2. Calculating the Hamming Code