Restriction of optimizing methods in games with an opponent and without
This article is a short break from the cycle of articles on bio-computing:
From proteins to RNA , Mat. criteria How to reduce the number of turns the chain? How to evaluate the course of folding of single-stranded RNA?
In these articles, the task of folding RNA is presented in a new light - as the task of game theory. But traditionally, this problem is now solved with the use of various stochastic optimizing methods. And these include methods based on the Monte Carlo method, the annealing method, genetic algorithms, artificial neural networks, Q-learning, and all those that represent the problem as an energy surface in which extremes are sought.
It would seem that physics itself orders to use these methods in such tasks as folding RNA / proteins. Here we will see why this is very problematic.
')
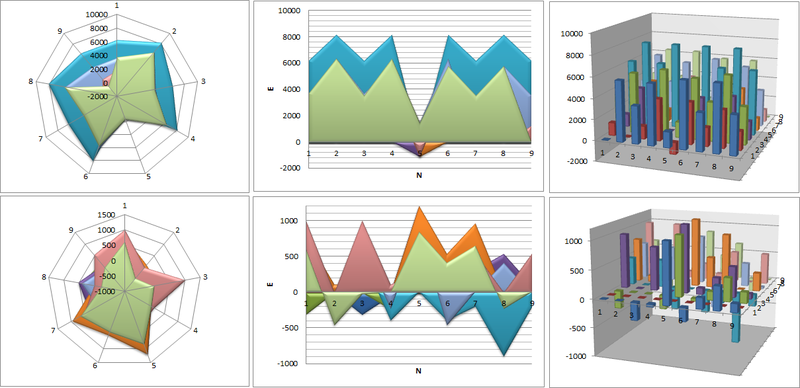
The basic idea is very simple indeed. Let's take the simplest of games with the opponent tic-tac-toe, and build an energy surface and its changes during the moves of the players. The figure shows the energy surface in the first row at the beginning of the game, in the second row after the move of the crosses to position 2 (positions 1 to 9, listing left to right, bottom to top).
And note, this is the simplest game, and what will happen in chess, but I’m generally silent about bio-computation :)
It only remains for me to ask : what will optimizing algorithms look for when each new move changes the energy surface in such a way that it becomes practically non-repeatable? Will there be even the slightest optimization compared to brute force?
From proteins to RNA , Mat. criteria How to reduce the number of turns the chain? How to evaluate the course of folding of single-stranded RNA?
In these articles, the task of folding RNA is presented in a new light - as the task of game theory. But traditionally, this problem is now solved with the use of various stochastic optimizing methods. And these include methods based on the Monte Carlo method, the annealing method, genetic algorithms, artificial neural networks, Q-learning, and all those that represent the problem as an energy surface in which extremes are sought.
It would seem that physics itself orders to use these methods in such tasks as folding RNA / proteins. Here we will see why this is very problematic.
')
The basic idea is very simple indeed. Let's take the simplest of games with the opponent tic-tac-toe, and build an energy surface and its changes during the moves of the players. The figure shows the energy surface in the first row at the beginning of the game, in the second row after the move of the crosses to position 2 (positions 1 to 9, listing left to right, bottom to top).

The figure on the right shows a 3-dimensional discrete surface that is formed. On the Y-axis - the Mini-Max energy estimate is displayed, on the Z-axis, the current player’s move position, and on the X-axis, the opponent’s move position. Each point on the surface shows what chances the opponent player has depending on the player’s move. The projections of this surface are in the figure in the center a side view, and on the left a top view.
We see that a move to position 5 increases the player’s chances (see side view). The move to other positions does not give visible advantages - the area in the top view is filled almost evenly. If the player puts the cross in position 2, then the energy surface will change significantly. Then, if the zero takes the position 5, then the most dangerous position for the crosses becomes 8. From the top view it is clear that if the central position of 5 is not played, then the chances of the players are not so uniform as at the beginning of the game. So setting to position 1, 3, 5, 7 expands the possibilities of zeros, and 4 greatly reduces.
And note, this is the simplest game, and what will happen in chess, but I’m generally silent about bio-computation :)
It only remains for me to ask : what will optimizing algorithms look for when each new move changes the energy surface in such a way that it becomes practically non-repeatable? Will there be even the slightest optimization compared to brute force?
Source: https://habr.com/ru/post/140470/
All Articles