Why does the Feistel network work? Explanation "on the fingers"

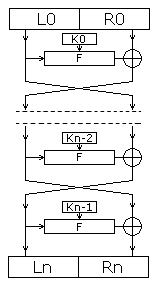
In the continuation of the article about blowfish, I would like to talk about its basis - the Feistel network . People "in the subject" have heard about it more than one hundred times - this network is used in the vast majority of block ciphers. But here you are, honestly, is something clear from the picture on the right? Well, let's say one way (encryption) is understandable, and back?
If not, then I ask under the mat


For a start, at least a quick run over the wikistat in order to understand in general terms what it is about

For simplicity, we will work with a block consisting of only two bytes. As Wikipedia says, it needs to be cut in half and name the left side L , and the right side R. Let it be so.
')
And so, we have two halves of the block, and the mysterious function F. Let's go

• The first thing we need to learn is that XOR (denoted by ⊕ ) is an involutive operation. Do not kick your feet, it just means that if you duplicate one number with another twice, then we will again get what we need. Those. A ⊕ B ⊕ B == A.
  It follows that we can build infinite chains A ⊕ B ⊕ C ⊕ D ⊕ ... and if we pereksory everything in the reverse order, we get A.
  For example, ((100 ⊕ 200) ⊕ 50) ⊕ 150 = 8. Hence, 8 ⊕ 150 ⊕ 50 ⊕ 200 = 100
• The second important point is that only one half of a block changes at a time.
• Now about the “black box” or the function F. In theory, the function F can be any made-up function (albeit a complex hash that returns 0 stupidly), because when we reverse everything (decrypt) everything in reverse order, then the second argument is always will be the same result of this function that was in the process of encryption. In practice, its creation is akin to art and does not give a 100% guarantee from new cryptanalysis methods.

How does this “same” work out?

Consider the example of three rounds of steps

Encryption

0) We have L and R some numbers. Let them be 100 and 200. and F , some function depending on L and the number of the round n. Suppose, for example, F will simply add them modulo 256 (so as not to crawl per byte). Those. F (L, n) = (L + n)% 256. (% is the remainder of the division)

Round One (n = 1)
1) Take R (200) and xorim it with the result of the function F (L, n), i.e. 200 ((100 + 1)% 256) we get 173 .
2) We put 173 in place of L, and in place of R, the previous value of L (100), i.e. swap R and result xor R with function F.

Round 2 (n = 2)
1) Now L = 173, R = 100. Xorim 100 c ((173 + 2)% 256), we get 203
2) Put 203 in place of L, and 173 in place of R.

Round 3 (n = 3)
1) L = 203, R = 173. Xorim 173 c (((203 + 3)% 256), we get 99
2) Since the last round, we change only R (so that later the permutation is not done)

After encryption, L = 203, R = 99.

Decryption

We go in the reverse order, the numbers of rounds go from 3 to 1

Round 1 (n = 3)
1) L = 203, R = 99. Xorim 99 s (((203 + 3)% 256) we get 173 . Familiar number?
2) Put 173 in place of L, 203 in place of R

Round 2 (n = 2)
1) L = 173, R = 203. Hence, 203 ((173 + 2)% 256) = 100 . Almost!
2) Change L = 100, R = 173

Round 3 (n = 1)
1) L = 100, R = 173. We consider R (permutation, as is the case with encryption, not needed) = 173 ((100 + 1)% 256) = 200 URAAAA !!!

L = 100, R = 200. As in a pharmacy)

That is, the whole Feistel network essentially boils down to the alternate row of both halves of the block with some calculated values ​​that are substituted in the reverse order during encryption.

And lastly, the java code that implements the algorithm described above.

public class BlockTest
{
private static int rounds = 3;
public void feist ( int [] a, boolean reverse)
{
int round = reverse? rounds: 1;
int l = a [0];
int r = a [1];
for ( int i = 0; i <rounds; i ++)
{
if (i <rounds - 1) // if not the last round
{
int t = l;
l = r ^ f (l, round);
r = t;
}
else // last round
{
r = r ^ f (l, round);
}
round + = reverse? -eleven;
}
a [0] = l;
a [1] = r;
}
private int f ( int b, int k)
{
return b + k;
}
public void test ()
{
int [] a = new int [2];
a [0] = 100;
a [1] = 200;
feist (a, false );
feist (a, true );
}
}

Hope you enjoyed it;)