Towards Skein: Blowfish is simple and straightforward.

“Sack-shaped outgrowths move away from the stomach of puffer fish. When danger arises, they are filled with water or air, which makes the fish look like a swollen ball.
with protruding spines. The spherical state makes the fish almost invulnerable. If, however, a large enough predator tries to swallow such a ball, then it gets stuck
in the throat of a predator who later dies "

Wikipedia, the free encyclopedia.

By the end of 1993, a very awkward situation arose in the world of cryptography. The DES symmetric encryption algorithm, with its weak 56-bit key, was close to a fiasco, and the existing
at that time, alternatives such as Khufu, REDOC II, IDEA were protected by patents
and are not available for free use. The RC2 and RC4 algorithms developed by RSA Security at that time also required a licensing procedure. And in general, the cryptography industry within government organizations and large corporations has been
turned towards the use of secret algorithms such as Skipjack.
')
There was a certain vacuum. An encryption algorithm was needed, more cryptographic than dying DES, and at the same time without any restrictions on the right to use it.

And he appeared.

In 1994, at the Fast Software Encryption seminar in Cambridge, and subsequently in the journal Lecture Notes in Computer Science (# 809, 1994), Bruce Schneier presented his block cipher algorithm, which was named Blowfish.

Distinctive features of this algorithm were a higher degree of cryptographic strength than the DES algorithm (including through the use of a variable key length, up to 448 bits), high encryption / decryption speed (due to the generation of replacement tables) and of course the possibility of its free use for any goals.

Bruce Schneier's original article from the archive in 1994:
Block Ciphers II, Bruce Schneier (bottom of page):
Description of a New Variable-Length Key, 64-bit Block Cipher (Blowfish). 191-204

Or in pdf format

Introduction

BlowFish is a 64-bit block cipher algorithm with a variable-length key. It was developed by a well-known specialist in the field of cryptography and information security, Bruce Schneier, in 1993.

In general, the algorithm consists of two stages - key expansion and encryption / decryption of the source data.



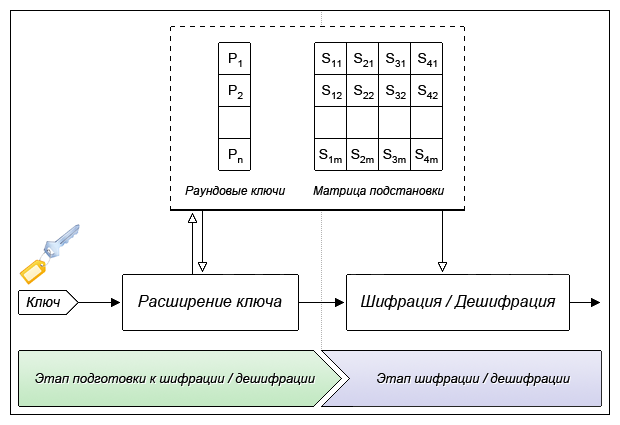
At the key expansion stage, the source key is converted into a matrix of round keys (P)
and a substitution matrix (S, Substitution-box) (or replacement), with a total of 4168 bytes. In all likelihood, this “extension” (from 448 bits to 4168 bytes) explains the choice of the name
Blowfish algorithm.

Data encryption, as well as the creation of a matrix of round keys and substitutions, occurs through the use of the Feistel network, which in turn consists of 16 rounds. Therefore, before we consider the steps of expanding the key and encrypting the data in detail, we need to decide what the Feistel network is.

In the process, we implement the software code of the encoder using the Blowfish algorithm in C ++. Ready-made implementations for high-level languages ​​(such as C / C ++ / Haskell / Perl / ...) are available on the page.
with the source code on the Bruce Schneier website.

Feistel Network

In 1971, the godfather of the DES standard, Horst Feistel (Horst Feistel), within the walls of IBM Corporation, developed two devices that implemented various encryption algorithms, then called the general name Lucifer. In one of these devices, he used a scheme that was later called the Feistel Network. This network is a certain repeatedly iterated (repetitive) structure, which is called a Feistel cell.



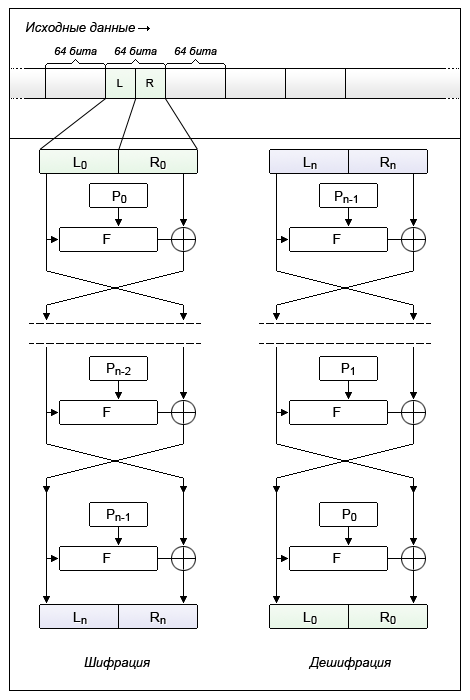
The principle of the network is quite simple:

1. The source data is divided into blocks of fixed length (usually a multiple of a power of two - 64 bits, 128 bits). If the length of the source data block is less than the length of the cipher, then the block is supplemented in some way known in advance.
   
   
2. The block is divided into two equal sub-blocks - the “left” L ₀ and the “right” R ₀ .
   In the case of 64-bit bit depth, two blocks with a length of 32 bits each.
   
   
3. The “left sub block” L _{0 is} modified by the iteration function F (L ₀ , P ₀ ) depending on the key P ₀ ,
   after which it is folded modulo 2 (XOR) with the “right subblock” R ₀ .
   
   
4. The result of the addition is assigned to the new left sub-block L ₁ , which becomes the left half of the input data for the next round, and the “left sub-block” L _{0 is} assigned without changes to the new right sub-block R ₁ , which becomes the right half.
   
   
5. This operation is repeated n-1 times, with the transition from one stage to another changing round keys (P ₀ , P ₁ , P ₂ , etc.), where n is the number of rounds for the algorithm used.

The decryption process is similar to the encryption process, except that round keys are used in the reverse order.

Let's go back to the Blowfish algorithm.

In general, the Blowfish encryption algorithm is a Feistel network, but with some features of generating and using round keys (P ₀ , P ₁ ...).

To begin with, let's assume that the iteration function F in the Blowfish algorithm is some kind of “black box” that accepts a 32-bit number (DWORD) at the input and outputs it.

In this case, 32-bit round keys Pn:

1. calculated according to some rule from the source key (up to 448 bits in length);
2. are not arguments for the iteration function F ;
3. directly stack modulo 2 (XOR) with a “left block”.
   The result of this operation is an incoming 32-bit argument for the function F.

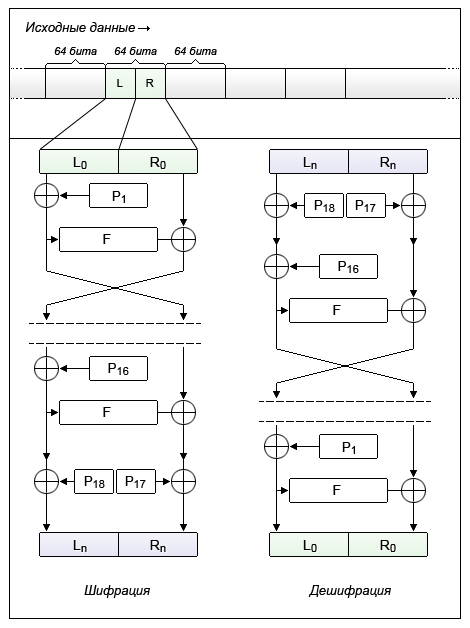
In the Blowfish algorithm, 16 rounds are performed during encryption (within the Feistel network), and the 17th and 18th keys are added to the left and right output blocks of the last round. This number of rounds was chosen because it determines the length of the possible key.

But here the attentive reader may ask: if 18 round keys are used, each of which has a length of 32 bits, then we end up with a key of 576 bits (18 keys × 32 bits). Why is the original key length in Blowfish originally limited to 448 bits?

The answer is simple - it is not limited. You can use keys up to 576 bits. But! The restriction was made based on the requirements for compliance with the security and cryptographic strength of the algorithm.

Let's implement the Feistel network for the Blowfish algorithm in C ++:

void swap(unsigned long *a, unsigned long *b) { unsigned long temp; if (a && b) { temp = *a, *a = *b, *b = temp; } } void blowfish_encrypt_block(blowfish_ctx *ctx, unsigned long *high, unsigned long *low) { int i; for (i = 0; i < 16; i++) { *high ^= ctx->p[i]; *low ^= F(ctx, *high); swap(low, high); } swap(low, high); *low ^= ctx->p[16]; *high ^= ctx->p[17]; } 

Key Expansion (Blow it up!)

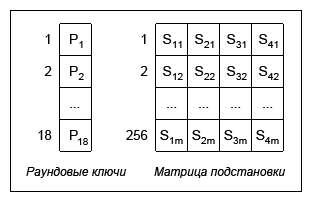
The preparatory stage of the Blowfish algorithm is the key expansion phase. During this stage, the matrix of round keys Pn and the substitution matrix are built - 4 S-Box replacement blocks (Substitution-boxes), each of which consists of 256 32-bit elements.



The elements of these matrices are encrypted (computed) using the Feistel network discussed above for the Blowfish algorithm. Thus, the Feistel network in the Blowfish algorithm is used:

• to encrypt / decrypt source data;
• to generate a matrix of round keys and a substitution matrix (i.e. a key extension).

The generated round key matrix and the substitution matrix are subsequently used.
in the process of encryption / decryption.

The key expansion process is processed.
18 × 32 (P ₁ , P ₂ ...) + 4 × 256 × 32 (S ₁ —S ₄ ) = 33344 bits or 4168 bytes of data.

When this is done (18 (Pn) + 4 × 256 (S ₁ —S ₄ )) / 2 = 521, a full iteration of the Feistel network.

All this is a very time-consuming operation, and that is why the Blowfish algorithm
It is not recommended to use where frequent change of key is required.

We describe the key expansion algorithm.

1. A “sincere number” is chosen (or else “Nothing up my sleeve number”). This is a number that does not initially contain any duplicate sequences and is known. This is done in order to show that the constant was chosen by the developers without pursuing any “vile” goals, for example, to create a loophole in the algorithm (backdoor).
   
   Blowfish usually uses the PI number as such a sincere number. We will not calculate the hexadecimal representation of the PI number, but use the ready-made solution: 8366 hexadecimal numbers of the mantissa for the PI number .
   
   
2. The value of the PI mantissa is filled with a matrix of round keys (FIXED_P) and a substitution matrix (FIXED_S):
   
   

    typedef struct _blowfish_ctx { unsigned long p[18]; unsigned long sbox[4][256]; } blowfish_ctx; const unsigned int FIXED_S[4][256] = { { 0xD1310BA6, 0x98DFB5AC, 0x2FFD72DB, 0xD01ADFB7, 0xB8E1AFED, 0x6A267E96, 0xBA7C9045, 0xF12C7F99, 0x24A19947, 0xB3916CF7, 0x0801F2E2, 0x858EFC16, 0x636920D8, 0x71574E69, 0xA458FEA3, 0xF4933D7E, 0x0D95748F, 0x728EB658, 0x718BCD58, 0x82154AEE, 0x7B54A41D, 0xC25A59B5, 0x9C30D539, 0x2AF26013, ....        .... 0xB74E6132, 0xCE77E25B, 0x578FDFE3, 0x3AC372E6 } }; const unsigned long FIXED_P[] = { 0x243F6A88, 0x85A308D3, 0x13198A2E, 0x03707344, 0xA4093822, 0x299F31D0, 0x082EFA98, 0xEC4E6C89, 0x452821E6, 0x38D01377, 0xBE5466CF, 0x34E90C6C, 0xC0AC29B7, 0xC97C50DD, 0x3F84D5B5, 0xB5470917, 0x9216D5D9, 0x8979FB1B }; 

   
   
   
3. The value of each round key Pn (P ₁ , P ₂ ...) is added modulo 2 (XOR) with the corresponding elements of the source key K. For example, the XOR round key P ₁ is performed
   with the first 32 bits of the original key K, P ₂ with the second 32 bits of the original key K, and so on. If the source key K is shorter than the length of all round keys (576 bits), then it concatenates itself
   with you: KK, KKK and so on.
   
   

    for(i = 0, k = 0; i < 18; i++) { for(j = 0, long_key = 0; j < 4; j++, k++) { long_key = (long_key << 8) | key[k % key_len]; } ctx->p[i] ^= long_key; } 

   
   
   
4. Next, we need to encrypt (calculate new values) the elements of the matrix of round keys and the substitution matrix. To do this, we will use the Blowfish Feistel network algorithm that we have implemented.
   
   
   1. Using the current round keys P ₁ —P ₁₈ and the S ₁ —S ₄ permutation matrixes (where exactly the permutation matrices are used will be described below), we encrypt the 64-bit zero sequence: 0x00000000 0x00000000, and write the result in P ₁ and P ₂ .
      
      
   2. P ₁ and P ₂ are encrypted with modified values ​​of round keys and substitution matrices, the result is written to P ₃ and P _4, respectively.
      
      
   3. Encryption continues until all round keys P ₁ —P ₁₈ and the elements of the permutation matrices S ₁ –S _{4 are} changed.
      
      Those. ultimately, we need to obtain the result of the calculation according to the Feistel network scheme of the Blowfish algorithm for (18 Pn + 4 × 256 (S ₁ —S ₄ )) / 2 = 521 iterations. We divided by 2, because for each iteration we calculate two new values ​​for the elements of the matrix of round keys or the matrix of substitutions.
   
   
   

    for (i = 0, k = 0, l = 0; i < 18; i++) { blowfish_encrypt_block(ctx, (unsigned long*)&k, (unsigned long*)&l); ctx->p[i] = k; ctx->p[++i] = l; } for (i = 0; i < 4; i++) { for (j = 0; j < 256; j++) { blowfish_encrypt_block(ctx, (unsigned long*)&k, (unsigned long*)&l); ctx->sbox[i][j] = k; ctx->sbox[i][++j] = l; } } 

   
   

At this point, the preparatory stage of the Blowfish algorithm — the key expansion — is completed. But before considering the stage of encryption / decryption, let’s still reveal our “black box” - the F function, which is executed at each round within iterations of the Feistel network for the Blowfish algorithm.

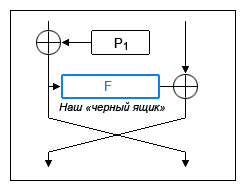
Iteration function (round)

The function of a round or iteration (since it is common to the entire Feistel network used) is very simple and uses only a few logical operations on the permutation matrix. Initially, while developing Lucifer, Horst Feistel even suggested using electronic substitution for a matrix with a simple linear circuit.



So:

1. The incoming 32-bit block is divided into four 8-bit blocks, let's call them X ₁ , X ₂ , X ₃ , X ₄
   (see picture above).
   
   
2. Each of which is an index of the array of the replacement table S ₁ —S ₄ .
3. S ₁ [X ₁ ] and S ₂ [X ₂ ] values ​​are added modulo 2 ³² , then the result is added
   modulo 2 (XOR) with S ₃ [X ₃ ] and, finally, add up with S ₄ [X ₄ ] again modulo 2 ³² .
4. The result of the calculation will be the value of the function F (X ₁ —X ₄ ).

Formula function:


Everything is extremely simple. The function uses the S ₁ —S ₄ permutation matrix to linearly translate the incoming 32 bits of data into a value from the substitution matrix. And the values ​​themselves
in matrices, substitutions are calculated at the key expansion stage that we considered earlier.

Implementing a function in C ++:

 unsigned long F(blowfish_ctx *ctx, unsigned long x) { return ((ctx->sbox[0][(x >> 24) & 0xFF] + ctx->sbox[1][(x >> 16) & 0xFF]) ^ ctx->sbox[2][(x >> 8) & 0xFF]) + ctx->sbox[3][(x) & 0xFF]; } 

And now let's move on to the actual process of encrypting the source data.

Encryption / decryption of source data

Surprise! In fact, we have already considered the algorithm for encrypting and decrypting source data. The thing is that, as we noticed at the very beginning, data encryption / decryption, and the creation of the aforementioned matrix of round keys and a substitution matrix, occurs with the help of the considered Feistel network for the Blowfish algorithm.

Those. in our software implementation, the entire process of encrypting the source data is built by analogy with the encryption process at the key expansion stage. Those. is an iterative execution of the blowfish_encrypt_block function (implementation of a Feistel network) over every 64 bits of source data. The round keys P (P ₁ , P ₂ , & hellip) and the substitution matrices S ₁ —S ₄ are the input parameters for the Feistel network and the F function, respectively, within this network.



In summary, if we summarize the encryption or decryption algorithm in the Blowfish algorithm,
then we get the following steps:

1. We select an array of 18 elements for the round keys of the Feistel network and 4 substitution matrices of 256 elements each.
   
   
2. Fill the selected array with the value of the PI mantissa.
   
   
3. Make an iterative XOR: Pi = Pi XOR Ki (where Pi is the round key and Ki is the original key).
   
   
4. We encrypt round keys and substitution matrices using a Feistel network (the substitution matrix is ​​used as an input parameter for the function within the network; the round keys within the network are taken from the matrix of round keys).
   
   
5. We encrypt / decrypt 64-bit input data blocks also using a Feistel network.
   
   

It's simple.

Summary

Dear readers. To be able to describe complex things in simple words is very difficult.

Before you start writing this text, I tried to put myself in the developer’s place,
who wants to try to study the considered Blowfish algorithm.

So, I set a goal to find in the network a document describing this algorithm with sufficient, for its understanding, completeness. In the end, of course, I got on the pages of Wikipedia, and on the forums, and even on different term papers. But reading the description presented there often raised more questions than answers.

All this confirmed me in the opinion that a simple and at the same time detailed description with examples would be useful and in demand. Therefore, for my part, I tried to “arrange everything on the shelves” as far as possible. But how well I did it - to judge you.

Thank.
Yours sincerely, AB

ps It is planned to continue ...